Calculus Homework: Cable Cost Minimization and Vector Calculations
VerifiedAdded on 2023/06/13
|7
|1542
|211
Homework Assignment
AI Summary
This assignment provides solutions to calculus problems involving cost optimization and vector analysis. The first question focuses on minimizing the cost of laying cables, considering different costs for cables on land and underwater, and uses calculus to determine the optimal length of cable to lay on land versus underwater to minimize total cost. It includes calculations of cable lengths, costs for different configurations, and a table showing the cost variations with changing distances. The second question involves solving a system of equations using Crammer’s rule to find the coefficients of a polynomial. The third question deals with vector analysis, determining the position vectors of points, the angle between them, relative positions, magnitude, and unit vectors. Desklib offers this solution and many other solved assignments for students.

Solution to question 1:
Cables on land, cost: $2700/km
Cables under water, cost: $3600/km
(a)Cable length from I to E
IE¿ √(PE^2+IP^2)
=√422 +252
=48.877 km.
Cables laid under water hence total cost of connection:
¿ ( 48.877 km∗$ 3600 )
1 km
=$175958.63
(b) Cable length on land = 42 km
Cost, Cl= 42 km∗$ 2700
1 km
Cl = $ 113400
Cable length thro’ sea = 25 km
Cost, Cs = 25 km∗$ 3600
1 km
Cs = $90,000
Total cost of connection = Cs + Cl = $90000 + 113400
= $203400
(c) length AE = (42-x) km
Length AI = √ 252 + x2
= ( √625+ x2 ) km
But AI is in the Sea while AE is on land
Connection cost = ((42- x ¿ km∗$ 2700 ¿/1 km+¿
1
Cables on land, cost: $2700/km
Cables under water, cost: $3600/km
(a)Cable length from I to E
IE¿ √(PE^2+IP^2)
=√422 +252
=48.877 km.
Cables laid under water hence total cost of connection:
¿ ( 48.877 km∗$ 3600 )
1 km
=$175958.63
(b) Cable length on land = 42 km
Cost, Cl= 42 km∗$ 2700
1 km
Cl = $ 113400
Cable length thro’ sea = 25 km
Cost, Cs = 25 km∗$ 3600
1 km
Cs = $90,000
Total cost of connection = Cs + Cl = $90000 + 113400
= $203400
(c) length AE = (42-x) km
Length AI = √ 252 + x2
= ( √625+ x2 ) km
But AI is in the Sea while AE is on land
Connection cost = ((42- x ¿ km∗$ 2700 ¿/1 km+¿
1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
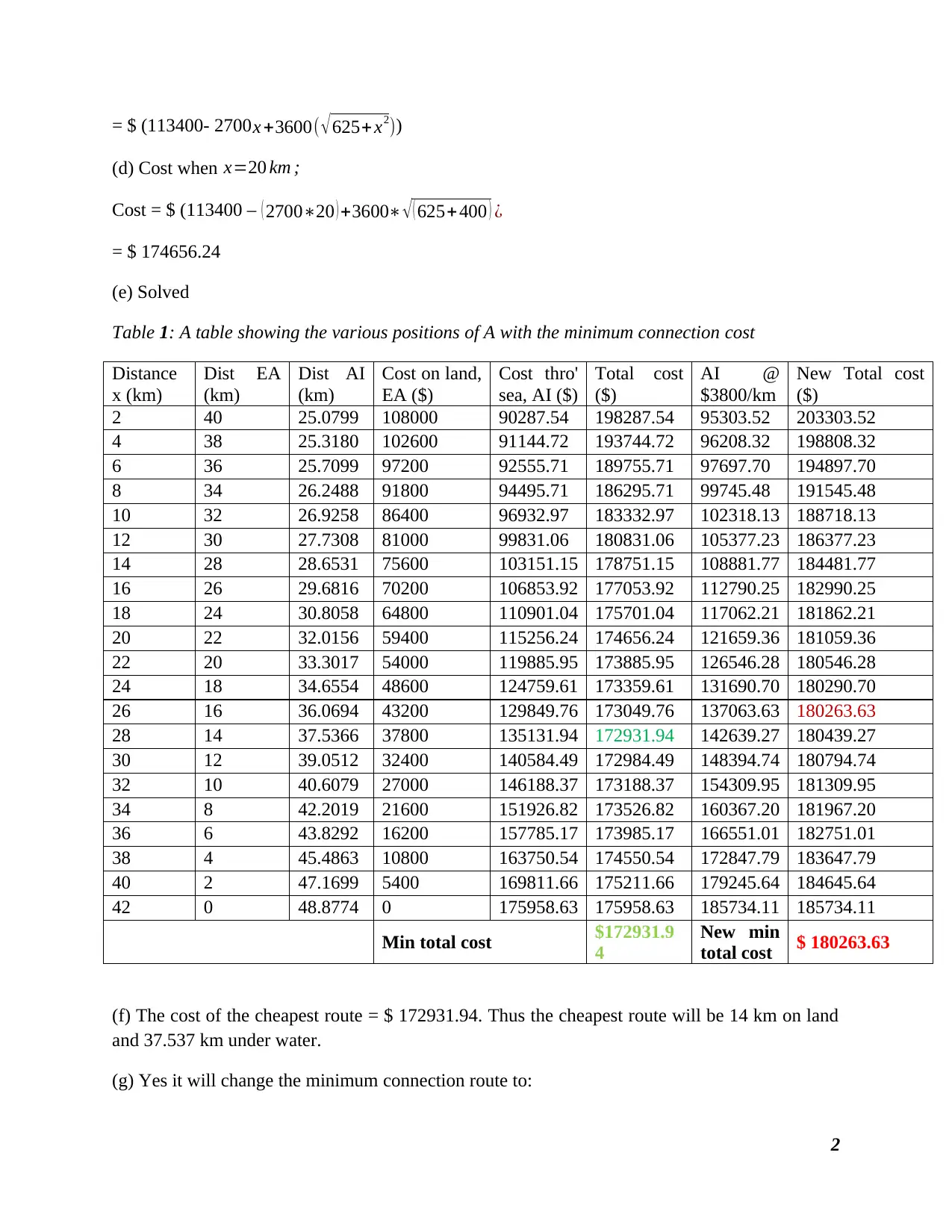
= $ (113400- 2700x +3600( √625+x2))
(d) Cost when x=20 km ;
Cost = $ (113400 – ( 2700∗20 ) +3600∗ √ ( 625+ 400 ) ¿
= $ 174656.24
(e) Solved
Table 1: A table showing the various positions of A with the minimum connection cost
Distance
x (km)
Dist EA
(km)
Dist AI
(km)
Cost on land,
EA ($)
Cost thro'
sea, AI ($)
Total cost
($)
AI @
$3800/km
New Total cost
($)
2 40 25.0799 108000 90287.54 198287.54 95303.52 203303.52
4 38 25.3180 102600 91144.72 193744.72 96208.32 198808.32
6 36 25.7099 97200 92555.71 189755.71 97697.70 194897.70
8 34 26.2488 91800 94495.71 186295.71 99745.48 191545.48
10 32 26.9258 86400 96932.97 183332.97 102318.13 188718.13
12 30 27.7308 81000 99831.06 180831.06 105377.23 186377.23
14 28 28.6531 75600 103151.15 178751.15 108881.77 184481.77
16 26 29.6816 70200 106853.92 177053.92 112790.25 182990.25
18 24 30.8058 64800 110901.04 175701.04 117062.21 181862.21
20 22 32.0156 59400 115256.24 174656.24 121659.36 181059.36
22 20 33.3017 54000 119885.95 173885.95 126546.28 180546.28
24 18 34.6554 48600 124759.61 173359.61 131690.70 180290.70
26 16 36.0694 43200 129849.76 173049.76 137063.63 180263.63
28 14 37.5366 37800 135131.94 172931.94 142639.27 180439.27
30 12 39.0512 32400 140584.49 172984.49 148394.74 180794.74
32 10 40.6079 27000 146188.37 173188.37 154309.95 181309.95
34 8 42.2019 21600 151926.82 173526.82 160367.20 181967.20
36 6 43.8292 16200 157785.17 173985.17 166551.01 182751.01
38 4 45.4863 10800 163750.54 174550.54 172847.79 183647.79
40 2 47.1699 5400 169811.66 175211.66 179245.64 184645.64
42 0 48.8774 0 175958.63 175958.63 185734.11 185734.11
Min total cost $172931.9
4
New min
total cost $ 180263.63
(f) The cost of the cheapest route = $ 172931.94. Thus the cheapest route will be 14 km on land
and 37.537 km under water.
(g) Yes it will change the minimum connection route to:
2
(d) Cost when x=20 km ;
Cost = $ (113400 – ( 2700∗20 ) +3600∗ √ ( 625+ 400 ) ¿
= $ 174656.24
(e) Solved
Table 1: A table showing the various positions of A with the minimum connection cost
Distance
x (km)
Dist EA
(km)
Dist AI
(km)
Cost on land,
EA ($)
Cost thro'
sea, AI ($)
Total cost
($)
AI @
$3800/km
New Total cost
($)
2 40 25.0799 108000 90287.54 198287.54 95303.52 203303.52
4 38 25.3180 102600 91144.72 193744.72 96208.32 198808.32
6 36 25.7099 97200 92555.71 189755.71 97697.70 194897.70
8 34 26.2488 91800 94495.71 186295.71 99745.48 191545.48
10 32 26.9258 86400 96932.97 183332.97 102318.13 188718.13
12 30 27.7308 81000 99831.06 180831.06 105377.23 186377.23
14 28 28.6531 75600 103151.15 178751.15 108881.77 184481.77
16 26 29.6816 70200 106853.92 177053.92 112790.25 182990.25
18 24 30.8058 64800 110901.04 175701.04 117062.21 181862.21
20 22 32.0156 59400 115256.24 174656.24 121659.36 181059.36
22 20 33.3017 54000 119885.95 173885.95 126546.28 180546.28
24 18 34.6554 48600 124759.61 173359.61 131690.70 180290.70
26 16 36.0694 43200 129849.76 173049.76 137063.63 180263.63
28 14 37.5366 37800 135131.94 172931.94 142639.27 180439.27
30 12 39.0512 32400 140584.49 172984.49 148394.74 180794.74
32 10 40.6079 27000 146188.37 173188.37 154309.95 181309.95
34 8 42.2019 21600 151926.82 173526.82 160367.20 181967.20
36 6 43.8292 16200 157785.17 173985.17 166551.01 182751.01
38 4 45.4863 10800 163750.54 174550.54 172847.79 183647.79
40 2 47.1699 5400 169811.66 175211.66 179245.64 184645.64
42 0 48.8774 0 175958.63 175958.63 185734.11 185734.11
Min total cost $172931.9
4
New min
total cost $ 180263.63
(f) The cost of the cheapest route = $ 172931.94. Thus the cheapest route will be 14 km on land
and 37.537 km under water.
(g) Yes it will change the minimum connection route to:
2

16 km on land and 36.07 km under water with a new minimum cost of $180263.63
Solution to question 2.
@ y=27.5, x=0
27.5 = A + D + E
@ y=8.2, x=25
8.2 = (1.389E-11)A + 25B + 0.4226C + 0.90631D + E
@ y=13 , x=10
13 = (4.54E-05)A + 10B + 0.17365C + 0.98481D + E
@ y=15 , x=15
15 = (3.059E-07) + 15B + 0.2588C + 0.9659D + E
@ y=16 , x=16
16 = 0.006737A + 5B + 0.08715C + 0.9962D + E
Forming a matrix of these equations:
| 1
4.4 × 10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|(A ,B, C) = (27.5, 8.2, 13, 16, 15)
Applying Crammer’s rule: (Thomas & Finney, 1988)
A=
|27.5
8.2
13
16
15
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|
| 1
4.4 ×10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|=29.67
3
Solution to question 2.
@ y=27.5, x=0
27.5 = A + D + E
@ y=8.2, x=25
8.2 = (1.389E-11)A + 25B + 0.4226C + 0.90631D + E
@ y=13 , x=10
13 = (4.54E-05)A + 10B + 0.17365C + 0.98481D + E
@ y=15 , x=15
15 = (3.059E-07) + 15B + 0.2588C + 0.9659D + E
@ y=16 , x=16
16 = 0.006737A + 5B + 0.08715C + 0.9962D + E
Forming a matrix of these equations:
| 1
4.4 × 10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|(A ,B, C) = (27.5, 8.2, 13, 16, 15)
Applying Crammer’s rule: (Thomas & Finney, 1988)
A=
|27.5
8.2
13
16
15
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|
| 1
4.4 ×10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|=29.67
3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
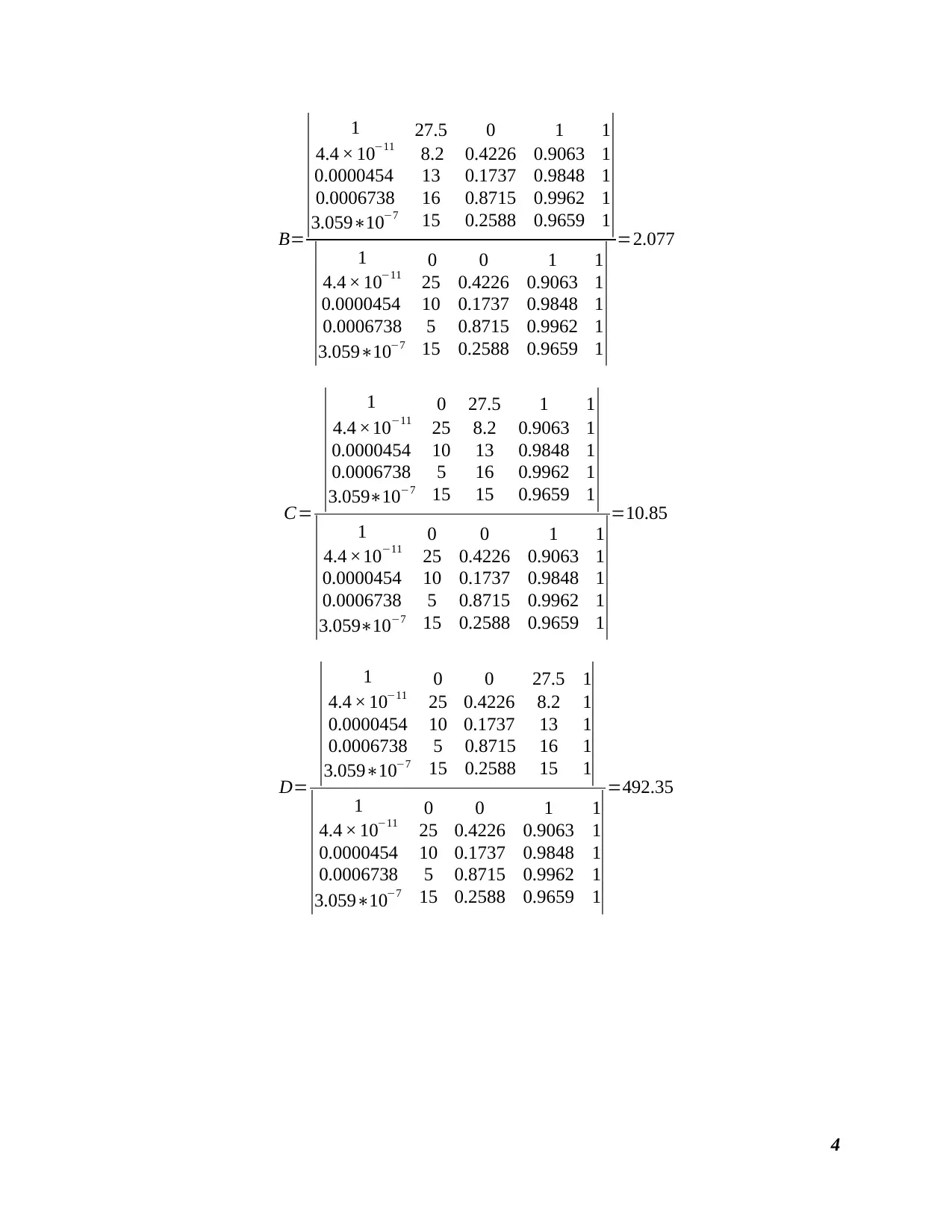
B=
| 1
4.4 × 10−11
0.0000454
0.0006738
3.059∗10−7
27.5
8.2
13
16
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|
| 1
4.4 × 10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
| =2.077
C=
| 1
4.4 ×10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
27.5
8.2
13
16
15
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|
| 1
4.4 ×10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|
=10.85
D=
| 1
4.4 × 10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
27.5
8.2
13
16
15
1
1
1
1
1
|
| 1
4.4 × 10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
| =492.35
4
| 1
4.4 × 10−11
0.0000454
0.0006738
3.059∗10−7
27.5
8.2
13
16
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|
| 1
4.4 × 10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
| =2.077
C=
| 1
4.4 ×10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
27.5
8.2
13
16
15
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|
| 1
4.4 ×10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
|
=10.85
D=
| 1
4.4 × 10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
27.5
8.2
13
16
15
1
1
1
1
1
|
| 1
4.4 × 10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
| =492.35
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

E=
| 1
4.4 ×10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
27.5
8.2
13
16
15 |
| 1
4.4 ×10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
| =−494.52
Solutions to question 3
(a) Shed: Built on 12 m above the ground level.
5 m high
Let the coordinates of the base of the shed be (4.26, 27.54) along the x-y plan.
Distance from ground level to top of shed = 12 m + 5 m = 17 m
Thus coordinates of point S with respect to origin (0,0,0) is given by:⃗
OS = { S }− { O }=
( 4260
27540
17 )−¿ (0
0
0 ) = ( 4260
27540
17 )
Thus point S is 4260 i + 27540 j + 17 k
(b) Lookout tower: On top of a hill, 110m above ground level.
10 m high.
Let the X-Y coordinate of T be (13.89, 4.4)
Distance from ground level to top of tower T = 110 m + 120 m
Thus coordinate of tower is T (13890, 4400, 120)
The position vector of point T with respect to origin O (0,0,0) is given by:⃗
OT = { T } − {O }= ( 13890
4400
120 )− ( 0
0
0 )= ( 13890
4400
120 )
Thus the position vector of T is 13890 I + 4400 j + 120 K.
5
| 1
4.4 ×10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
27.5
8.2
13
16
15 |
| 1
4.4 ×10−11
0.0000454
0.0006738
3.059∗10−7
0
25
10
5
15
0
0.4226
0.1737
0.8715
0.2588
1
0.9063
0.9848
0.9962
0.9659
1
1
1
1
1
| =−494.52
Solutions to question 3
(a) Shed: Built on 12 m above the ground level.
5 m high
Let the coordinates of the base of the shed be (4.26, 27.54) along the x-y plan.
Distance from ground level to top of shed = 12 m + 5 m = 17 m
Thus coordinates of point S with respect to origin (0,0,0) is given by:⃗
OS = { S }− { O }=
( 4260
27540
17 )−¿ (0
0
0 ) = ( 4260
27540
17 )
Thus point S is 4260 i + 27540 j + 17 k
(b) Lookout tower: On top of a hill, 110m above ground level.
10 m high.
Let the X-Y coordinate of T be (13.89, 4.4)
Distance from ground level to top of tower T = 110 m + 120 m
Thus coordinate of tower is T (13890, 4400, 120)
The position vector of point T with respect to origin O (0,0,0) is given by:⃗
OT = { T } − {O }= ( 13890
4400
120 )− ( 0
0
0 )= ( 13890
4400
120 )
Thus the position vector of T is 13890 I + 4400 j + 120 K.
5

(c) Angle between the two points S and T
Let the angle be .
Cos = a . b
|a||b| CITATION Sal95 \l 1033 (Salas & Holle, 1995)
a = ( 42602+ 275402+ 172 )2
=27867.53 m.
b = ( 138902 + 44002+1202 )
2
=14570.74 m .⃗
S .⃗ T = (13890
4400
120 ). ( 4260
27540
17 )=180349440
Therefore
cosθ= 180349440
27867.53 ×14570.74 =0.444155
θ=63.630
(d) Vector⃗
ST =⃗ T −⃗ S= (13890
4400
120 )− ( 4260
27540
120 )=
( 9630
−23140
103 )
Relative position of T from S = 9630 i – 23140 j + 103 k
(e) Magnitude of vector ST:
|⃗ST |= √ ( 9630 )2 + (−23140 )2 + ( 103 )2 ≈ 25.06 km
(f) Unit vector for direction ST
U =⃗ ST
|⃗ST |
ST = (9630, -23140, 103)
|ST |=25064.06 m
U = ( 0.3842 ,−0.9232, 4.1095∗10−3 )
(g) Unit vector perpendicular to both position vectors T and S
6
Let the angle be .
Cos = a . b
|a||b| CITATION Sal95 \l 1033 (Salas & Holle, 1995)
a = ( 42602+ 275402+ 172 )2
=27867.53 m.
b = ( 138902 + 44002+1202 )
2
=14570.74 m .⃗
S .⃗ T = (13890
4400
120 ). ( 4260
27540
17 )=180349440
Therefore
cosθ= 180349440
27867.53 ×14570.74 =0.444155
θ=63.630
(d) Vector⃗
ST =⃗ T −⃗ S= (13890
4400
120 )− ( 4260
27540
120 )=
( 9630
−23140
103 )
Relative position of T from S = 9630 i – 23140 j + 103 k
(e) Magnitude of vector ST:
|⃗ST |= √ ( 9630 )2 + (−23140 )2 + ( 103 )2 ≈ 25.06 km
(f) Unit vector for direction ST
U =⃗ ST
|⃗ST |
ST = (9630, -23140, 103)
|ST |=25064.06 m
U = ( 0.3842 ,−0.9232, 4.1095∗10−3 )
(g) Unit vector perpendicular to both position vectors T and S
6
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Cross product of OT and OS⃗
Q=T × S=
[ i j k
13890 4400 120
4260 27540 17 ]
Q = −3230000 i−275070 j+363786600 k
Unit vector U is given by
U =⃗ Q
|⃗Q|
|⃗Q|√ ( −3230000 ) 2 + ( −275070 ) 2 + ( 363786600 ) 2=363801043 m
U = ( −3230000 ,−275070 ,363786600 )
3638001043
Hence U = (−0.008878 ,−0.0007561 , 1 )=−0.008878 i – 0.0007561 j +k
REFERENCES
Salas, S. J., & Holle, E. (1995). Calculus: One & Several Variables. Wiley Publishers.
Thomas, & Finney. (1988). Calculus and Analytic Geometry. Addison Wisley.
7
Q=T × S=
[ i j k
13890 4400 120
4260 27540 17 ]
Q = −3230000 i−275070 j+363786600 k
Unit vector U is given by
U =⃗ Q
|⃗Q|
|⃗Q|√ ( −3230000 ) 2 + ( −275070 ) 2 + ( 363786600 ) 2=363801043 m
U = ( −3230000 ,−275070 ,363786600 )
3638001043
Hence U = (−0.008878 ,−0.0007561 , 1 )=−0.008878 i – 0.0007561 j +k
REFERENCES
Salas, S. J., & Holle, E. (1995). Calculus: One & Several Variables. Wiley Publishers.
Thomas, & Finney. (1988). Calculus and Analytic Geometry. Addison Wisley.
7
1 out of 7
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.

