Calculus Assignment Solution: Construction Tasks 1-4, Semester 1

This document presents a comprehensive solution to a calculus assignment designed for construction applications. The assignment is divided into four tasks, each addressing different aspects of calculus. Task 1 focuses on calculating bending moments, the lowest point of a suspension cable, and locations where voltage curves equal zero. Task 2 involves calculating the center of gravity of a flood defense wall profile and the deflection of a cantilevered beam. Task 3 applies Newton's law of cooling to determine initial temperatures and rates of change. Task 4 covers maxima and minima points for a road layout, calculating the maximum volume of a planter box, finding maximum and minimum voltage values, and analyzing vehicle flow rates over time. The solutions utilize calculus methods such as differentiation and integration to solve practical construction problems. The document provides detailed steps and calculations for each problem.

Calculus
(Mathematics for
Construction)

TASK 1
(i) The project has a series of double cantilevered beams with the Bending Moment equation
detailed below
BM = ax2 -bx +c
For your delegate student number and the details given on sheet 1 calculate the point of
maximum bending using calculus
Solution: The data given for different values of a, b and c as per number of students are given
below:-
For Student 8: a)25 b) 190.0338 c) 205.2365
So, the point of bending can be calculated by solving quadratic equation as –
25x2 -190.0338x +205.2365
Using, Calculus method : x = -b ± √b2 - 4ac ÷ 2a
x = (190.0338 ± √ (190.0338)2 - 4* 25 * 205.2365) ÷ 2*25
= ( 190.0338 ± √36112.84 - 20523.65) ÷ 50
= ( 190.0338 ± 124.85) ÷ 50 = 1.303 or 6.297 (approx.)
therefore, maximum point of bending will be gained at x = 6.297
(ii) A formula for the height of suspension bridge across the river Lune main cables has been
calculated as
Y = 0.00455x2 – 0.2275x +10
Calculate the lowest point of the suspension cable in distance (x) and height (y). Also calculate
the length of the suspension wires to the main road deck which is at 5.120m
Solution: The lowest point of suspension cable can be calculated by -
Y = 0.00455x2 – 0.2275x +10
differentiating both sides with respect to x,
dY/dx = d/dx (0.00455x2 – 0.2275x +10)
= 0.0091x – 0.2275
at maximum or minimum point, dY/dx = 0
which implies that, 0.0091x – 0.2275 = 0

x = 0.2275 / .0091
= 25
so, lowest point of suspension level in distance x = 25m and y = 0.00455 (25)2 – 0.2275 (25) +10
= 2.84 – 5.68 + 10
= 7.16m
Length of the suspension wires to the main road deck which is at 5.120m will be,
Y = 0.00455(5.120)2 – 0.2275 (5.120) +10
= 0.119 – 1.164 + 10
= 8.955m
(iii) Find the locations when the gradient of the voltage curve v given by the expression v =3(sin
4θ) equals zero
Solution: Expression of voltage v is given by,
v = 3 (sin 4θ)
differentiating the equation with respect to θ,
dv/dθ = d/dθ [3 (sin 4θ)]
v' = 3 cos 4θ . 4
= 12 cos 4θ
The locations can be calculated by taking first derivative at 0,
dv/dθ = 0
12 cos 4θ = 0
cos 4θ = 0
4θ = 0° or π
θ = 0° and π/4 or 45°

Task 2
(i) Calculate using calculus the location of the centre of gravity along the x axis for the profile of
the flood defence wall detailed on sheet 2.
Solutions: Total area of following figure = area of triangle + area of big rectangle + area of small
Rectangle
= ½ x 3.2 x 7 + 3.8 x 7 + 3.6 x 3.3
= 11.2 + 25.6 + 11.88
= 48.68 square unit.
Now, centre of gravity can be determined by,
Centre of gravity for triangle = h/3
= 7/3 = 2.33
Centre of gravity for rectangle = h/2
= 7/2 = 3.5
Centre of gravity for small rectangle = h/2
= 3.3/2 = 1.65
Therefore, total centre of gravity = 2.3 x 11.2 + 3.5 x 25.6 + 1.65 x 11.88
11.2 + 25.6 + 11.88
= 135.962 / 48.68
= 2.796
Therefore, centre of gravity of given figure is at a distance of 2.8 units from left corner of figure.

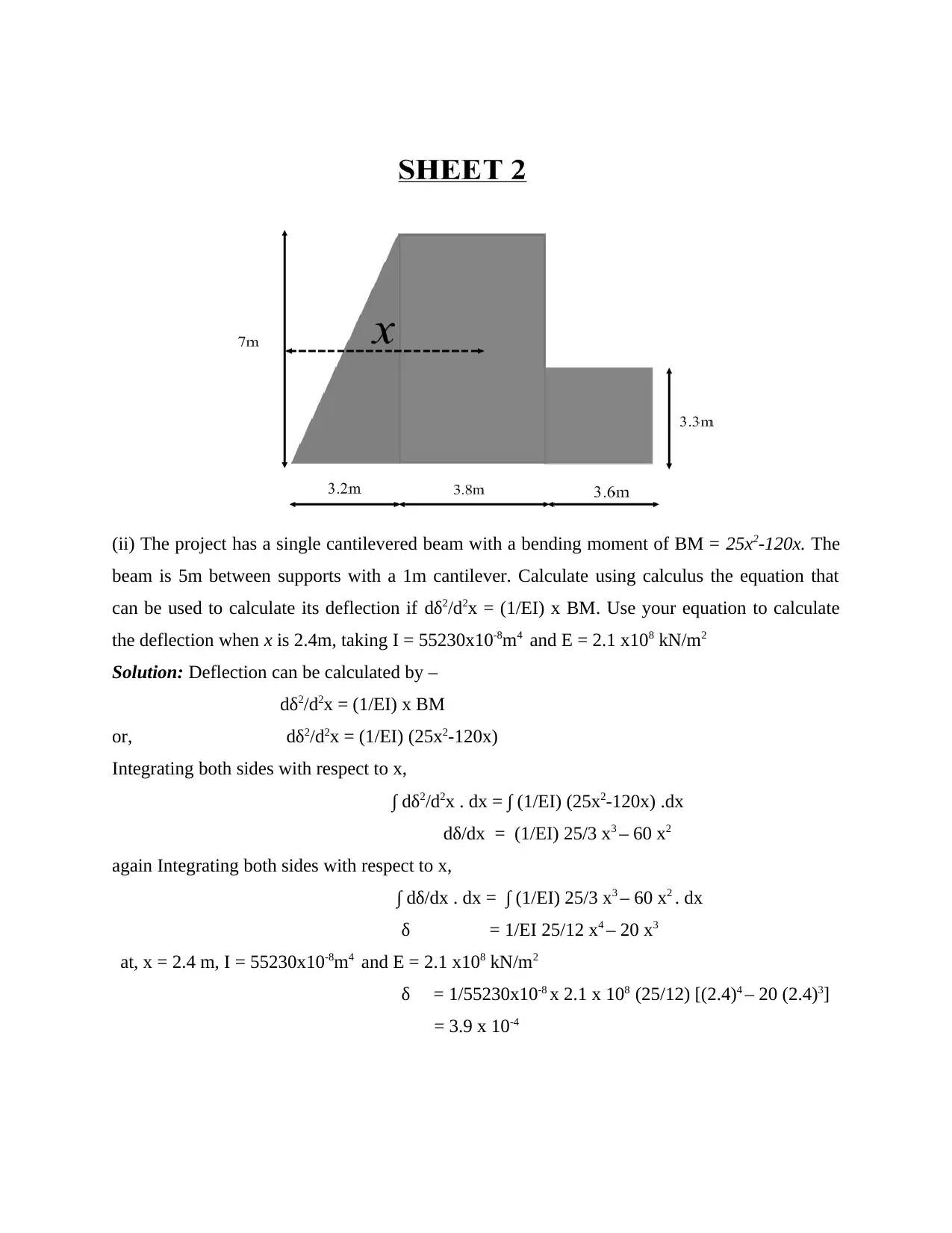
(ii) The project has a single cantilevered beam with a bending moment of BM = 25x2-120x. The
beam is 5m between supports with a 1m cantilever. Calculate using calculus the equation that
can be used to calculate its deflection if dδ2/d2x = (1/EI) x BM. Use your equation to calculate
the deflection when x is 2.4m, taking I = 55230x10-8m4 and E = 2.1 x108 kN/m2
Solution: Deflection can be calculated by –
dδ2/d2x = (1/EI) x BM
or, dδ2/d2x = (1/EI) (25x2-120x)
Integrating both sides with respect to x,
∫ dδ2/d2x . dx = ∫ (1/EI) (25x2-120x) .dx
dδ/dx = (1/EI) 25/3 x3 – 60 x2
again Integrating both sides with respect to x,
∫ dδ/dx . dx = ∫ (1/EI) 25/3 x3 – 60 x2 . dx
δ = 1/EI 25/12 x4 – 20 x3
at, x = 2.4 m, I = 55230x10-8m4 and E = 2.1 x108 kN/m2
δ = 1/55230x10-8 x 2.1 x 108 (25/12) [(2.4)4 – 20 (2.4)3]
= 3.9 x 10-4

TASK 3
(i) For a material, Newton’s law of cooling can be represented by the decay equation where t is
the time in seconds. And is the temperature at any given instant in time.
Calculate the initial temperature and the temperature that the body approaches as time
increases to infinity. Determine the rate of at t = 2.2 and 3.4 seconds by differentiation and give
your comment as you compare the results.
Solutions: Newton’s law of cooling can be represented by the given formula -
T(t) = Ts + ( T0 - Ts) e-kt
Here, T(t) denotes the temperature of object at time t,
Ts is temperature around surrounding and
T0 is initial temperature and k is decay constant
In this regard, when time goes to infinity then T(t) = T0
Therefore, differentiating both sides with respect to t, it is got -
d T(t) / dt = d/dt [ Ts + ( T0 - Ts) e-kt ]
T'(t) = -kt ( T0 - Ts) e-kt
In this regard, when time tends to infinity i.e. at t = ∞, then second term will tend to zero
or, T approaches to Ts, or T(t) = Ts and
so, initial time will be,
T(t) = Ts + ( T0 - Ts) e-kt
Put value of T(t) = Ts
Then, T0 = 0
so, k will be 1.
The rate of change of temperature is proportional to difference between initial temperature and
temperature at surrounding,
∫ dy = -k. ∫ (T- T0).dt
∫ 1/(T- T0) = ∫ -k. dt
ln | T- T0 | = -kt
| T- T0 | = e-kt
or, | T- T0 | = e-kt

at t = 2.2 and k = 1, | T- T0 | = e-2.2 = 0.11
at t = 3.4 and k = 1, | T- T0 | = e-3.4 = 0.33
Therefore, it has been calculated from above analysis that when at 3.4 sec, the rate of change of
temperature will be thrice that of temperature at 2.4 sec.

TASK 4
(i) A scaled model is to be produced for the new road layout on a nearby housing estate and the
centre line of the road has been expressed as an equation detailed below. Calculate the maxima
and minima points for the curve including checks and relevant analysis.
Y = -10x3 + 100x2 – 50x + 24
Solution: Given equation :
Y = -10x3 + 100x2 – 50x + 24
Taking differentiation on both sides with respect to x -
dY/dx = d/dx (-10x3 + 100x2 – 50x + 24)
Y' = -30x2 + 200x – 50 where, Y' = dY/dx
again differentiate both sides with respect to x,
dY'/dx = d/dx (-30x2 + 200x – 50)
Y'' = -60x + 200 where, Y'' = dY'/dx
taking differentiate again on both sides with respect to x,
dY''/dx = d/dx (-60x + 200)
Y''' = -60 < 0
Now, to find critical value -
put Y' = 0
-30x2 + 200x – 50 = 0
on solving, we get x = +(10 - √85) / 3
x = (0 , 6)
For maxima and minima,
at x = 0
Y' (0) = -50 <0
Therefore, at x = 0, function will attains its maximum value which will be 24.

(ii) To calculate maximum volume at 1197 width mm and 793 breadth mm.
Solution: Let Planter box will be in cylindrical shape then, h = 1197 mm and c = 793 mm (c is
circumference of base of box)
then, volume of cylindrical box = Area x height
= π r2 x h
Where, r is radius of circle will be calculated as,
2 π r = 793
2 x 3.14 x r = 793
or, r = 793 / 6.28
r = 126.273
therefore, volume of box will be – V = π r2 x h
= 3.14 x (126.273)2 x 1197
= 59671216.08 mm
(iii) Find the maximum and minimum values of the voltage v given by the expression
v = 3 (sin 4θ) between , and including values of θ =0 and θ =2π radians
Solution: Given Voltage,
v = 3 (sin 4θ)
differentiating the equation with respect to θ,
dv/dθ = d/dθ [3 (sin 4θ)]
v' = 3 cos 4θ . 4
= 12 cos 4θ
at θ = 0 v' = 12 cos 4(0)
= 12 .1
= 12 < 0 therefore, at θ = 0, the function will get its minimum value.
at θ = 2π, v' = 12 cos 4(2π)
= 12 .1
= 12 < 0 therefore, at θ = 0, the function will get its minimum value.

(iv) An existing road has the following average flow rates measured over an 8 hour period. The
data has been collected for the last 5 years...
Year Average daily rates of vehicles over
a 8 hour day
2014 1500
2015 1577
2016 1658
2017 1743
2018 1832
a) Determine the relative growth rate
Solution: Relative Growth rate = (Present / Past)1/n - 1 here, present = 1832 and
past = 1500, n = 5
= (1832 / 1500)1/5 – 1
= (1.22)1/5 - 1
= 1.04 – 1
= 0.04 = 4%.
b) Write a general equation for the population
Solution: Population = Present Population (1 + Growth Rate)Time
y = a (1 + r%)T
= 1832 (1 + 4%)T
= 1832 (1.04)T
c) Estimate the vehicles number by 2025
Solution: at t = 7 years, number of vehicles will be,
y = 1832 (1.04)T
= 1832 (1.04)7
= 1832 x 1.315
= 2410 (approx)
d) How many years will it take for the vehicles to double in daily flow rate from the 2014 figure?
Solution: In 2014, number of vehicles was 1500, so it will be double in the year-
t = ?, y = 1500 (1.04)T
3000 = 1500 (1.04)T
(1.04)T = 2

T = 18 years
i.e. in context with 2014, in the year 2032 the number of vehicles will be doubled.