Calculus 1 Homework Assignment: Analyzing Functions and Optimization

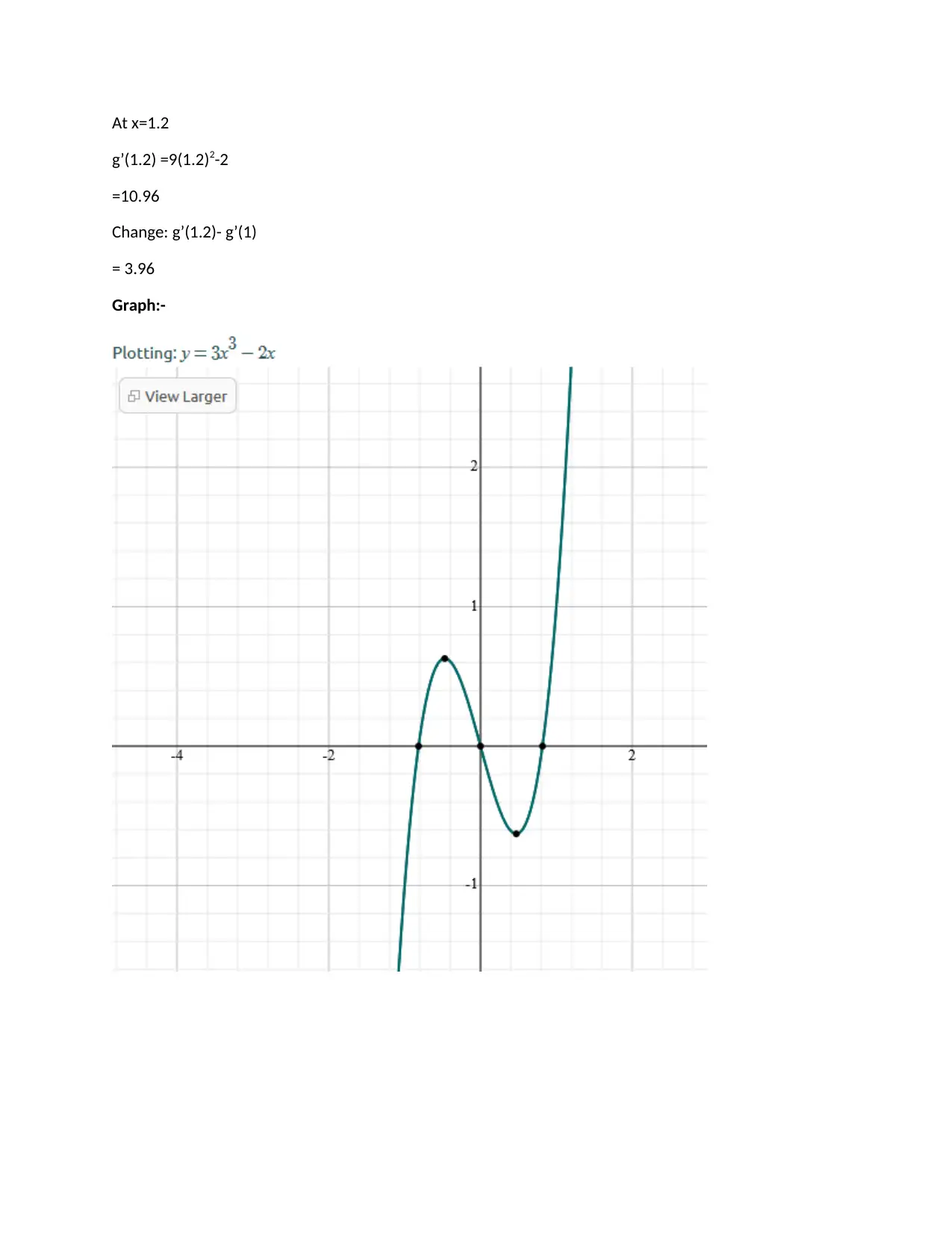
This Calculus 1 assignment solution provides a comprehensive analysis of several calculus problems. The solution begins by examining the increasing and decreasing intervals of a function, determining critical points and local extrema, and identifying the points of inflection. It then delves into optimization problems, finding the dimensions that minimize the cost function and the area of a fenced region. Furthermore, the solution covers the concepts of rates of change and the application of derivatives in these scenarios. The document also includes the analysis of asymptotes and graphing of functions. Each problem is approached systematically, with detailed calculations and explanations to facilitate understanding. The assignment covers a wide range of topics typically encountered in a first-semester calculus course, including function analysis, derivatives, optimization, and graphing. This solution is a valuable resource for students seeking to understand and master these concepts.

Math algebra and calculus

1 Solution:- f(x) = 2x3+x2-20x+1
1(a) Solution:-Condition for increasing or decreasing function
Case:-1 if f’(x) <0 for x then f is decreasing
Case:-2 if f’(x) >0 for x then f is increasing
Case:-3 if f’(x) =0 for x then f is constant
f(x) = 2x3+x2-20x+1
f’(x) = 6x2+2x-20
f’(x) =2(3x2+x-10)
f’(x) =2(3x2+6x-5x-10)
f’(x) =2(3x(x+2) -5 (x+2))
Therefore
X=5/2 and x=-2
Put these value of x in the equation
f(5/3) =2(5/3)3+(5/3)2-20(5/3)+1
f(5/3) = 9.2 +2.77-33.3+1
=-20.3: decreasing
Put f(-2)
f(x) = 2(-2)3+(-2)2-20(-2)+1
=-16+4+41
= 29 : increasing
1.b Solution:-
f(x) = 2x3+x2-20x+1
f’(x) = 6x2+2x-20
f’’(x) = 12x+2
= 2(6x+1)

X=-1/6
LHS f ‘’(X)<0 RHS f’’(X)>0
Graph:-
Test in f ‘’(X)
Point of Inflection at x=-1/6

f’’(x) = 12x+2
Ist:-x=-1/5
f’’(-1/5) = 12(-1/5)+2
f’’(-1/5) =-2/5<0------- CD
2nd :- x=0
f’’(x) = 12x+2
f’’(0) = 12(0)+2
f’’(0) = 2>0……………..CU
Therefore CD<-1/6 and CU x>-1/6
Interval (-1/6, 1/6)
POI (Point Of Inflection):
At x= -1/6
f(x) = 2x3+x2-20x+1
f(-1/6) = 2(-1/6)3+(-1/6)2-20(-1/6)+1
f(-1/6) = -0.0046 +0.0277-3.33+1
f(-1/6) = -2.3489
At x= 1/6
f(x) = 2x3+x2-20x+1
f(1/6) = 2(1/6)3+(1/6)2-20(1/6)+1
f(1/6) = 3.4033
1.c Solution:-
POI (Point Of Inflection) =-1/6
Local extreme maxima at (-2,29)
Local extreme maxima at (5/3, -548/27)
Y intercept (0,1)
Graph:-

)
2. Solution:-
2.1(a):-
C= 40x2+1225
Rate = Cx
Rate = (40x2+1225)x
Rate = 40 x3+1225 x
Differentiate R =f (x)
dR = (dR/dx)*dx
dR/dx= (40 x3+1225 x)dx
dR/dx= (120x2+1225)
x varies 10 to 12 unnits
dR = (120(10)2+1225)………………………..(1)
cost $13255

2.1(b):-
The value of Δ R= f(x+ Δ x)-f(x)
Rate = (40x2+1225)
Δ R = R(12)- R(10)
Δ R = 6985-5225
Δ R= $ 1760
3. Solution:-
f(x) = x3-12x+20
3.1 Solution:-:-
f’(x) = 3x2-12x
f’(x) = 3x(x-12)
x=0
x=12
X -infinity 0 12 +infinity
f’(x) +ve +ve +ve +ve
f(x) increasing increasing increasing increasing
This is a monotonic function.
f’(-1)= 3+ 12 = 15 : +ve
f’(0)=20
3.2 Solution:-
f(x) = x3-12x+20
f’(x) = 3x2-12x
f’’(x) = 6x-12
6x=12
x=2

Consider interval ( --infinity, 2) and (2, +infinity)
Interval (--infinity, 2) (2, +infinity)
Sign f’(x) - +
f(x) Concave Down Concave UP
f’(-1) = 3(-1)2-12(-1) <0 :CD
f’(3) = 3(3)2-12(-1) >0 :CU
3.3 Solution:-
Critical Point at x=-2 and x=2
Put x=-2 into f(x) = x3-12x+20
Y= 36
Maximum (-2, 36)
Put x=2 into f(x) = x3-12x+20
Y=4
Minimum (2, 4)
Therefore: Maximum (-2, 36)
Minimum (2, 4)
Point of inflection =2
Graph:-

4 Solutions:-
4.1 (a) Solution:-Let the length of fencing =y
Width =x
Area=xy=92
Perimeter of three sides
P=2x+y
= 2x+92/x
dp/dx=2-92/x2
dp/dx=0
= 2-92/x2
2=92/x2
x2=46
x= √46
put the value of x in xy =92
√46 y=92

Y=92/√46
Y=92/6.7
Y=13.73
4.2 Solution:-
= 2-92/x2
4.2 Solution:-
On differentiating again it becomes
dp/dx=2-92/x2
d2p/ dx2=2-92/x2
d2p/ dx2= 92/x3
when x>7
d2p/ dx2>0 Minimum
5 Solutions:-
5.1 Solution:-Asymptotes of f(x)= (4x-2)/(2x-6)
On simplify (4x-2)/(2x-6)
(2x-1)/(x-3)
Vertical Asymptotes is known as zeroes of denominator
It becomes (2x-1)/(x-3)
Vertical Asymptotes is x=3 (Singularity Points)
Horizontal Asymptotes is y=2
Vertical: x=3
Horizontal : y=2
5.2 Solution:- Graph

6 Solution:-
g(x) = 3x3-2x
On differentiating
g’(x) =9x2-2
at x=1
g’(1) =9(1)2-2
=7

At x=1.2
g’(1.2) =9(1.2)2-2
=10.96
Change: g’(1.2)- g’(1)
= 3.96
Graph:-