Calculus and Vectors: Solving Derivatives, and Area Problems

This document presents a comprehensive solution to a mathematics assignment, focusing on key concepts in calculus and vector analysis. The assignment includes detailed solutions to problems involving vector operations such as addition, scalar multiplication, and finding parallel vectors. It also covers derivative calculations for various functions, including polynomial, trigonometric, and logarithmic functions, applying chain rule and power rule. The assignment further explores finding critical points, determining minima and maxima, and calculating the area of a parallelogram using vector cross products. Additionally, it includes optimization problems, such as finding the dimensions of a soft drink cartoon that minimize surface area while maintaining a specific volume. References to relevant books and journals are provided to support the solutions.

MATHEMATICS
ADVANCE

Question 1
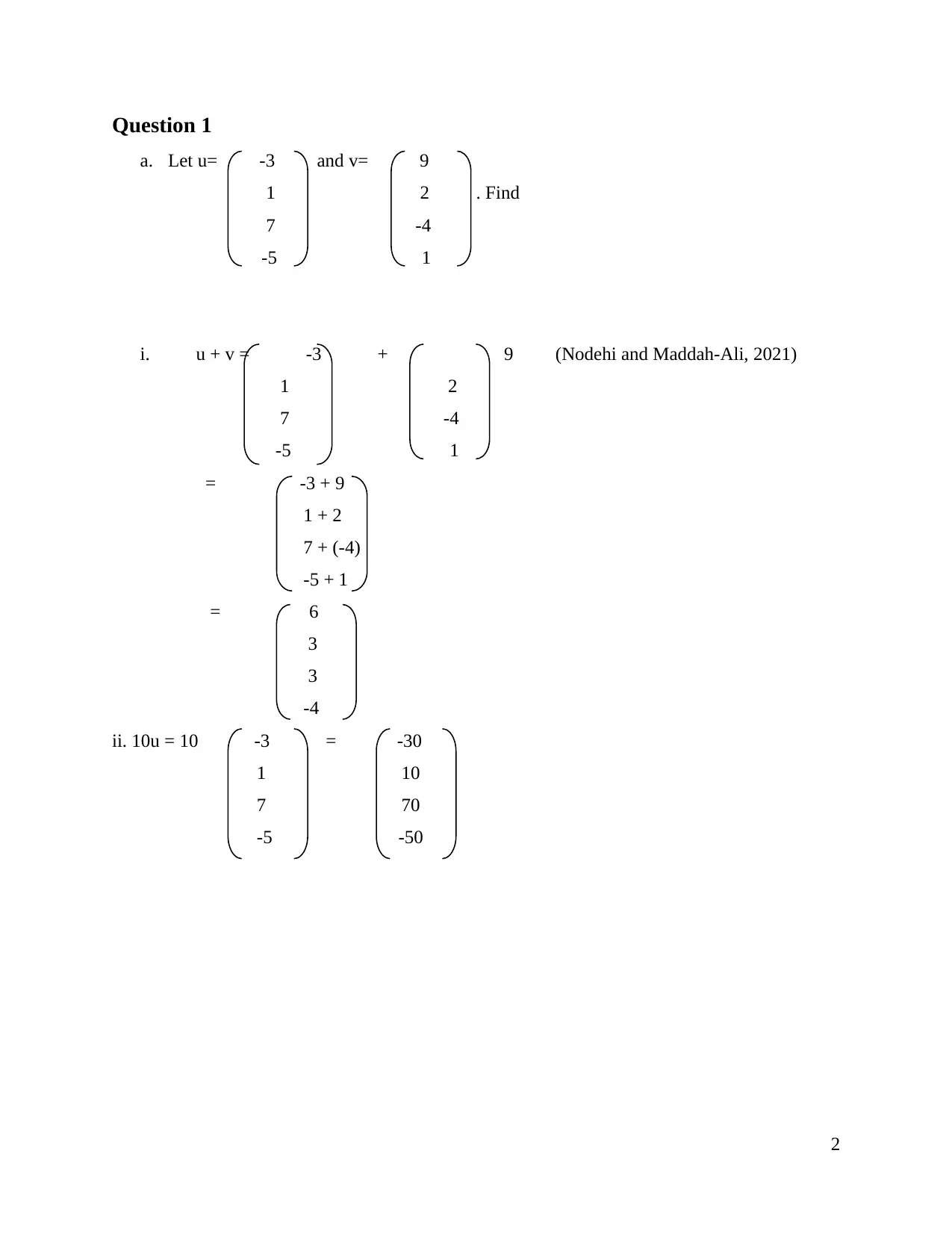
a. Let u= -3 and v= 9
1 2 . Find
7 -4
-5 1
i. u + v = -3 + 9 (Nodehi and Maddah-Ali, 2021)
1 2
7 -4
-5 1
= -3 + 9
1 + 2
7 + (-4)
-5 + 1
= 6
3
3
-4
ii. 10u = 10 -3 = -30
1 10
7 70
-5 -50
2

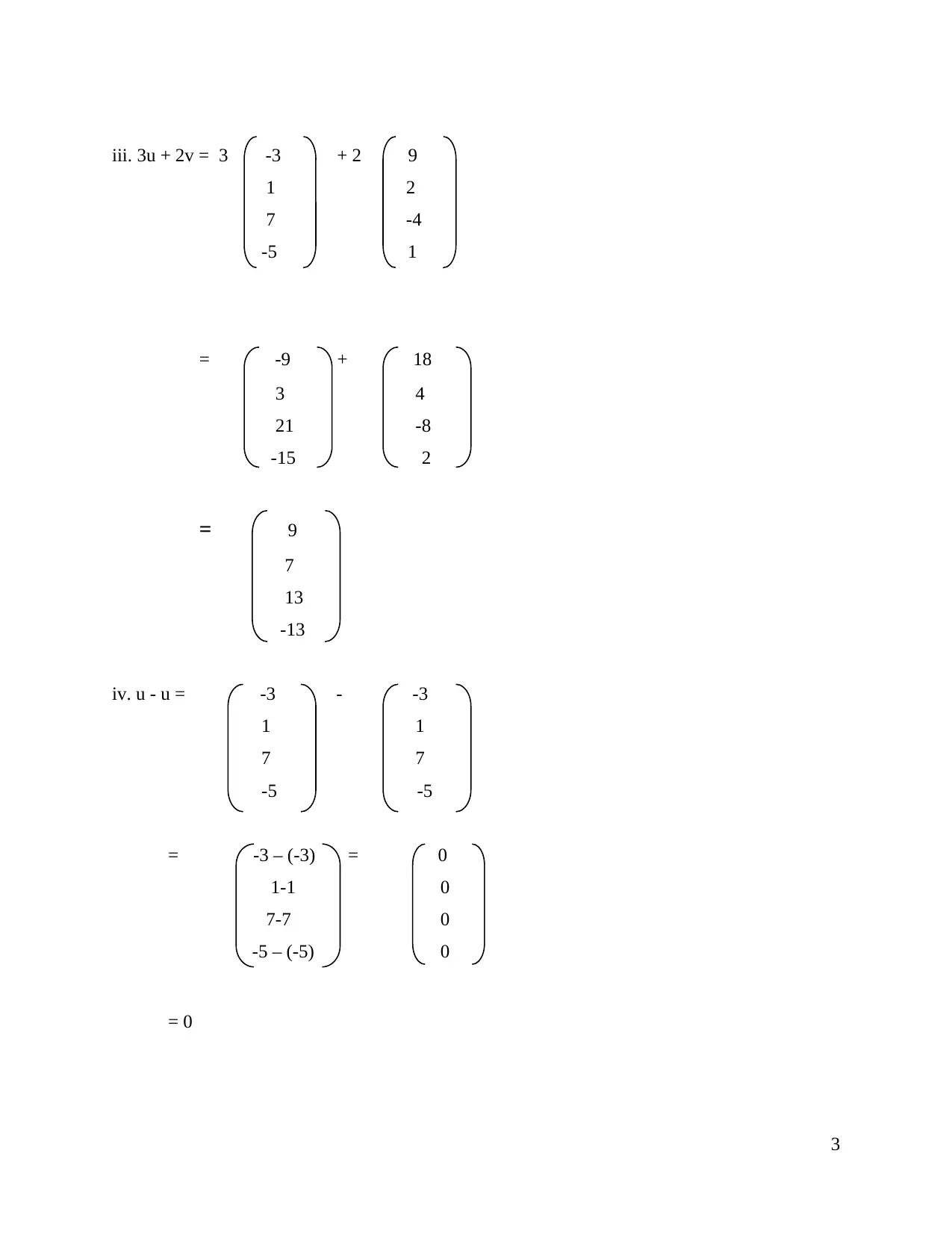
iii. 3u + 2v = 3 -3 + 2 9
1 2
7 -4
-5 1
= -9 + 18
3 4
21 -8
-15 2
= 9
7
13
-13
iv. u - u = -3 - -3
1 1
7 7
-5 -5
= -3 – (-3) = 0
1-1 0
7-7 0
-5 – (-5) 0
= 0
3

v. -2u – 8v = -2 -3 - 8 9
1 2
7 -4
-5 1
= 6 - 72
-2 16
-14 -32
10 8
= -66
-18
18
2
b. Given that 2 and 8 are parallel vectors,
-3 y
Find the value of y.
Solution: Since the given two vectors are parallel, let
8 = k 2 = 2k where k is a scalar (Jia, Qian and Yuan, 2017).
y -3 -3k
2k = 8
k=4
y= -3k = -3 (4) = -12
Question 2
4

a. The column vectors p and q are defined by
p = 8 – x , q = x – 4
6 – y y + 2
Given that p = q
i. Find the value of x and y.
Solution: Since, the column vectors p and q are equal, then (Boukaram, Turkiyyah and
Keyes, 2019)
8-x = x-4 and 6-y = y+2
x+x = 8+4 and y+y = 6-2
2x = 12 and 2y = 4
x = 6 and y = 2.
ii. p = 8-6 and q= 6-4
6-2 2+2
p = 2 and q = 2
4 4
|p| = √22+42 = √20 = 2√5 ; |q| =2√5
b. Find the area of the parallelogram with edges v = 2i+j-3k and w = i+3j+2k.
Solution. Area of parallelogram = |u * v| (Bagóczki and Bánhelyi, 2017)
i j k
2 1 -3
1 3 2
= i {2*1- (3*-3)} – j {2*2- (-3*1)} + k {2*3-1*1}
= i {2-(-9)} – j{4- (-3)} + k {6-1}
= i (11) – j (7) + k (5)
= 11i – 7j + 5k
5

|v*w| = √112 + 72 + 52
= √121+49+25
= √195
c. Show that vector p = 6i + 9j is parallel to q = 4i+6j.
Solution. In order to show that two vectors are same,
λp = q (Rote, 2019)
λ 6 = 4
9 6
6 λ = 4 ; λ = 4/6 = 2/3
9 λ = 6 ; λ = 6/9 = 2/3
Since, the value of both λ are same, the vectors are parallel.
Question 3
a. Find the derivatives of the following functions:
i. y = (x2 – 7x)(x - 1)
Solution: This is of the form y = uv
So, u = (x2 – 7x) and v = (x - 1)
By implementing the formula,
u (dv/dx) + v (dy/dx)
= (x2 – 7x) d/dx (x-1) + (x-1) d/dx (x2 – 7x)
= (x2 – 7x)(1-0) + (x-1) (2x-7)
= x2 – 7x + 2x2 -7x – 2x + 7
= 3x2 – 14x – 2x +7
= 3x2 -16x + 7
ii. y = Sin (2x)
Let f(x) = sin x and g(x) = 2x
Then, it is found that h(x) = fog (x) = sin2x
According to the chain rule of differentiation,
Since, it is known that d/dx (sin x) = cos x
6

So, d/d(2x) {sin (2x)} = cos2x
Also, d/dx (2x) = 2
Furthermore, by using chain rule of differentiation (Freund and Rathjen, 2021),
d/dx sin2x = d/d(2x) sin (2x) d/dx (2x)
= cos2x (2) = 2 cos 2x
iii. y = x2 – 10x + 3, and determine its minimum value.
By using the power rule,
d/dx [xn] = nxn-1
d/dx (x2 – 10x + 3) = 2x – 10
To find the minima, we need to find the critical points which are found by putting
the derivative equals to 0 (Quezada, 2020).
2x-10 = 0
x = 10/2
x = 5
Putting the value of x = 5 in the equation x2 – 10x + 3, we get
52-10*5+3 = 25-50+3 = -22
(5, -22) is a local minima.
iv. y = ln (3t - 5)7/2t+1
y = ln (3t - 5) 7 – ln (2t+1)
= 7 ln (3t - 5) – ln (2t + 1)
dy/dx = {7/3t – 5} (3) – {1/2t+1} (2)
= {21/3t-5} – {2/2t+1}
b. Find dy/dx if x2+y2 = 2xy
x2+y2 = 2xy
2x + 2ydy/dx = 2xy + 2xdy/dx
2x-2xy = (2x-2y)dy/dx
dy/dx = 2x-2xy/2x-2y
dy/dx = 2x (1-y)/2x-2y
7

Question 4
a. Find the critical points for f (x) = x3/3-x2/2-6x+100
f’(x) = x2-x-6
Then, the roots are to be found. The roots are also known as the zeros and are the x
values where the graph basically intersects the x-axis (Tarasov and Tarasova, 2020).
Putting the equation equal to 0, the roots which are the critical points are found as:
x = 3, -2.
b. i. Surface area of soft drink cartoon = A
Since, surface area of Cuboid = 2 (lw+wh+hl)
l = 2x, w = x, h = h
A = 2 (2x*x+x*h+2xh)
A = 4x2+2xh+4xh
A = 4x2+6xh
Since, capacity = 1000 cm3 = l*b*h
2x*x*h=1000
2x2*h=1000
h=1000/2x2
Putting the value of h in the value of A, we get
A= 4x2+6x (1000/2x2)
A= 4x2+3000/x
ii. If A is stationary, this means dA/dx=0
dA/dx= 8x-3000/x2 = 0
8x=3000/x2
x3=3000/8
x= (3000/8)1/3
x=5(3)1/3
x=7.21124785...
iii. For finding minimum value of A,
8

dA/dx=0
8x-3000/x2 = 0
x=5(3)1/3 and 300(9)1/3
The local minima of A is (5(3)1/3, 300(9)1/3)
9

REFERENCES
Books and Journals
Bagóczki, Z. and Bánhelyi, B., 2017. A parallel interval arithmetic-based reliable computing
method on a GPU. Acta Cybernetica. 23(2). pp.491-501.
Boukaram, W., Turkiyyah, G. and Keyes, D., 2019. Hierarchical matrix operations on GPUs:
Matrix-vector multiplication and compression. ACM Transactions on Mathematical
Software (TOMS). 45(1). pp.1-28.
Freund, A. and Rathjen, M., 2021. Derivatives of normal functions in reverse
mathematics. Annals of Pure and Applied Logic. 172(2). p.102890.
Jia, S., Qian, X. and Yuan, X., 2017. Optimal design for dividing wall column using support
vector machine and particle swarm optimization. Chemical Engineering Research and
Design. 125. pp.422-432.
Nodehi, H.A. and Maddah-Ali, M.A., 2021. Secure coded multi-party computation for massive
matrix operations. IEEE Transactions on Information Theory.
Quezada, V.D., 2020. Difficulties and performance in mathematics competences: solving
problems with derivatives. International Journal of Engineering Pedagogy
(iJEP). 10(4). pp.35-53.
Rote, G., 2019. The Largest Contained Quadrilateral and the Smallest Enclosing Parallelogram
of a Convex Polygon. arXiv preprint arXiv:1905.11203.
Tarasov, V.E. and Tarasova, S.S., 2020. Fractional derivatives and integrals: What are they
needed for?. Mathematics. 8(2). p.164.
10