Calculus Assignment: Solving Differential Equations and Analysis

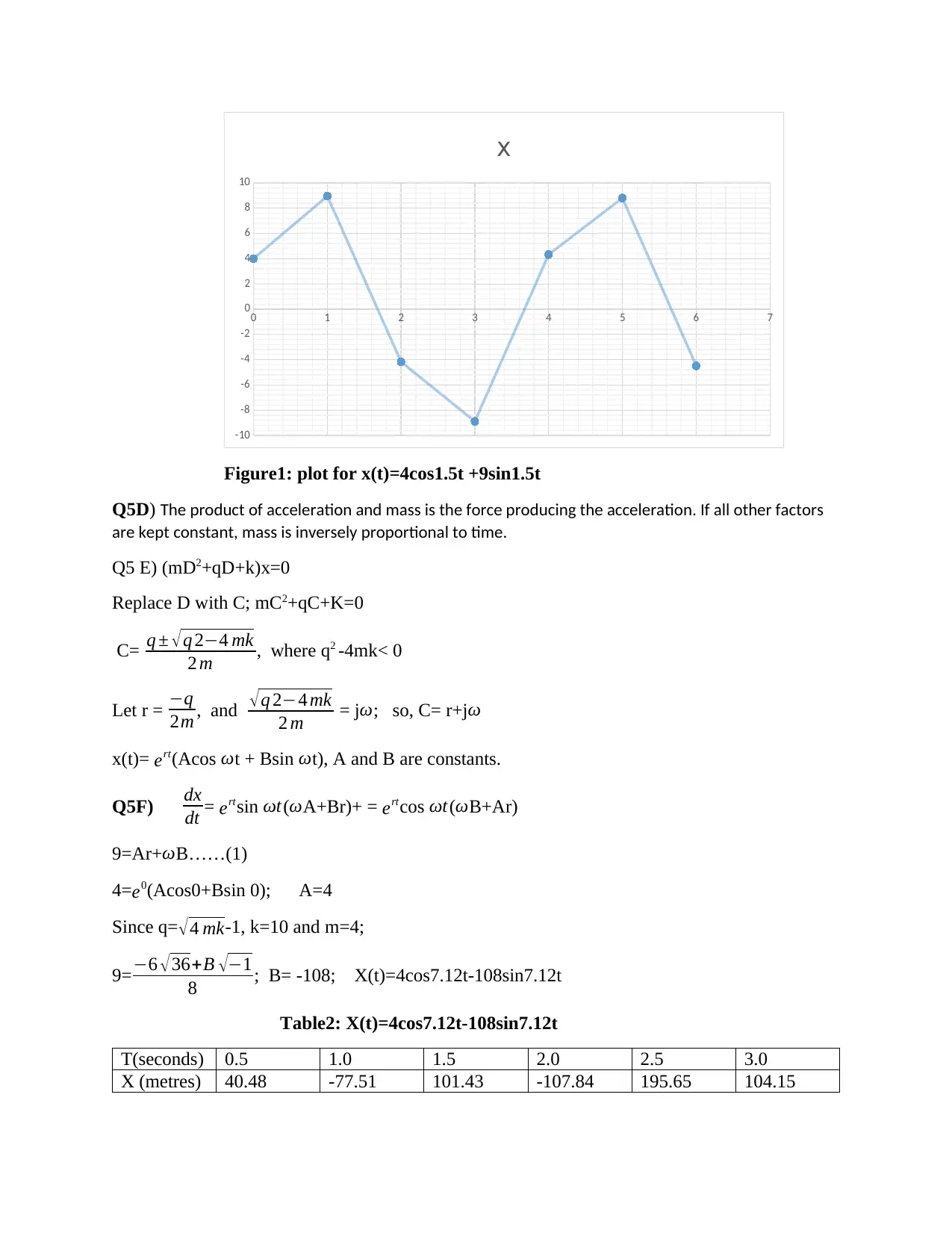
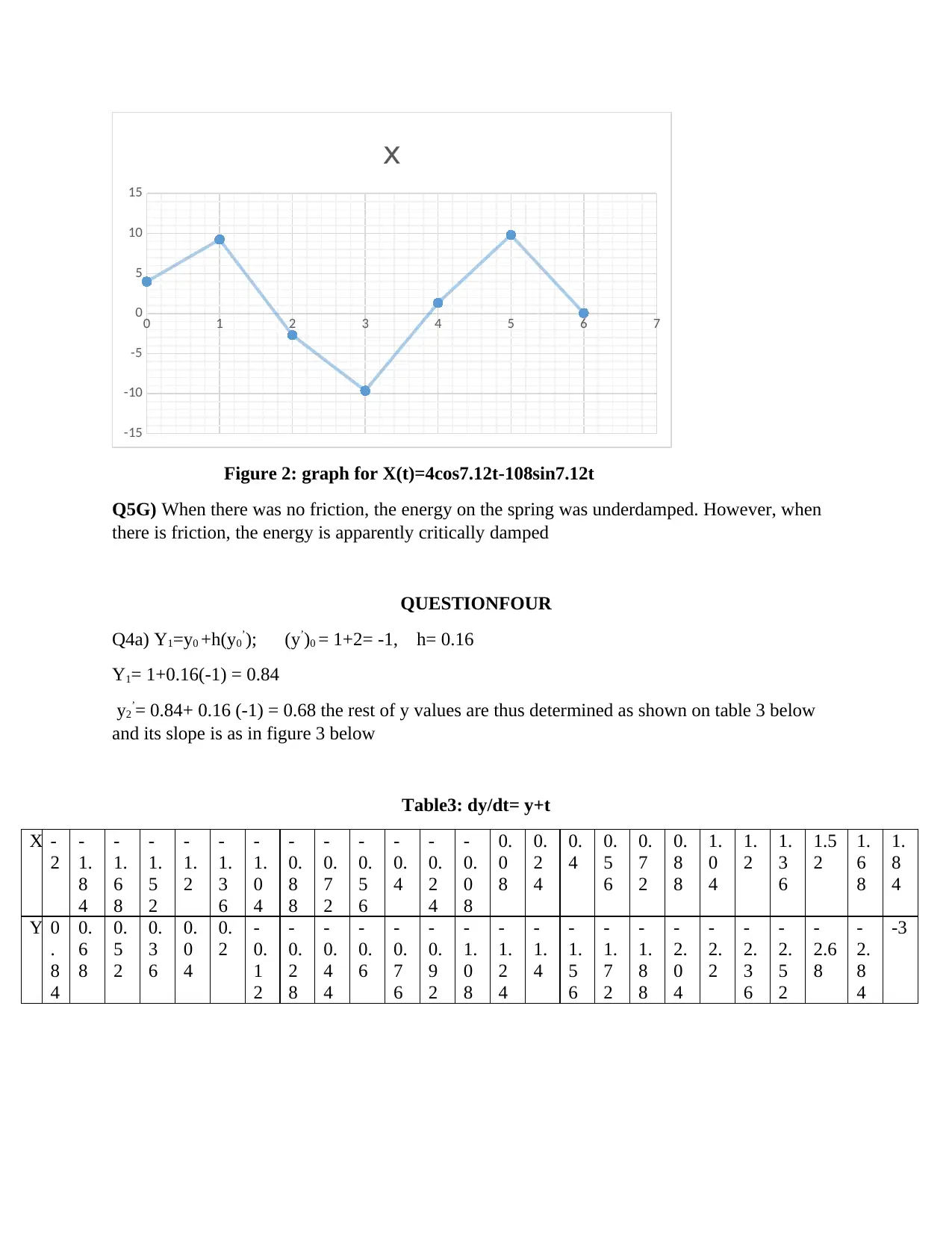
This assignment presents solutions to problems in calculus, specifically focusing on differential equations and numerical methods. The solution begins by solving second-order differential equations with constant coefficients, exploring cases with complex roots and oscillatory solutions. It then applies these concepts to a spring-mass system, analyzing both underdamped and critically damped scenarios. The assignment also includes an application of Euler's method for approximating solutions to differential equations. Furthermore, it addresses initial conditions and the relationship between mass, acceleration, and force. The assignment provides tables and graphs to visualize the solutions and the behavior of the systems under different conditions. It also demonstrates the application of calculus in solving physical problems. The assignment covers topics from calculus and differential equations to provide a comprehensive analysis of different systems.

QUESTION 5
Q5A) substitute D operator for dy
dx ,: (aD2+bD+C)x=0
Substituting m for D: am2+ bm+C=0
m= −b ± √ b2−4 ac
2a but r = -b/2a and ω= √4 ac−b2
2 a hence, jω = √b2−4 ac
2 a ,since b2 ≠ 4ac
hence, m= r±jω, ( complex roots). Therefore x(t) = ert(C1cos ωt+ C2sin ωt).
Q5B) (aD2+K)x=0
Substituting C for D: mC2+K=0; C= ± √−k
m , Let C= ±jω (since the C is complex)
Therefore, x(t)= e0(Acos ωt + Bsin ωt); Hence x(t) = Acos ωt + Bsin ωt
Q5C) x(t) = 0Acos ωt + Bsin ωt
Assume the initial conditions: y(0) =4, dx
dt = 9,
At x(0) =4, 4=Acos 0 + Bsin 0 i.e. A=4……….(i)
dx
dx = -ωAsinωt+ Bcos ωt; 9= 0 + Bcos 0; B=9…...(ii)
Hence x(t)= 4cos ωt + 9 sin ωt
Let m=N7+1=3+1=4, and k= N8+1=9+1=10,
Hence, (4D2+10)X= 0;
Replacing D with C; 4C2+10=0; C= ± √ −10
4 = ± j 1.58
X(t)= 4cos 1.58t +9sin 1.58t
Table 1: X(t)=4cos 1.58t + 9sin 1.58t
t in
seconds(s)
0 1.0 2.0 3.0 4.0 5.0 6.0
X in
metres
(m)
4 8.96 -4.17 -8.89 4.33 8.81 -4.49

0 1 2 3 4 5 6 7
-10
-8
-6
-4
-2
0
2
4
6
8
10
x
Figure1: plot for x(t)=4cos1.5t +9sin1.5t
Q5D) The product of acceleration and mass is the force producing the acceleration. If all other factors
are kept constant, mass is inversely proportional to time.
Q5 E) (mD2+qD+k)x=0
Replace D with C; mC2+qC+K=0
C= q ± √q 2−4 mk
2 m , where q2 -4mk< 0
Let r = −q
2m , and √q 2−4 mk
2 m = jω; so, C= r+j ω
x(t)= ert(Acos ωt + Bsin ωt), A and B are constants.
Q5F) dx
dt = ertsin ωt (ωA+Br)+ = ertcos ωt(ωB+Ar)
9=Ar+ωB……(1)
4= e0(Acos0+Bsin 0); A=4
Since q= √4 mk-1, k=10 and m=4;
9=−6 √36+B √−1
8 ; B= -108; X(t)=4cos7.12t-108sin7.12t
Table2: X(t)=4cos7.12t-108sin7.12t
T(seconds) 0.5 1.0 1.5 2.0 2.5 3.0
X (metres) 40.48 -77.51 101.43 -107.84 195.65 104.15

0 1 2 3 4 5 6 7
-15
-10
-5
0
5
10
15
x
Figure 2: graph for X(t)=4cos7.12t-108sin7.12t
Q5G) When there was no friction, the energy on the spring was underdamped. However, when
there is friction, the energy is apparently critically damped
QUESTIONFOUR
Q4a) Y1=y0 +h(y0’); (y’)0 = 1+2= -1, h= 0.16
Y1= 1+0.16(-1) = 0.84
y2’= 0.84+ 0.16 (-1) = 0.68 the rest of y values are thus determined as shown on table 3 below
and its slope is as in figure 3 below
Table3: dy/dt= y+t
X -
2
-
1.
8
4
-
1.
6
8
-
1.
5
2
-
1.
2
-
1.
3
6
-
1.
0
4
-
0.
8
8
-
0.
7
2
-
0.
5
6
-
0.
4
-
0.
2
4
-
0.
0
8
0.
0
8
0.
2
4
0.
4
0.
5
6
0.
7
2
0.
8
8
1.
0
4
1.
2
1.
3
6
1.5
2
1.
6
8
1.
8
4
Y 0
.
8
4
0.
6
8
0.
5
2
0.
3
6
0.
0
4
0.
2
-
0.
1
2
-
0.
2
8
-
0.
4
4
-
0.
6
-
0.
7
6
-
0.
9
2
-
1.
0
8
-
1.
2
4
-
1.
4
-
1.
5
6
-
1.
7
2
-
1.
8
8
-
2.
0
4
-
2.
2
-
2.
3
6
-
2.
5
2
-
2.6
8
-
2.
8
4
-3

-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
Y
Figure3: slope of dy/dt= y+t
Q4B) y(0.2) =-1.4
Q4C) y0’=1+0= 1, y0.1=1+(1⨯0.1)= 1.1.
y1’=1.1+0.2= 1.32; y0.2= 1.1+0.1(1.32) = 1.232
Q4D) mt,y(t))=f(0+0.1/2, i+0.1/2 (1)); m= (0.5,1.05)
Y(0+0.1)= 1+1.05
Y(0+0.1)= 2.05
Y(0.1+0.1)= 2.05+1= 3.0