Calculus Homework: Differentiation, Exponential, Logarithm Functions

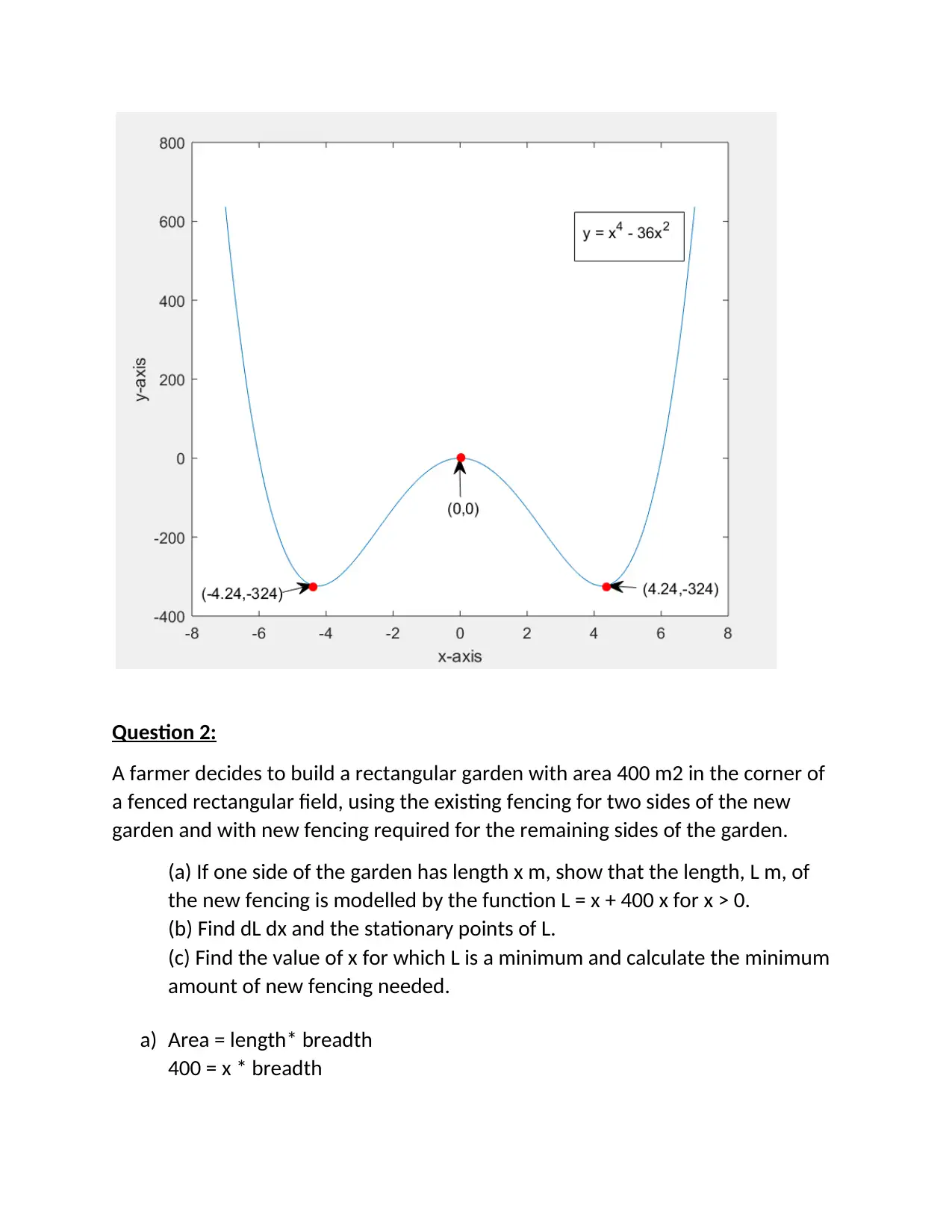
This document presents a comprehensive set of solutions to calculus assignments, encompassing a range of topics from differentiation and its applications to exponential and logarithmic functions, and also includes integration problems. The assignments cover finding derivatives using first principles, sketching graphs, solving equations, determining turning points, and applying these concepts to real-world scenarios such as population growth and optimization problems. The solutions demonstrate step-by-step workings and explanations, providing a valuable resource for students studying calculus. The assignment also includes problems on complex numbers and their applications. The problems range in difficulty and cover a wide array of calculus concepts. The document is a useful resource for students seeking to understand and solve complex calculus problems.

Assignment 6 :
Question 3:
f) 2 x
√x2 +7 ¿ ¿ = d
dx ( 2 x
√ x2+7 ¿ ¿)
= 2. d
dx ( x
√ x2+7 ¿ ¿)
=2.
d
dx ( x ) . √ x2 +7−x . d
dx ( √ x2 +7 )
( √ x2 +7 )
2
=2. 1 √ x2+7− 1
2 ( ( x2 +7 )
1
2−1
) . d
dx ( x2+7 ) . x
x2+7
=¿)
= 2 ( √ x2 +7− x2
√ x2 +7 )
x2 +7
= 2
√ x2 +7 − 2 x2
( x2+ 7 )
3
2 (Answer)
Assignment 7:
Question 1:

Question 2:
A farmer decides to build a rectangular garden with area 400 m2 in the corner of
a fenced rectangular field, using the existing fencing for two sides of the new
garden and with new fencing required for the remaining sides of the garden.
(a) If one side of the garden has length x m, show that the length, L m, of
the new fencing is modelled by the function L = x + 400 x for x > 0.
(b) Find dL dx and the stationary points of L.
(c) Find the value of x for which L is a minimum and calculate the minimum
amount of new fencing needed.
a) Area = length* breadth
400 = x * breadth

Breadth = 400
x
breadth = 400/x
length = x
Garden
Since two adjacent sides of garden are covered with old fence, the length
new fence required is
L = Length +Breadth
L = x + 400
x
b) L = x + 400
x
dL
dx = 1 - 400
x 2
For stationary points dL
dx =0
1 - 400
x 2 = 0
X2 = 400
X = 20m
At x =20m,
L = 20 + 400/20
= 20 +20
= 40m
(x, L) = (20, 40)

c) Minima of L is at stationary point dL
dx =0,
1 - 400
x 2 = 0
X2 = 400
X = 20m
At x =20m,
L = 20 + 400/20
= 20 +20
= 40m
(x, L) = (20, 40)
L = 40 is the minimum value of L.
Therefore, minimum amount of new fencing needed is 20m.
-------------------------------------------------------------------------------------------------------------
Assignment-8
Question 3:
A. Simplifying
e^4x -4e^2x = 0
Reorder the terms:
-4e^2x + e^4x = 0
Solving
-4e^2x + e^4x = 0
Solving for variable 'e'.

Factor out the Greatest Common Factor (GCF), 'e2x'.
e^2x(-4 + e^2x) = 0
Factor a difference between two squares.
e^2x((2 + e^x)(-2 + e^x)) = 0
case1:
e^2x = 0
x = 0
case2:
2 + e^x = 0
e^x = -2
since value of e^x is never negative, this case is discarded.
Case3:
-2 + e^x = 0
e^x = 2
ln(e^x) = ln(2) …..{Taking antilog on both sides}
x = ln(2)
x = 0.6931
therefore, considering all three cases, the value of x is 0 and 0.6391.
x = {0, 0.6391}
Question 4:
Y = ex +e− x
turning points determined by dy
dx =0
dy
dx = ex - e− x

ex- e− x = 0
e2 x= 1
x = 0
Y = ex +e− x
Y = e0+e0 = 1 +1 = 2
turning point = (x, y) = (0,2)
This point is global minima of the equation.
-x <---------------------------------------|------------------------------------+x
(-) (0) (+)
Question 6:
A. The initial population is at time t = 0.
Therefore, put t=0 in equation,
P(t) = 10000
1+ 1000 = 10(approx. value)
B. The carrying capacity of population is the maximum capacity of population.
At t= ∞, population will be maximum because denominator(1+1000e^(-
0.2t)) is minimum.
at t = ∞, e^(-0.2t) = 0
hence, 1000(e^(-0.2t)) = 0
Putting the above values in P(t) equation gives us,
P(t) = 10000
1+o = 10000
C. P(t) = 5000 …..{Given}
5000 = 10000
1+ 1000 e−0.2t

1 + 1000 e−0.2 t = 10000
5000
1 + 1000 e−0.2 t = 2
1000 e−0.2 t = 2-1 =1
e−0.2 t = 0.001
e0.2 t = 1000
ln(e0.2 t) = ln(1000)
0.2t = ln(1000)
T= 5*ln(1000) = 34.5388 years.
D. P(t) = 9000 …..{Given}
9000 = 10000
1+ 1000 e−0.2 t
1 + 1000 e−0.2 t = 10000
9000
1000 e−0.2 t = 10
9 -1
1000 e−0.2 t = 1
9
e−0.2 t = 1
9000
e0.2t= 9000
ln (e0.2 t )= ln(9000) …..{Taking log on both sides}
0.2t = ln(9000)
t=5(ln9000)
t =45.5249 years
population will be 9000 after 45.5249 years