Calculus Assignment: Solving Problems in Differentiation & Integration
VerifiedAdded on 2023/06/12
|7
|2556
|306
Homework Assignment
AI Summary
This calculus assignment provides detailed solutions to a range of problems covering differentiation and integration techniques. It includes finding derivatives of various functions using rules like the quotient rule, product rule, and chain rule. The assignment also addresses applications of calculus, such as finding turning points of curves, determining maximum and minimum values, and solving optimization problems. Additionally, it covers integration, including indefinite and definite integrals, with examples involving trigonometric functions and partial fractions. The problems are solved step-by-step, offering a comprehensive guide for students studying calculus. Desklib offers a wealth of similar solved assignments and past papers to aid students in their studies.

CALCULUS
Author
Department
Institution
City, Country
Address
Question 1
a.
7 x2+ 2
x3 +5 3
√ x−1
dy
dx ()=7 d
dx ( x2 )+2 d
dx (x ¿¿−3)+5 d
dx (x
1
3 )−0 ¿
¿ 7 ( 2 ) ( x2−1 ) +2(−3)( x¿¿−3−1)+5 ( 1
3 ) x
1
3 −1
¿
¿ 14 x−6 x− 4+ 5
3 x
−2
3
b. y=In ( 3 x−2 )
Let 3 x−2=u , so that y=lnu
dy
du = 1
u , du
dx =3
dy
dx = dy
du × du
dx = 1
u × 3= 3
u = 3
3 x−2
c. y=5 sin 3 x
dy
dx = d
dx ¿
Let 3 x=u , so that y=sinu
dy
du =cosu , du
dx =3
dy
dx =5 dy
du × du
dx =5 ( cosu ) (3 )=15 cosu=15 cos (3 x)
d.
y= 3 e2 x
x3
We apply the quotient rule to obtain
dy
dx =
x3 d
dx ( 3 e2 x ) −3 e2 x d
dx (x3 )
(x3 )2
¿ x3 (6 e¿¿ 2 x)−3 e2 x(3 x2)
x6 ¿
¿ 6 x3 e2 x−9 x2 e2 x
x6 = 6 x e2 x−9 e2 x
x4
e. y=x3 cos 4 x
We apply the product rule to obtain
dy
dx =x3 d
dx ( cos 4 x )+ cos 4 x d
dx ( x ¿¿ 3)¿
¿ x3 ( −4 sin 4 x ) + cos 4 x (3 x ¿¿ 2) ¿
¿−4 x3 sin (4 x )+3 x2 cos (4 x )
¿ 3 x2 cos ( 4 x)−4 x3 sin ( 4 x)
f.
y= ( x2−7 ) 6
Let x2−7=u , so that du
dx =2 x ,∧ y=u6
dy
du = d
du (u¿¿ 6)=6u5 ¿
dy
dx = dy
du × du
dx =6u5 × 2 x=12 x u5=12 x ( x2−7)5
Question 2
Part a
y=x3 e2 x
at x = 2
We apply the product rule as follows
dy
dx =x3 d
dx (e2 x )+e2 x d
dx ( x3 )
¿ x3 ( 2 e2 x ) +e2 x ( 3 x2 )
dy
dx =2 x3 e2 x+3 x2 e2 x
Author
Department
Institution
City, Country
Address
Question 1
a.
7 x2+ 2
x3 +5 3
√ x−1
dy
dx ()=7 d
dx ( x2 )+2 d
dx (x ¿¿−3)+5 d
dx (x
1
3 )−0 ¿
¿ 7 ( 2 ) ( x2−1 ) +2(−3)( x¿¿−3−1)+5 ( 1
3 ) x
1
3 −1
¿
¿ 14 x−6 x− 4+ 5
3 x
−2
3
b. y=In ( 3 x−2 )
Let 3 x−2=u , so that y=lnu
dy
du = 1
u , du
dx =3
dy
dx = dy
du × du
dx = 1
u × 3= 3
u = 3
3 x−2
c. y=5 sin 3 x
dy
dx = d
dx ¿
Let 3 x=u , so that y=sinu
dy
du =cosu , du
dx =3
dy
dx =5 dy
du × du
dx =5 ( cosu ) (3 )=15 cosu=15 cos (3 x)
d.
y= 3 e2 x
x3
We apply the quotient rule to obtain
dy
dx =
x3 d
dx ( 3 e2 x ) −3 e2 x d
dx (x3 )
(x3 )2
¿ x3 (6 e¿¿ 2 x)−3 e2 x(3 x2)
x6 ¿
¿ 6 x3 e2 x−9 x2 e2 x
x6 = 6 x e2 x−9 e2 x
x4
e. y=x3 cos 4 x
We apply the product rule to obtain
dy
dx =x3 d
dx ( cos 4 x )+ cos 4 x d
dx ( x ¿¿ 3)¿
¿ x3 ( −4 sin 4 x ) + cos 4 x (3 x ¿¿ 2) ¿
¿−4 x3 sin (4 x )+3 x2 cos (4 x )
¿ 3 x2 cos ( 4 x)−4 x3 sin ( 4 x)
f.
y= ( x2−7 ) 6
Let x2−7=u , so that du
dx =2 x ,∧ y=u6
dy
du = d
du (u¿¿ 6)=6u5 ¿
dy
dx = dy
du × du
dx =6u5 × 2 x=12 x u5=12 x ( x2−7)5
Question 2
Part a
y=x3 e2 x
at x = 2
We apply the product rule as follows
dy
dx =x3 d
dx (e2 x )+e2 x d
dx ( x3 )
¿ x3 ( 2 e2 x ) +e2 x ( 3 x2 )
dy
dx =2 x3 e2 x+3 x2 e2 x
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

When x=2
dy
dx =2(2)3 e2(2)+3 ( 2 )2 e2 (2 )=16 e4 +12 e4=e4 ( 16+12 )=28 e4=1528.75
Part b
y=sin 3 x
x2 at x= π
4
We apply the quotient rule to obtain
dy
dx =
x2 d
dx ( sin ( 3 x ) ) −sin ( 3 x ) d
dx (x2)
(x2)2
¿ x2 ( 3 cos ( 3 x ) )−sin ( 3 x ) (2 x )
x4
¿ 3 x cos ( 3 x ) −2 sin(3 x)
x3
When x= π
4
dy
dx =
3 π
4 cos (3 π
4 )−2sin ( 3 π
4 )
( π
4 )
3
¿
3 π
4 ( − √ 2
2 ) −2 ( √ 2
2 )
π
64
3 =
−64 ( 3 π √ 2
8 − √ 2)
π3
¿ −8 √ 2 ( 3 π +8 )
π3 =−6.358
Question 3
y=2 x3−9 x2+ 12 x +1
To get the turning points, we determine the derivative of the
curve and then equate it to zero as follows:
dy
dx =0= d
dx ( 2 x3−9 x2 +12 x +1 )
d
dx ( 2 x3 −9 x2+12 x+ 1 )=6 x2−18 x+ 12=0
a=6 , b=−18 , c=12
x= 18 ± √ (−18)2 −4 (6 ×12)
2× 6 =18 ± √ 324−288
12 = 18 ± 6
12 = 24
12
x= 24
12 =2∨x=12
12 =1
x=1∨x =2
when x=1 , y=2(1)3−9 ( 1 )2+ 12 ( 1 ) +1=6
when x=2 , y=2(2)3−9 ( 2 ) 2 +12 ( 2 ) +1=5
Hence, the turning points are ( 1 , 6 )∧(2 ,5)
To determine whether the points are maximum, we choose
values on either sides of the turning points and evaluate the
derivatives as summarized in table 1 below.
dy
dx =6 x2−18 x+12
When x=0 x=1when x=1.5 x=2 when x=3
dy
dx
12( positive)0 −1.5( negative)0 12( positive)
Sig
n ¿ −¿ ¿ −¿ ¿
Therefore, we can see that ( 1 , 6 )is a maximum point whereas
(2 , 5) is a minimum point.
Question 4
x=2 t3−15 t2+24 t +4
Part a
The velocity , v= dx
dt = d
dt (2 t3 −15 t2 +24 t +4)
¿ 6 t2−30 t+24
When t=5 , v =6(5)2−30 ( 5 ) +24=24 m/ s
Part b
dy
dx =2(2)3 e2(2)+3 ( 2 )2 e2 (2 )=16 e4 +12 e4=e4 ( 16+12 )=28 e4=1528.75
Part b
y=sin 3 x
x2 at x= π
4
We apply the quotient rule to obtain
dy
dx =
x2 d
dx ( sin ( 3 x ) ) −sin ( 3 x ) d
dx (x2)
(x2)2
¿ x2 ( 3 cos ( 3 x ) )−sin ( 3 x ) (2 x )
x4
¿ 3 x cos ( 3 x ) −2 sin(3 x)
x3
When x= π
4
dy
dx =
3 π
4 cos (3 π
4 )−2sin ( 3 π
4 )
( π
4 )
3
¿
3 π
4 ( − √ 2
2 ) −2 ( √ 2
2 )
π
64
3 =
−64 ( 3 π √ 2
8 − √ 2)
π3
¿ −8 √ 2 ( 3 π +8 )
π3 =−6.358
Question 3
y=2 x3−9 x2+ 12 x +1
To get the turning points, we determine the derivative of the
curve and then equate it to zero as follows:
dy
dx =0= d
dx ( 2 x3−9 x2 +12 x +1 )
d
dx ( 2 x3 −9 x2+12 x+ 1 )=6 x2−18 x+ 12=0
a=6 , b=−18 , c=12
x= 18 ± √ (−18)2 −4 (6 ×12)
2× 6 =18 ± √ 324−288
12 = 18 ± 6
12 = 24
12
x= 24
12 =2∨x=12
12 =1
x=1∨x =2
when x=1 , y=2(1)3−9 ( 1 )2+ 12 ( 1 ) +1=6
when x=2 , y=2(2)3−9 ( 2 ) 2 +12 ( 2 ) +1=5
Hence, the turning points are ( 1 , 6 )∧(2 ,5)
To determine whether the points are maximum, we choose
values on either sides of the turning points and evaluate the
derivatives as summarized in table 1 below.
dy
dx =6 x2−18 x+12
When x=0 x=1when x=1.5 x=2 when x=3
dy
dx
12( positive)0 −1.5( negative)0 12( positive)
Sig
n ¿ −¿ ¿ −¿ ¿
Therefore, we can see that ( 1 , 6 )is a maximum point whereas
(2 , 5) is a minimum point.
Question 4
x=2 t3−15 t2+24 t +4
Part a
The velocity , v= dx
dt = d
dt (2 t3 −15 t2 +24 t +4)
¿ 6 t2−30 t+24
When t=5 , v =6(5)2−30 ( 5 ) +24=24 m/ s
Part b

acceleration= dv
dt = d
dt ( 6 t2−30 t +24)
¿ 12 t −30
When t=1 , acceleration=12 ( 1 ) −30=−18 m/s2
Part c
At rest , velocity=0. That is,
6 t2−30 t+24=0 , a=6 , b=−30 , c=24
t= 30 ± √(−30)2−4 (6 ×24)
2 ×12 = 30 ± √900−576
24 = 30 ±18
24 = 48
24 ∨12
24
∴ t=2 sec∨t=0.5 sec
Part d
From part b, acceleration=12t −30
When acceleration=6 m/s2 we can get the time as follows
12 t−30=6
12 t=6+30=36
12t
12 =36
12 =3 ,t=3 sec
Question 5
E=1.16−(5.232× 10−3 )T −(7 ×10−6) T2
To get the maximum E, we equate the derivative of the
function to zero as follows
dE
dt =0=0−5.232× 10−3−2 ¿
2 ¿
T =−5.232× 10−3
2 ¿¿
Maximum
E=1.16−(5.232× 10−3 )(−373.7143)−(7× 10−6 )(−373.7143)2
Emax=1.16+1.95527−0.97764=2.13763
Question 8
volume of cylinder=π r2 h=1000, h=1000
π r2
S . A of cylinder=2 π r 2+2 πrh=2 π r 2+2 πr ( 1000
π r2 )
S . A=2 π r 2+ 2000
r
To minimize area, d ( S . A )=0. That is,
d
dr ( 2 π r2 + 2000
r )=0
4 πr −2000
r2 =0
( 4 πr− 2000
r2 ) r2=0 (r2)
4 π r3 −2000=0
4 π r3 =2000
r3 =2000
4 π = 500
π
radius=3
√ 500
π =5.42 cm
We get the corresponding height as
h=1000
π r2 =h= 1000
π (5.42)2 =10.84 cm
Question 9
a. ∫5 e2 x + 3
√ x4 dx
∫5 e2 x + 3
√ x4
dx=5∫e2 x dx +∫ x
4
3 dx
¿ 5 ( 1
2 e
2 x
)+ x
4
3 +1
4
3 +1
+C
¿ 5
2 e2 x + x
7
3
7
3
+C
dt = d
dt ( 6 t2−30 t +24)
¿ 12 t −30
When t=1 , acceleration=12 ( 1 ) −30=−18 m/s2
Part c
At rest , velocity=0. That is,
6 t2−30 t+24=0 , a=6 , b=−30 , c=24
t= 30 ± √(−30)2−4 (6 ×24)
2 ×12 = 30 ± √900−576
24 = 30 ±18
24 = 48
24 ∨12
24
∴ t=2 sec∨t=0.5 sec
Part d
From part b, acceleration=12t −30
When acceleration=6 m/s2 we can get the time as follows
12 t−30=6
12 t=6+30=36
12t
12 =36
12 =3 ,t=3 sec
Question 5
E=1.16−(5.232× 10−3 )T −(7 ×10−6) T2
To get the maximum E, we equate the derivative of the
function to zero as follows
dE
dt =0=0−5.232× 10−3−2 ¿
2 ¿
T =−5.232× 10−3
2 ¿¿
Maximum
E=1.16−(5.232× 10−3 )(−373.7143)−(7× 10−6 )(−373.7143)2
Emax=1.16+1.95527−0.97764=2.13763
Question 8
volume of cylinder=π r2 h=1000, h=1000
π r2
S . A of cylinder=2 π r 2+2 πrh=2 π r 2+2 πr ( 1000
π r2 )
S . A=2 π r 2+ 2000
r
To minimize area, d ( S . A )=0. That is,
d
dr ( 2 π r2 + 2000
r )=0
4 πr −2000
r2 =0
( 4 πr− 2000
r2 ) r2=0 (r2)
4 π r3 −2000=0
4 π r3 =2000
r3 =2000
4 π = 500
π
radius=3
√ 500
π =5.42 cm
We get the corresponding height as
h=1000
π r2 =h= 1000
π (5.42)2 =10.84 cm
Question 9
a. ∫5 e2 x + 3
√ x4 dx
∫5 e2 x + 3
√ x4
dx=5∫e2 x dx +∫ x
4
3 dx
¿ 5 ( 1
2 e
2 x
)+ x
4
3 +1
4
3 +1
+C
¿ 5
2 e2 x + x
7
3
7
3
+C
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

¿ 5
2 e2 x + 3
7 x
7
3 + C
b. ∫ 3
4 x dx
∫ 3
4 x dx= 3
4 ∫ 1
x dx= 3
4 ln ( x )+C
c. ∫ 4 √ x dx
∫ 4 √ x dx=4∫ x
1
2 dx=4 × x
1
2 +1
1
2 +1
+C
¿ 4 × x
3
2
3
2
+C=8
3 x
3
2 +C
d. ∫
0
π
cos x+sin 2 x dx
∫
0
π
cos x+sin 2 x dx=∫
0
π
cos xdx +∫
0
π
sin 2 x dx
¿|sin ( x)|0
π
+|−1
2 cos ( 2 x)|0
π
¿ ( 0−0 )− 1
2 ( cos ( 2 π ) −cos ( 0 ) )
¿−1
2 ( 1−1 )=0
e. ∫2 x ln x dx
∫2 x ln x dx=2∫ x ln x dx
We apply the Chain rule :∫udv=uv−∫ vdu as follows
We let x=u so that du=dx, and let
lnx=dv so that v =∫lnxdx=1/ x
uv−∫ vdu=x ( 1
x )−∫ ( 1
x )dx
¿ 1−ln ( x ) +C
Question 10
a. ∫
0
1
( 5 x−6 ) 5 dx
Let 5 x−6=u , dx= 1
5 du
∫
0
1
( 5 x−6 )5 dx =∫
0
1
1
5 u
5
du
∫ 1
5 u
5
= 1
5 ( 1
6 u
6
)= 1
30 u
6
= 1
30 (5 x−6)6
∫
0
1
( 5 x−6 )5 dx =| 1
30 ( 5 x−6 )6
|0
1
¿ 1
30 ((5(1)−6)¿¿ 6−( 5(0)−6)6 ) ¿
¿ 1
30 ((−1)¿¿ 6−(−6)6 )¿
¿ 1
30 ( 1−46656 )=−1555.167
b. ∫
0
π
4
x sinx dx
We apply the Chain rule :∫udv=uv−∫ vdu as follows
We let x=u so that du=dx, and let
sinx=dv so that v=∫ sinxdx=−cosx
uv−∫ vdu=x ( −cosx ) −∫ ( −cosx ) dx
¿−xcosx+sinx
uv−∫ vdu=sinx−xcosx
∫
0
π
4
x sinx dx=|sinx−xcosx|0
π
4
¿ ¿
¿ 1
√2 (1− π
4 )=0.15175
c. ∫
0
1
12−4 x
x2+2 x−3 dx
First, we evaluate the function into partial fraction as follows
12−4 x
x2 +2 x−3 = 12−4 x
x2+3 x−x−3 = 12−4 x
x (+3)−1( x +3)= 12−4 x
( x−1)(x+ 3)
12−4 x
( x−1)(x +3)= A
(x−1) + B
(x +3)
2 e2 x + 3
7 x
7
3 + C
b. ∫ 3
4 x dx
∫ 3
4 x dx= 3
4 ∫ 1
x dx= 3
4 ln ( x )+C
c. ∫ 4 √ x dx
∫ 4 √ x dx=4∫ x
1
2 dx=4 × x
1
2 +1
1
2 +1
+C
¿ 4 × x
3
2
3
2
+C=8
3 x
3
2 +C
d. ∫
0
π
cos x+sin 2 x dx
∫
0
π
cos x+sin 2 x dx=∫
0
π
cos xdx +∫
0
π
sin 2 x dx
¿|sin ( x)|0
π
+|−1
2 cos ( 2 x)|0
π
¿ ( 0−0 )− 1
2 ( cos ( 2 π ) −cos ( 0 ) )
¿−1
2 ( 1−1 )=0
e. ∫2 x ln x dx
∫2 x ln x dx=2∫ x ln x dx
We apply the Chain rule :∫udv=uv−∫ vdu as follows
We let x=u so that du=dx, and let
lnx=dv so that v =∫lnxdx=1/ x
uv−∫ vdu=x ( 1
x )−∫ ( 1
x )dx
¿ 1−ln ( x ) +C
Question 10
a. ∫
0
1
( 5 x−6 ) 5 dx
Let 5 x−6=u , dx= 1
5 du
∫
0
1
( 5 x−6 )5 dx =∫
0
1
1
5 u
5
du
∫ 1
5 u
5
= 1
5 ( 1
6 u
6
)= 1
30 u
6
= 1
30 (5 x−6)6
∫
0
1
( 5 x−6 )5 dx =| 1
30 ( 5 x−6 )6
|0
1
¿ 1
30 ((5(1)−6)¿¿ 6−( 5(0)−6)6 ) ¿
¿ 1
30 ((−1)¿¿ 6−(−6)6 )¿
¿ 1
30 ( 1−46656 )=−1555.167
b. ∫
0
π
4
x sinx dx
We apply the Chain rule :∫udv=uv−∫ vdu as follows
We let x=u so that du=dx, and let
sinx=dv so that v=∫ sinxdx=−cosx
uv−∫ vdu=x ( −cosx ) −∫ ( −cosx ) dx
¿−xcosx+sinx
uv−∫ vdu=sinx−xcosx
∫
0
π
4
x sinx dx=|sinx−xcosx|0
π
4
¿ ¿
¿ 1
√2 (1− π
4 )=0.15175
c. ∫
0
1
12−4 x
x2+2 x−3 dx
First, we evaluate the function into partial fraction as follows
12−4 x
x2 +2 x−3 = 12−4 x
x2+3 x−x−3 = 12−4 x
x (+3)−1( x +3)= 12−4 x
( x−1)(x+ 3)
12−4 x
( x−1)(x +3)= A
(x−1) + B
(x +3)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
12−4 x= A ( x +3 ) + B(x−1)
When x=1
12−4(1)= A ( 1+3 ) + B( 1−1)
8=4 A , A=2
When x=−3
12−4(−3)= A (−3+3 ) + B(−3−1)
24=−4 B , B=−6
∴ 12−4 x
(x−1)( x+3)= A
(x−1) + B
(x+3)= 2
( x−1)+ −6
( x+3)
Then we find the integral and evaluate the limits as follows
∫
0
1
12−4 x
x2+2 x−3 dx=∫
0
1
2
(x−1) dx +∫
0
1
−6
( x +3) dx
¿ 2∫
0
1
1
( x−1) dx−6∫
0
1
1
(x +3) dx
¿ 2 |ln ( x−1)|0
1
−6|ln (x +3)|0
1
¿ 2 { ln 0−ln ( −1 ) }−6 {ln 4−ln 3 }
¿ 2 {ln ( 0
−1 ) }−6 {ln ( 4
3 ) }
¿ ln ( 0 )=∞
Question 11
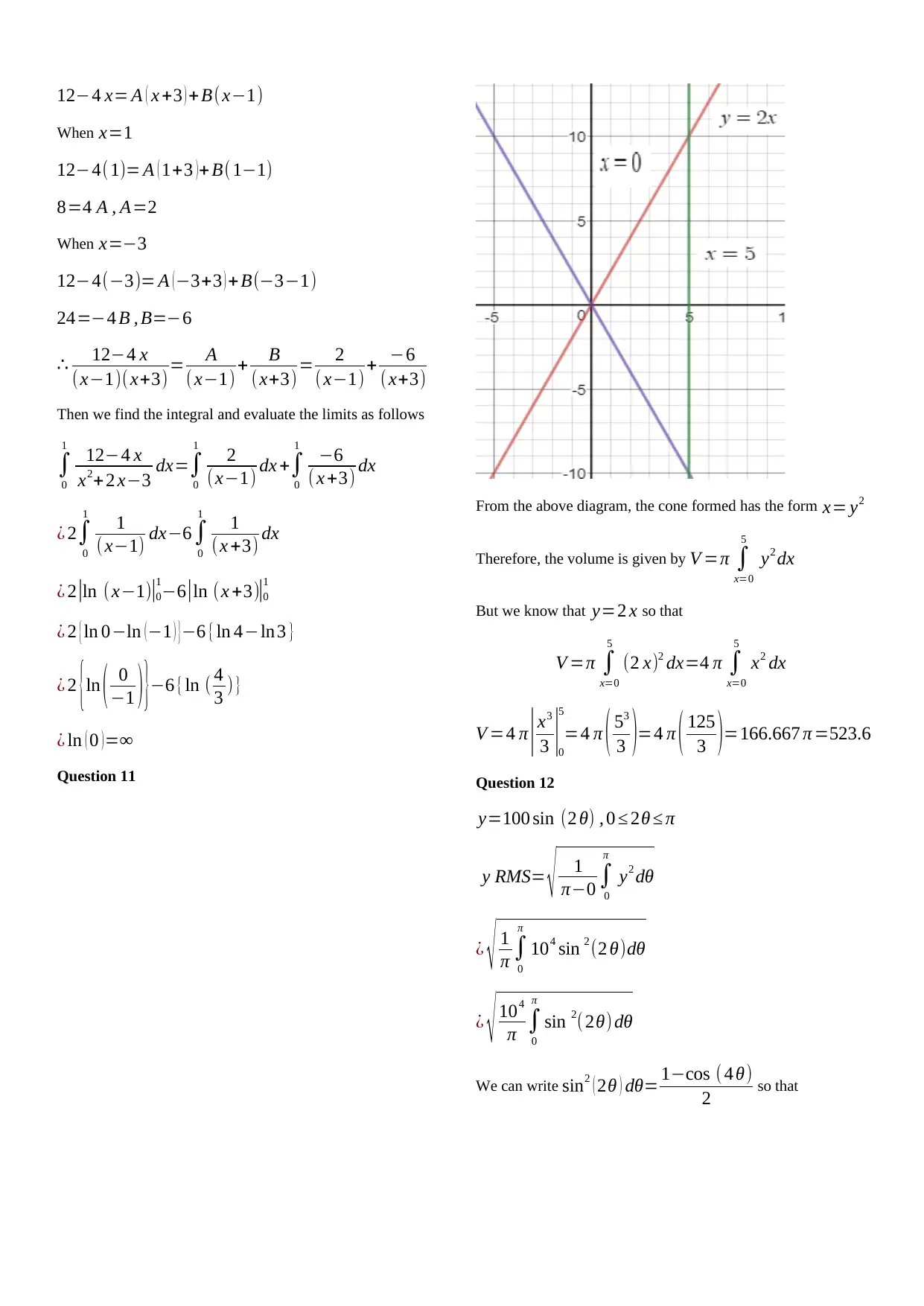
From the above diagram, the cone formed has the form x= y2
Therefore, the volume is given by V =π ∫
x=0
5
y2 dx
But we know that y=2 x so that
V =π ∫
x=0
5
(2 x)2 dx=4 π ∫
x=0
5
x2 dx
V =4 π |x3
3 |0
5
=4 π ( 53
3 )=4 π ( 125
3 )=166.667 π =523.6
Question 12
y=100 sin (2 θ) , 0 ≤ 2θ ≤ π
y RMS= √ 1
π−0 ∫
0
π
y2 dθ
¿ √ 1
π ∫
0
π
104 sin 2 (2 θ)dθ
¿ √ 104
π ∫
0
π
sin 2(2θ) dθ
We can write sin2 ( 2θ ) dθ= 1−cos ( 4 θ)
2 so that
When x=1
12−4(1)= A ( 1+3 ) + B( 1−1)
8=4 A , A=2
When x=−3
12−4(−3)= A (−3+3 ) + B(−3−1)
24=−4 B , B=−6
∴ 12−4 x
(x−1)( x+3)= A
(x−1) + B
(x+3)= 2
( x−1)+ −6
( x+3)
Then we find the integral and evaluate the limits as follows
∫
0
1
12−4 x
x2+2 x−3 dx=∫
0
1
2
(x−1) dx +∫
0
1
−6
( x +3) dx
¿ 2∫
0
1
1
( x−1) dx−6∫
0
1
1
(x +3) dx
¿ 2 |ln ( x−1)|0
1
−6|ln (x +3)|0
1
¿ 2 { ln 0−ln ( −1 ) }−6 {ln 4−ln 3 }
¿ 2 {ln ( 0
−1 ) }−6 {ln ( 4
3 ) }
¿ ln ( 0 )=∞
Question 11
From the above diagram, the cone formed has the form x= y2
Therefore, the volume is given by V =π ∫
x=0
5
y2 dx
But we know that y=2 x so that
V =π ∫
x=0
5
(2 x)2 dx=4 π ∫
x=0
5
x2 dx
V =4 π |x3
3 |0
5
=4 π ( 53
3 )=4 π ( 125
3 )=166.667 π =523.6
Question 12
y=100 sin (2 θ) , 0 ≤ 2θ ≤ π
y RMS= √ 1
π−0 ∫
0
π
y2 dθ
¿ √ 1
π ∫
0
π
104 sin 2 (2 θ)dθ
¿ √ 104
π ∫
0
π
sin 2(2θ) dθ
We can write sin2 ( 2θ ) dθ= 1−cos ( 4 θ)
2 so that
√ 104
π ∫
0
π
sin 2 (2θ)dθ= √ 104
π ∫
0
π
1−cos (4 θ)
2 dθ
¿ √ 104
2 π ∫
0
π
1−cos (4 θ)dθ
¿ √ 104
2 π |θ− 1
4 sin (4 θ)|0
π
¿ √ 104
2 π ¿ ¿
RMS voltage= √ 104
2 π ( π )= √ 104
2 =70.7106V
Question 13
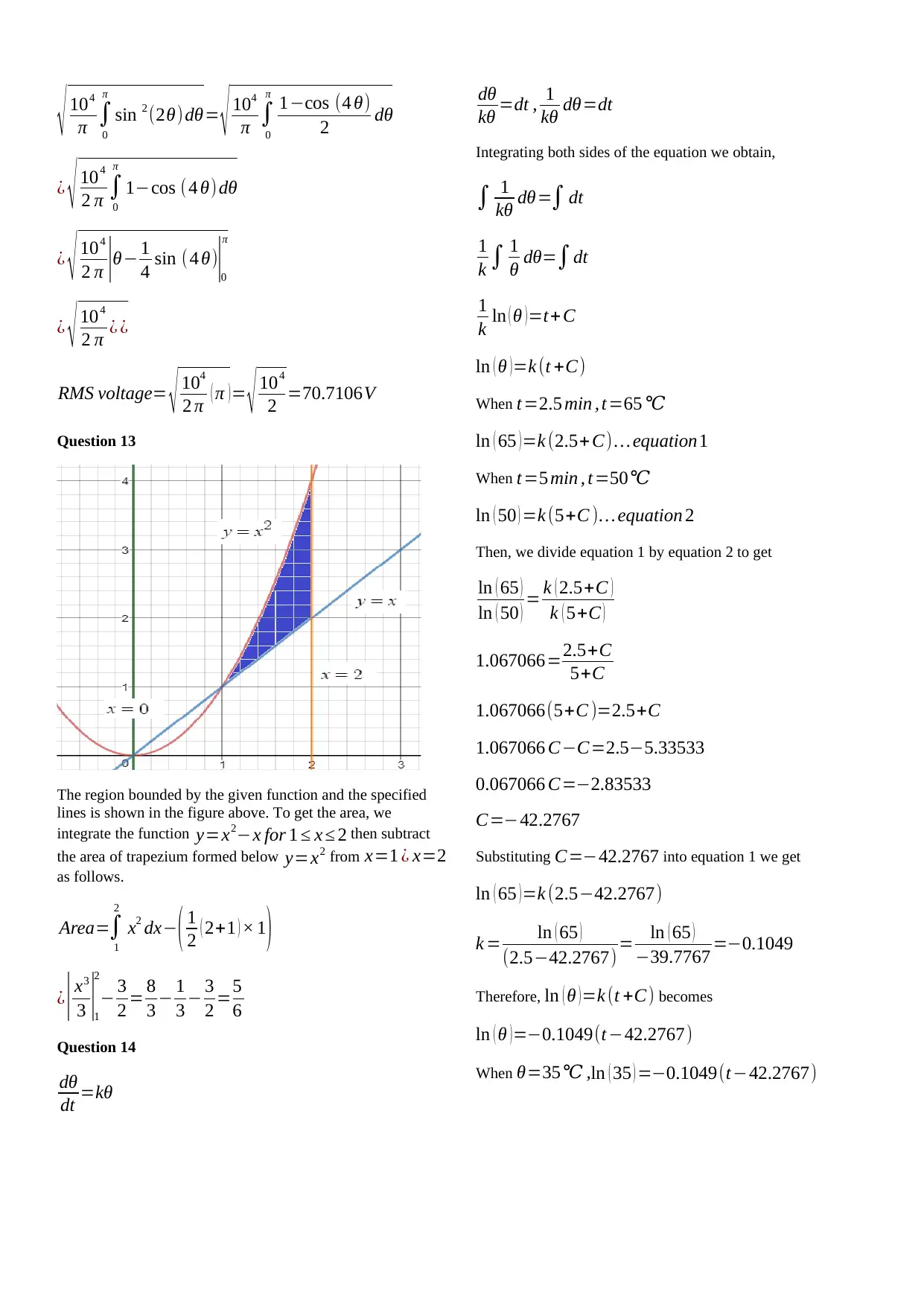
The region bounded by the given function and the specified
lines is shown in the figure above. To get the area, we
integrate the function y=x2−x for 1 ≤ x ≤ 2 then subtract
the area of trapezium formed below y=x2 from x=1 ¿ x=2
as follows.
Area=∫
1
2
x2 dx− ( 1
2 ( 2+1 ) × 1 )
¿| x3
3 |1
2
− 3
2 = 8
3 − 1
3 − 3
2 =5
6
Question 14
dθ
dt =kθ
dθ
kθ =dt , 1
kθ dθ=dt
Integrating both sides of the equation we obtain,
∫ 1
kθ dθ=∫ dt
1
k ∫ 1
θ dθ=∫dt
1
k ln ( θ )=t+C
ln ( θ )=k (t +C)
When t=2.5 min , t=65 ℃
ln ( 65 ) =k (2.5+ C) … equation1
When t=5 min , t=50℃
ln ( 50 ) =k (5+C )… equation 2
Then, we divide equation 1 by equation 2 to get
ln ( 65 )
ln ( 50 ) = k ( 2.5+C )
k ( 5+C )
1.067066=2.5+C
5+C
1.067066(5+C )=2.5+C
1.067066 C−C=2.5−5.33533
0.067066 C=−2.83533
C=−42.2767
Substituting C=−42.2767 into equation 1 we get
ln ( 65 ) =k (2.5−42.2767)
k = ln ( 65 )
(2.5−42.2767)= ln ( 65 )
−39.7767 =−0.1049
Therefore, ln ( θ )=k (t +C) becomes
ln ( θ ) =−0.1049(t−42.2767)
When θ=35℃ ,ln ( 35 ) =−0.1049(t−42.2767)
π ∫
0
π
sin 2 (2θ)dθ= √ 104
π ∫
0
π
1−cos (4 θ)
2 dθ
¿ √ 104
2 π ∫
0
π
1−cos (4 θ)dθ
¿ √ 104
2 π |θ− 1
4 sin (4 θ)|0
π
¿ √ 104
2 π ¿ ¿
RMS voltage= √ 104
2 π ( π )= √ 104
2 =70.7106V
Question 13
The region bounded by the given function and the specified
lines is shown in the figure above. To get the area, we
integrate the function y=x2−x for 1 ≤ x ≤ 2 then subtract
the area of trapezium formed below y=x2 from x=1 ¿ x=2
as follows.
Area=∫
1
2
x2 dx− ( 1
2 ( 2+1 ) × 1 )
¿| x3
3 |1
2
− 3
2 = 8
3 − 1
3 − 3
2 =5
6
Question 14
dθ
dt =kθ
dθ
kθ =dt , 1
kθ dθ=dt
Integrating both sides of the equation we obtain,
∫ 1
kθ dθ=∫ dt
1
k ∫ 1
θ dθ=∫dt
1
k ln ( θ )=t+C
ln ( θ )=k (t +C)
When t=2.5 min , t=65 ℃
ln ( 65 ) =k (2.5+ C) … equation1
When t=5 min , t=50℃
ln ( 50 ) =k (5+C )… equation 2
Then, we divide equation 1 by equation 2 to get
ln ( 65 )
ln ( 50 ) = k ( 2.5+C )
k ( 5+C )
1.067066=2.5+C
5+C
1.067066(5+C )=2.5+C
1.067066 C−C=2.5−5.33533
0.067066 C=−2.83533
C=−42.2767
Substituting C=−42.2767 into equation 1 we get
ln ( 65 ) =k (2.5−42.2767)
k = ln ( 65 )
(2.5−42.2767)= ln ( 65 )
−39.7767 =−0.1049
Therefore, ln ( θ )=k (t +C) becomes
ln ( θ ) =−0.1049(t−42.2767)
When θ=35℃ ,ln ( 35 ) =−0.1049(t−42.2767)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

ln ( 35 )
−0.1049 =(t−42.2767)
−33.878044=t−42.2767
t=42.2767−33.878044=8.398656 minutes
t= ( 8.398656 ×60 ) s=503.91936
t ≅ 504 seconds
−0.1049 =(t−42.2767)
−33.878044=t−42.2767
t=42.2767−33.878044=8.398656 minutes
t= ( 8.398656 ×60 ) s=503.91936
t ≅ 504 seconds
1 out of 7
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.



