Math 202: Calculus Homework 3 - Mean Value Theorem and Integrals

This document presents a comprehensive solution to a Calculus II homework assignment. The solution begins with a proof of the Mean Value Theorem for double integrals, leveraging the Extreme Value Theorem. Following this, the assignment addresses the calculation of the average distance from points within a disk to the origin, employing polar coordinates for simplification. The solution then delves into improper integrals of two-variable functions over the entire plane, utilizing disks and exploring limits to evaluate the integrals. Specific examples involving the function e^(-(x^2 + y^2)) are analyzed, and the solution demonstrates the application of Fubini's Theorem and the conversion to polar coordinates to solve these types of problems. Finally, the solution explores the advantages of function notation and calculates the average value of a function over a cube and a hemisphere, utilizing triple integrals and spherical coordinates.

Proof
Let f (x, y) be a continuous realvalued function D be a closed,connected
region, that has area A(D).
We first state the Extreme Value Theorem for function in two variables:
According to B,Hass,Heil and Weir (2018),“Let f (x, y) be a continuous
function.If D is a closed and bounded region then there exists (x1, y1),(x2, y2)
∈ D such that f (x1, y1) is an absolute maximum of f and f (x2, y2) is an ab-
solute minimum of f .”
Thus, by Extreme Value Theorem
f (x1, y1) ≤ f (x, y) ≤ f (x2, y2) (1)
Integrating (1) over D
ZZ
D
f (x1, y1) dA ≤
ZZ
D
f (x, y) dA ≤
ZZ
D
f (x2, y2) dA
[
ZZ
D
dA = A(D)]
∴ A(D)f(x 1, y1) ≤
ZZ
D
f (x, y) dA ≤ A(D)f (x2, y2)
[Divide throughout by A(D)]
1

f (x1, y1) ≤ 1
A(D)
ZZ
D
f (x, y) dA ≤ f (x2, y2)
According to B,Hass,Heil and Weir (2018),“By Intermediate Value The-
orem,a continuous function f (x, y) on D,takes every value between it’s
maximum and minimum,therefore,there must a point (x0, y0) ∈ D, such
that”
f (x0, y0) = 1
A(D)
ZZ
D
f (x, y) dA
Multiplying throughout by A(D)
ZZ
D
f (x, y) dA = f (x0, y0) A(D)
which is the Mean Value Theorem in two variables.Hence proved.
Answer
A disk D centered at origin with radius a is shown in figure-1 below.
Figure 1:Disk at origin with radius=a
2

Consider any point P (x, y) which lies inside D.Its distance from the origin
O is given by
d(x, y) =
p x2 + y2
Average value of a function f (x, y) over a bounded region R in the xy- plane
is calculated using formula
f ave = 1
A(R)
ZZ
R
f (x, y) dA (1)
where, A(R) is the area of R.
Area of disk D is:A(D) = πr2 = πa2.
Therefore, by (1), average distance of points in D from origin O is
dave = 1
A(D)
ZZ
D
d(x, y) dA
= 1
π a2
ZZ
D
p x2 + y2 dA
For convenience, switch to polar coordinates (r, θ).
x = r cos θ,y = r sin θ
Area element of a disk is given by:dA = rdrdθ.
In the region D, r varies from 0 to a while θ varies from 0 to 2π.Therefore,
dave = 1
π a2
ZZ
D
√ r2 rdrdθ
[Applying limits to the integral]
= 1
π a2
Z 2π
0
Z a
0
r2 drdθ
= 1
π a2
Z 2π
0
r3
3
a
0
dθ
3

= 1
π a2
Z 2π
0
a3
3 dθ
= a
3π
Z 2π
0
dθ
= a
3π 2π
∴ dave = 2a
3
Thus, the average value of distance of points from origin, in a disk centered
at origin with radius a is
2a
3 .
4

Answer
a)
5

ZZ
R2
f (x, y) dA = lim
a→∞
ZZ
aD
f (x, y) dA
where, aD is a disk centered at origin with radius = a.
Let,
f (x, y) = e−(x2+y2)
Implies,
ZZ
R2
e−(x2+y2) dA = lim
a→∞
ZZ
aD
e−(x2+y2) dA (1)
In order to evaluate the right side of (1), we switch to polar coordinates
(r, θ) in aD and then take the limit of the evaluated integral.
x = r cos θ,y = r sin θ [0 ≤ r ≤ a,0 ≤ θ ≤ 2π]
Area element of the disk is given by:dA = rdrdθ.Therefore,
ZZ
aD
e−(x2+y2) dA =
ZZ
D
e−r 2
· rdrdθ
[Applying Limits]
=
Z 2π
0
Z a
0
re−r2
drdθ
[Substitute:− r2 = t]
=
Z 2π
0
dθ
Z a
0
−1
2et dt
= −1
2
Z 2π
0
dθ
h
e−r2 i a
0
6

= −1
2(e−a2
− 1)
Z 2π
0
dθ
∴
ZZ
aD
e−(x2+y2) dA = −π(e−a2
− 1)
Taking the limit to evaluate the improper integral
ZZ
R2
e−(x2+y2) dA = lim
a→∞ −π(e−a2
− 1)
= lim
a→∞ π − lim
a→∞ πe−a2
= π − 0
∴
ZZ
R2
e−(x2+y2) dA = π
b)
An equivalent definition is given by
ZZ
R2
e−(x2+y2) dA = lim
a→∞
ZZ
aS
e−(x2+y2) dA (2)
where, aS is a square with vertices (±a, ±a).
Within aS,x varies from −a to +a and y also varies from −a to +a.Area
element of square is given by:dA = dxdy.Therefore, applying limits
lim
a→∞
ZZ
aS
e−(x2+y2) dA = lim
a→∞
Z +a
−a
Z +a
−a
e−x2
e−y2
dxdy
[Integral in (2) is equal to π]
[Using Fubini’s Theorem Corollary (B, Hass, Heil and Weir, 2018)]
7

∴ π = lim
a→∞
Z +a
−a
e−x2
dx
Z +a
−a
e−y2
dy
[Taking limit to each integral]
π = lim
a→∞
Z +a
−a
e−x2
dx lim
a→∞
Z +a
−a
e−y2
dy
[As both terms on the right together converge to π,
limit of each term exists and is finite ]
[Applying limit to each integral]
π =
Z +∞
−∞
e−x2
dx
Z +∞
−∞
e−y2
dy
c)
From (b) we have
Z +∞
−∞
e−x2
dx
Z +∞
−∞
e−y2
dy = π (3)
The two integrals on the left in (3) are the same except being expressed in
different variables.Therefore they must be equal.
This implies,
Z +∞
−∞
e−x2
dx
Z +∞
−∞
e−y2
dy =
Z +∞
−∞
e−x2
dx
Z +∞
−∞
e−x2
dx
8

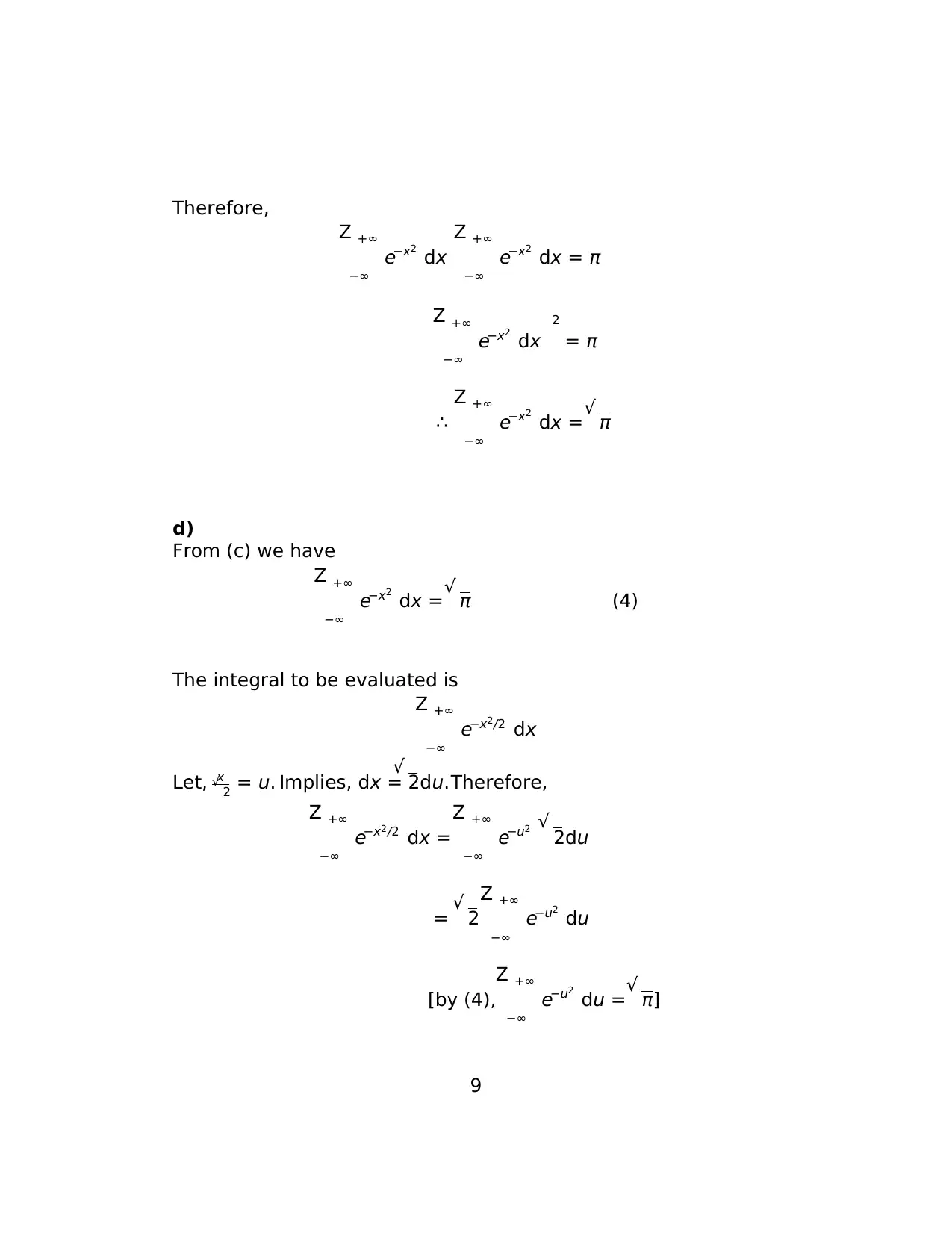
Therefore,
Z +∞
−∞
e−x2
dx
Z +∞
−∞
e−x2
dx = π
Z +∞
−∞
e−x2
dx
2
= π
∴
Z +∞
−∞
e−x2
dx =√ π
d)
From (c) we have
Z +∞
−∞
e−x2
dx =√ π (4)
The integral to be evaluated is
Z +∞
−∞
e−x2/2 dx
Let, x√ 2 = u. Implies, dx =
√ 2du.Therefore,
Z +∞
−∞
e−x2/2 dx =
Z +∞
−∞
e−u2 √ 2du
= √ 2
Z +∞
−∞
e−u2
du
[by (4),
Z +∞
−∞
e−u2
du =√ π]
9

∴
Z +∞
−∞
e−x2/2 dx =√ 2π
Answer
There are two main advantages to the function notation f :D → R com-
pared to the textbook notation f (x, y, z):
1. f : D → R, packs the information about domain of the function which
cannot be conveyed in the other notation.Functions, at times, have meaning
only within a certain set of inputs (domain).Like in this notation it is clearly
indicated that f is defined over the domain D.
2. f : D → R, also indicates the set to which the function maps the inputs.
Like for the given notation it is understood that f maps D to a set of real
numbers R.A function g may map D to a set ofcomplex numbers which
then is denoted as g :D → C. The textbook notation does not carry this
information.
10

Answer
a)
E is a cube with side length equal to L.Therefore, its volume
V (E) = L3
One ofthe vertex ofthe cube lies at the origin and the edges ofcube are
all in the first quadrant,parallelto the coordinate axes.This construction
describes a cube occupying region with limits:0 ≤ x ≤ L, 0 ≤ y ≤ L, 0 ≤
z ≤ L.
Given function is
f (x, y, z) = xyz
Average value of f over E is given by the formula
f ave = 1
V (E)
ZZZ
E
f (x, y, z) dV
Therefore,
f ave = 1
L 3
ZZZ
E
xyz dV
[Applying limits]
= 1
L 3
Z L
0
Z L
0
Z L
0
xyz dxdydz
= 1
L 3
Z L
0
x dx
Z L
0
y dy
Z L
0
z dz
[but,
Z L
0
x dx =
Z L
0
y dy =
Z L
0
z dz]
∴ = 1
L 3
Z L
0
x dx
3
11

= 1
L 3
x2
2
L
0
! 3
∴ f ave = 1
L 3 · L 6
8 = L 3
8
b)
Height of points in a solid hemisphere is given by the function
f (x, y, z) = z
Average height of points over the hemisphere is obtained using the formula
f ave = 1
V (E)
ZZZ
E
f (x, y, z) dV
E is a hemisphere defined as:x2 + y2 + z2 ≤ 1 z ≥ 0, which implies E is
centered at origin with radius = 1 and lies above the plane z = 0.
Volume of E is calculated as
V (E) = 1
2 × 4
3π r3 = 2π
3
Average height is therefore obtained as
f ave = 3
2π
ZZZ
E
z dV
For convenience, switch to spherical coordinates r, θ, φ over E:
x = r cos θ sin φ,y = r sin θ sin φ,z = r cos φ
Within E, r, θ and φ vary as:0 ≤ r ≤ 1, 0 ≤ θ ≤ 2π and 0 ≤ φ ≤ π/2.
Elemental volume of a sphere is:dV = r2 sin φ dφdrdθ.
12

Therefore,
f ave = 3
2π
ZZZ
E
r cos φ · r2 sin φ dφdrdθ
[Trig. Identity:cos x sin x =
sin 2x
2 ]
= 3
2π
ZZZ
E
r3
2 sin (2φ) dφdrdθ
[Applying Limits]
= 3
4π
Z 2π
0
Z 1
0
Z π/2
0
r3 sin (2π) dφdrdθ
= 3
4π
Z 2π
0
Z 1
0
r3 −cos (2φ)
2
π/2
0
drdθ
= 3
4π
Z 2π
0
Z 1
0
r3 drdθ
= 3
4π
Z 2π
0
r4
4
1
0
dθ
= 3
16π
Z 2π
0
dθ = 3
16π× 2π =3
8
Thus the average height of all the points in the hemisphere E is
3
8.
13

References:
B, G., Hass, J., Heil, C. R.,Weir, M. D. (2018).Thomas’ Calculus:Multi-
variable.Boston:Pearson.
Zill, D. G., Wright,W. S. (2011).Multivariable Calculus.Sudbury,Mass:
Jones and Bartlett Publishers.
14