Calculus Quiz 7: Integration, Series, and Limits - Detailed Solutions

This document provides detailed solutions to Calculus Quiz 7. The quiz includes problems on finding the area of a region bounded by a graph, calculating the volume of a solid of revolution, determining the convergence and value of an improper integral, evaluating indefinite and definite integrals, solvi...Read More

QUIZ # 7 Problems
(10 questions, 10 points each)
1. Find the area of the region bounded by the graph of
f ( x )=2 x2+8∧g ( x )=4 x +14 , at the intervale[−3 , 6]
Solution – Area of region bounded by the graph is given by,
∫
a
b
|f ( x ) −g ( x )| dx
f ( x ) =2 x2+ 8
g ( x )=4 x+14
Therefore, Area, A = ∫
−3
6
|2 x2+ 8−4 x+14|dx
Solving the integral, we get A = 290/3 = 96.67
2. Find the volume of the solid generated by rotating the region bounded by y=4 x−x2
about the line x=5.
Solution –
Given equation, y=4 x−x2
About the line x = 5 means x = 0 to 5
Volume =
= 130.9
3. Determine if the improper integral converges and, if so, determine its value: ∫
0
8
1
3
√8−x dx
Solution –
The problem point is the upper limit
Solving for,

∫
0
t
1
3
√8−x dx = −3(8−t )
2
3
2 +6
Now Solving for,
lim
t →8
−3 (8−t )
2
3
2 +6 = 1.61
The limit exists and is finite and so the integral converges and the integral's value is 1.61
4. Evaluate the indefinite integral ∫ xln ( x ) dx
Solution –
Applying Integration by parts,
u = ln x and v = x
Solving, ∫ x
2 dx = x2
4
Therefore, ∫ xln ( x ) dx
5. Evaluate ∫
1
3
4 x2 +5
√ x dx
Solution: Applying Integration by parts
u = 4 x2 +5 and v = 1
√x
Simplifying,

Substituting in the above equation,
Computing for boundaries
Plugging in x = 1
= 58
5
And,
Substituting all the values,
= 30.66
6. A force of 10 lbs is required to hold a spring stretches 4 inches beyond its natural length.
How much work is done to stretches it from its natural length to 5 inches beyond its
natural length?
Solution –
Force = kx
10 = k (1/3) [4 inches = 1/3 feet]
K = 30
So, f (x) = 30x
Work done W = ∫
0
0.416667
30 x dx = 30[ x2
2 ¿ = 30 0.4166672
2
= 2.6 ft.lb
7. Integrate ∫ e3 x
e6 x +36 dx

Solution: ∫ e3 x
e6 x +36 dx
Consider u = 3x
∫ eu
3(e¿¿ 2 u+36) du ¿
Applyingu substitution , v =¿ eu
Applying Integral Substitution, v = 6w
Taking the constant out,
= 1
3 . 1
6 tan−1 w
= 1
3 . 1
6 tan−1 e3 x
6
Therefore, ∫ e3 x
e6 x +36 dx = 1
18 tan−1 1
6 e3 x
+ C
8. Find the interval of convergence for the power series ∑
n =1
∞ 1
2 n+2 xn+2
Solution:
Using the ratio test to find the interval of convergence,
We know that,
Therefore,
Finding,

Simplifying,
Therefore,
Also,
= 1
= |x|
The sum converges for L < 1, therefore solve |x| < 1
For x = 1, there cannot be found a number N which satisfy Cauchy condition, hence it
diverges
For x = -1
= 0 (Converges)
Therefore, the interval of convergence for the power series ∑
n =1
∞ 1
2 n+2 xn+2 = -1 ≤ x < 1
9. Does the series ∑
n=0
∞
( −1 ) n x4 n
n ! converges and, if so to what?
Solution - Using the ratio test to find the interval of convergence,
We know that,
Therefore,

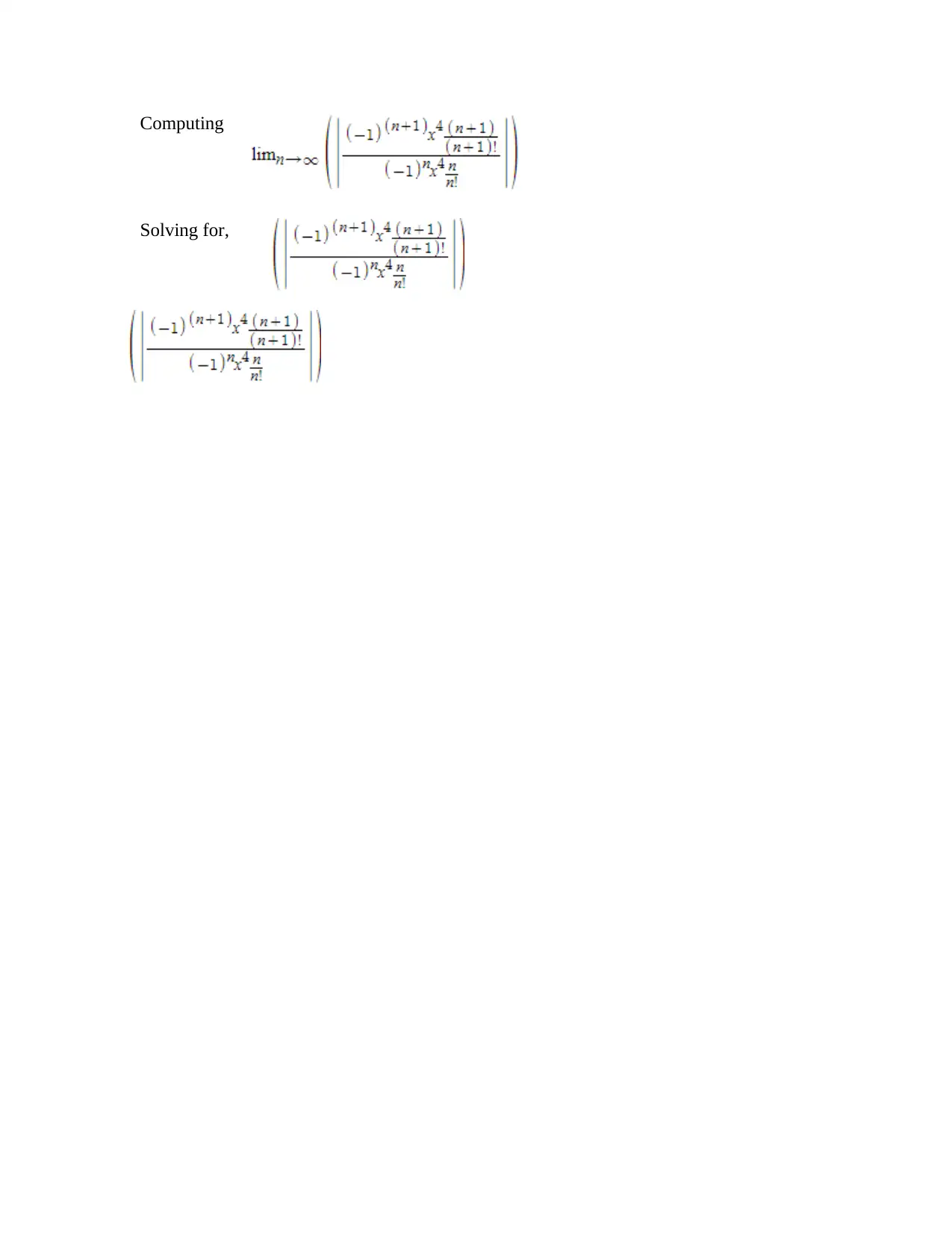
Computing
Solving for,

= −1
n
= 0
L < 1 for every x, therefore ∑
n=0
∞
( −1 ) n x4 n
n ! Converges for all values of x
10. Use a series to evaluate the limit lim
x →0
sin ( x )−x + 1
6 x3
x5
Applying L Hospital Rule
Applying L Hospital Rule
Applying L Hospital Rule
Applying L Hospital Rule