Calculus Assignment: Derivatives, Optimization, Revenue, and Limits

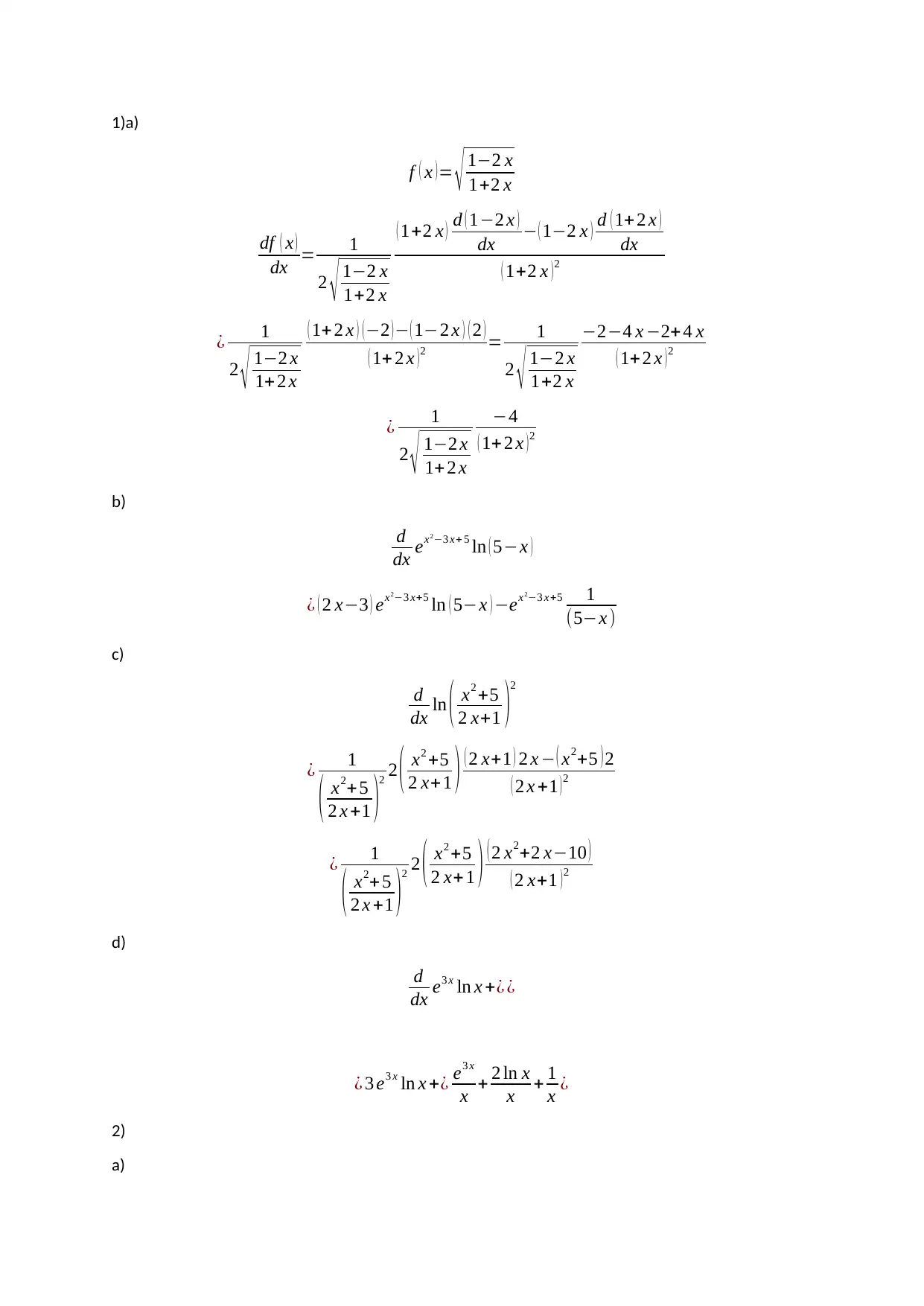
This document presents the solutions to a calculus assignment, covering a range of topics including derivatives, optimization problems, limits, and revenue analysis. The solutions demonstrate the application of differentiation rules to find derivatives of various functions, including those involving square roots, natural logarithms, and exponential functions. The assignment also includes problems on finding the maximum and minimum points of functions using first and second derivatives, determining continuity, and analyzing revenue and profit functions. The solutions involve algebraic manipulations, limit calculations, and the application of calculus concepts to solve practical problems, such as determining the number of units to sell to maximize profit. Furthermore, the assignment explores concepts related to demand functions and their derivatives.

1)a)
f ( x ) = √ 1−2 x
1+2 x
df ( x )
dx = 1
2 √ 1−2 x
1+2 x
( 1+2 x ) d ( 1−2 x )
dx − ( 1−2 x ) d ( 1+ 2 x )
dx
( 1+2 x )2
¿ 1
2 √ 1−2 x
1+ 2 x
( 1+2 x ) (−2 )− ( 1−2 x ) ( 2 )
( 1+ 2 x )2 = 1
2 √ 1−2 x
1+2 x
−2−4 x −2+ 4 x
( 1+ 2 x )2
¿ 1
2 √ 1−2 x
1+ 2 x
−4
( 1+ 2 x ) 2
b)
d
dx ex2−3 x+ 5 ln ( 5−x )
¿ ( 2 x−3 ) ex2−3 x+5 ln ( 5−x ) −ex2−3 x+5 1
(5−x )
c)
d
dx ln ( x2 +5
2 x+1 )2
¿ 1
( x2+5
2 x +1 )2 2 ( x2 +5
2 x+1 ) ( 2 x+1 ) 2 x − ( x2+5 ) 2
( 2 x +1 )2
¿ 1
( x2+ 5
2 x +1 )2 2 ( x2 +5
2 x+ 1 ) ( 2 x2+2 x−10 )
( 2 x+1 )2
d)
d
dx e3 x ln x +¿ ¿
¿ 3 e3 x ln x +¿ e3 x
x + 2 ln x
x + 1
x ¿
2)
a)

lim
h→ 0
−5
x (x +h)=−5
x2
b)
lim
x→ ∞
x3 −5 x2 +8
4 x3−2 x +9
Dividing by x3 both numerator∧denominator
lim
x→ ∞
1− 5
x + 8
x3
4− 2
x2 + 9
x3
= 1
4
c)
i) Yes both left hand limit and right hand limit exists
lim
x →3
( 2 x +3 )=9
ii)
Since lim
x →3
f ( x ) ≠ f ( 3 )
It is not continuous at x = 3.
3)
a)
f ( x )=x3−3 x +2
f ' (x)=3 x2−3
f ' ' ( x ) =6 x
b)
f ' ( x )=3 x2−3=0
x2−1=0=¿ x=± 1
c)
At x = 1
f '' ( x )=6 >0
So, x = 1 is a point of minimum
At x = -1
f '' ( x )=−6<0

So, x = -1 is a point of maximum,
d)
(-1, 4) is the point of maximum as concluded before and similarly (1, 0) is the point of minimum.
4)
a)
Total revenue = (1000 – x) *x
Profit = Total Revenue – Cost
P ( x ) = ( 1000 x−x2 ) −(3000+2 x )
b)
For profit to be maximum,
d
dx P ( x ) =0
d
dx P ( x ) =1000−2 x−2=998−2 x=0=¿ x=499
Therefore 499 units should be sold
c)
P ( 499 ) =998 ( 499 ) −4992−3000=246001

5)
a)
d x
dp =−0.3 p
b) At p = 30,
325−0.15 p2
325−0.15 ( 30 ) 2=190
c)
325−0.15 p2> 0
p< 46.55
The price should be increased till 46