Car Insurance Fraud: Claims Prediction and Data Analysis Project

This project investigates car insurance fraud using a dataset of 1000 claimants. The study examines the relationship between individual claims (injury, property, vehicle) and total claim amounts. It explores the use of clustering, classification, and linear regression models to predict total claims based on attributes like age, policy deductibles, and premiums. The analysis includes correlation coefficients and visualizations using Tableau and R, revealing insights into claim trends. The project aims to assist insurance companies in making informed decisions about reserving, premium calculations, and policy deductibles, as well as identifying potential fraud. The findings highlight the importance of understanding the relationships between various claim types and their impact on overall claim amounts, with the goal of developing models to predict total claims and detect anomalies indicative of fraudulent activities. The project's methodology includes data preparation, model generation, and testing, with an emphasis on linear regression for prediction.

CAR INSURANCE FRAUD
1
CAR INSURANCE FRAUD
Name of institution:
Name of student:
Date:
Word count: 2157

CAR INSURANCE FRAUD
2
Section 1: The Problem
The amount the client of insurance companies (insured/assured) pay in order to be compensated
in the event of risk is known as the premium. Therefore, the amount of premium is equivalent to
the cost of getting an insurance cover or policy. An insurance cover or an insurance policy is the
contract binding the insured/assured and the insurance company. An insurance policy usually
comes with policy deductibles (Valles-Barjas & Fernando, 2015).
. A policy deductible is the amount of money that is being deducted from the premium for the
purpose of policy administrations. All these factors influences the total claim amounts as well as
the amount of individual claims.
An insurance claim that has been made in contrary to the agreements in the contract is an
insurance fraud. A fraud in insurance may result from numerous sources. The major cause of
insurance fraud is the collision between the insurance officers and the insured person. When an
insurance fraud occurs, the insurance company may experience a loss or reduction in the profits.
An insurance fraud may also result into increase in the total claims that the insurance pays.
Given the total claim amount, the individual claim amounts, the premiums and the policy
deductibles, an insurance company has a problem of maintaining sufficient amount of money
that can be used to settle the claims at any given time. The practice of maintaining sufficient
amount of money for insurance operations and claim compensations is known as reserving. The
problem that this study addresses is to investigate the relationship between individual claims and
the total claim amounts. The establishment of the relationship will help the insurance companies
to in making informed decisions about reserving, premium calculations and policy deductibles.
Therefore, the research question is: Can we establish the relationship between the total claims

CAR INSURANCE FRAUD
3
and individual claim amounts? Can we use individual claim amounts, policy deductibles and
premiums to predict the expected total claims of an insurance company at any given time?
The establishment of the relationship between individual claims and the total claims will help the
management of the insurance company to identify the anomalies in case an insurance fraud has
occurred. Therefore, if a model of predicting the total premiums is determined, the management
of the insurance company can use it to determine and investigate unusual total claims at any
given time.
The decision maker of the research problem being addressed in this study is the management of
insurance companies. The management of the insurance companies have the responsibility of
ensuring that the company has sufficient funds/reserves for settling claims at any given time.
The data that have been used for analysis is a secondary data. The data was collected from the
previous records of insurance data. The data is reliable data since it contains the previous records
that were recorded on real time. The information is about the individual insurance claims of
difference categories, the date of policy, the premium amounts, policy deductibles and the total
claims. The target attributes of the data include the age of the insured/assured, the total claims,
policy deductibles, and the amount of premium, injury claims, property claims and vehicle
claims. I have chosen the target attributes since they directly determine the total claims and the
amount of reserves that the insurance company will hold at any given time.
Section 2: Understand the Data
The original dataset consisted of both numerical and categorical (qualitative data). The
categorical data that was present in the data was claim category and the sex of the clients
(insured persons). The original data set consisted of 1000 data points representing 1000

CAR INSURANCE FRAUD
4
claimants during the period. The sample data that have been used for analysis consists of 8
attributes: The age of the insured, the amount of policy deductible, the amount of injury claims,
the amount of property claims, the amount vehicle claims, the premium and the amount of total
claims. The eight attributes were the most relevant attributes for this study.
The amount of vehicle claim, the amount of property claims and the amount of injury claims are
relevant for this study because they represents individual claims (An Creemers, et al., 2012). Total
claims amount is relevant because it represents the pool of all claims that an insurance company
pays to the insured. Policy deductible is relevant to this study because it directly affects the value
of total claims as well as the amount of reserves the insurance company will pay to the insured.
The eight attributes are all quantitative in nature. Similarly, the eight attributes are all numerical
in nature and can be quantified in terms of numbers.
correlation1<-cor(total_claims,Vehicle_claim,method = "kendal")
> correlation1
[1] 0.8522978
The output above shows that total claim amounts and vehicle claims are correlated. The
correlation coefficient is 0.8522 implying a strong positive correlation coefficient (Zou, et al.,
2013). The strong positive correlation implies that an increase in the amount of vehicle claims by
1 unit will cause a corresponding increase in the amount of total claims by 0.8522 units (Bolin &
Jocelyn, 2014).
> correlation2<-cor(total_claims,injury_claim,method = "kendall")
> correlation2
[1] 0.6330977
The correlation coefficient between total claims and injury claims is 0.6330977. The correlation
is a strong positive correlation (Chehreh, et al., 2010). The correlation implies that an increase in
the value of injury claims by 1 unit will cause a corresponding increase in the amount of total
claims by 0.6330 units (Xia, et al., 2013).

CAR INSURANCE FRAUD
5
> correlation3<-cor(total_claims,property_claim)
> correlation3
[1] 0.8106865
The correlation coefficient between property claims and the total claims is 0.8106865. The
correlation coefficient is a strong positive correlation coefficient (Federico, et al., 2009). The
correlation coefficient implies that an increase in the value of total claims by 1 will cause a
corresponding increase in the value of property claims by 0.8106865 (Valles-Barjas & Fernando,
2015).
> correlation4<-cor(total_claims,age, method = "kendall")
> correlation4
[1] 0.04370292
The above output implies that the correlation coefficient between the amount of total claims and
the age of an insured is 0.04370 (Jieli, et al., 2012). The correlation is a weak correlation
coefficient. The correlation implies that an increase in the value of the age of an insured by 1 unit
will cause a corresponding increase in the value of total claims by 0.04370 units (Sungduk, et al.,
2011).
> correlation5<-cor(total_claims,Policy_Deductible, method = "kendall")
> correlation5
[1] 0.01577333
The correlation coefficient between the amount of policy deductible and the amount of total
claims is 0.01577. The correlation is a weak positive correlation (Jieli, et al., 2012). The correlation
implies that an increase in the value of policy deductible by 1 unit will cause a corresponding
increase in the value of total claims by 0.0157733 (Richard, 2009).
> correlation6<-cor(total_claims,annual_premium,method="kendall")
> correlation6

CAR INSURANCE FRAUD
6
[1] 0.0002062721
The correlation coefficient between the amount of annual premiums and the amount of total
claims is 0.0002062721 (Levin & Paul, 2016). The correlation is a weak negative correlation. The
correlation coefficient implies that an increase in the value of annual premiums by 1 unit will
cause a corresponding increase in the value of total premiums by 0.0002062721 (Revan, 2009).
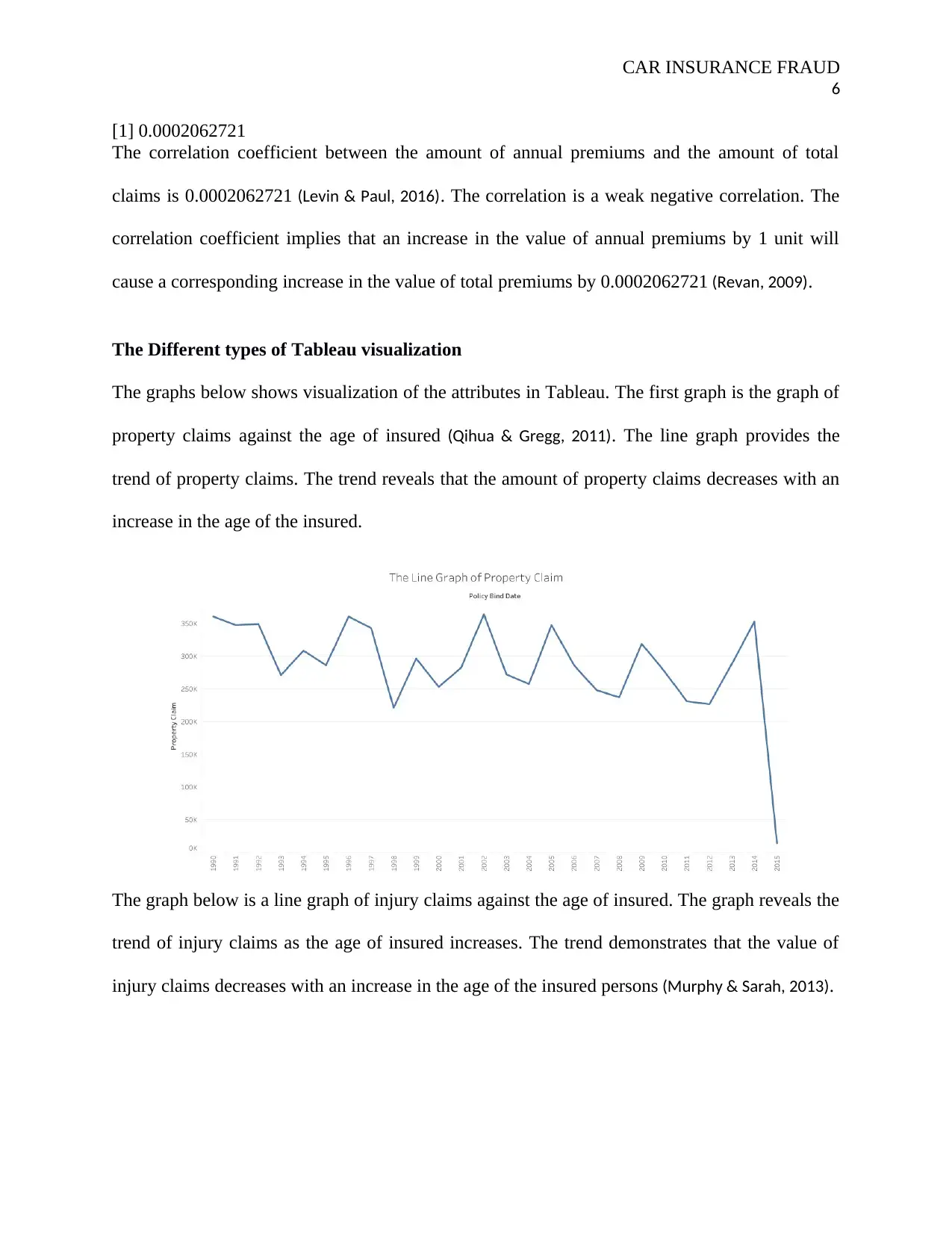
The Different types of Tableau visualization
The graphs below shows visualization of the attributes in Tableau. The first graph is the graph of
property claims against the age of insured (Qihua & Gregg, 2011). The line graph provides the
trend of property claims. The trend reveals that the amount of property claims decreases with an
increase in the age of the insured.
The graph below is a line graph of injury claims against the age of insured. The graph reveals the
trend of injury claims as the age of insured increases. The trend demonstrates that the value of
injury claims decreases with an increase in the age of the insured persons (Murphy & Sarah, 2013).

CAR INSURANCE FRAUD
7
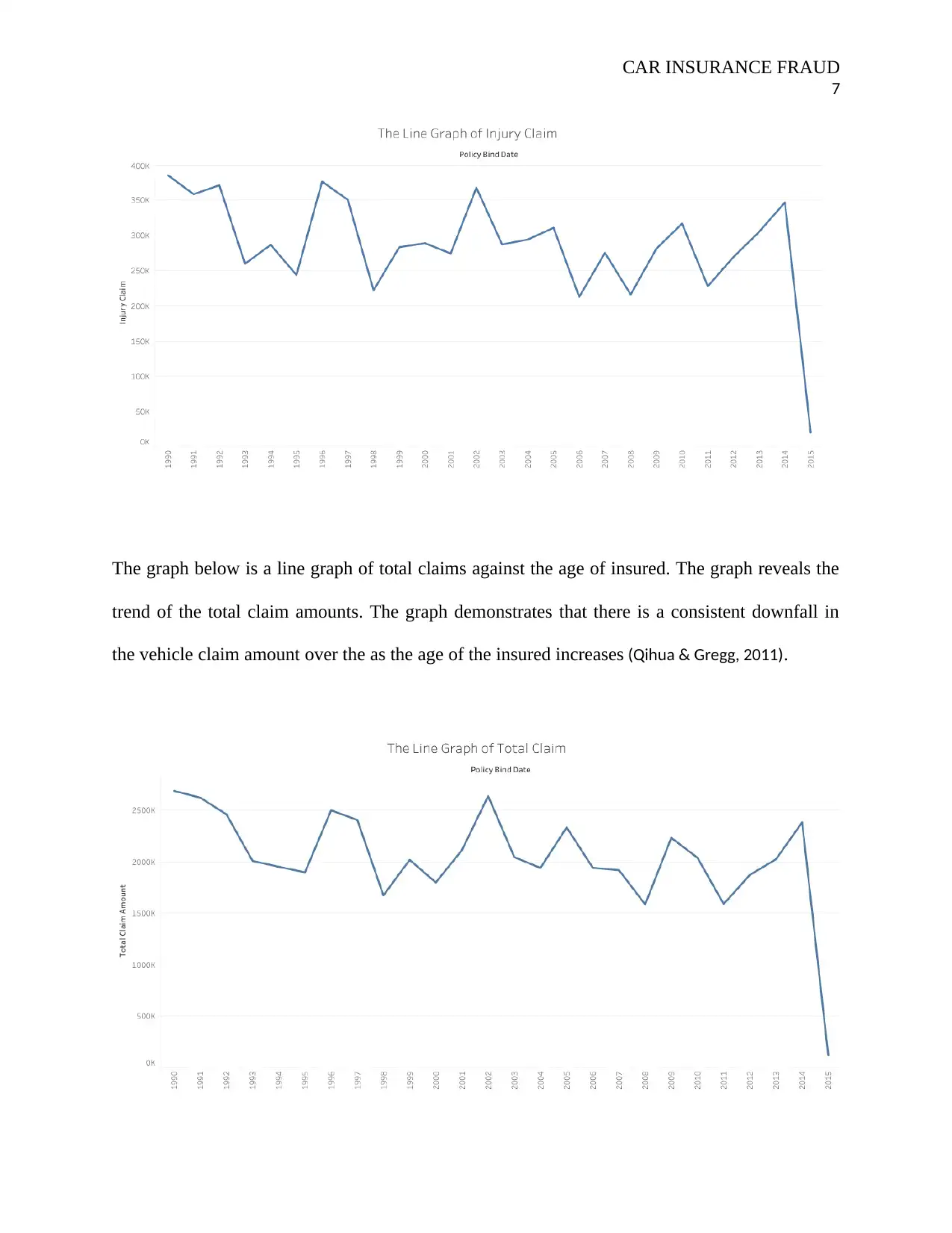
The graph below is a line graph of total claims against the age of insured. The graph reveals the
trend of the total claim amounts. The graph demonstrates that there is a consistent downfall in
the vehicle claim amount over the as the age of the insured increases (Qihua & Gregg, 2011).

CAR INSURANCE FRAUD
8
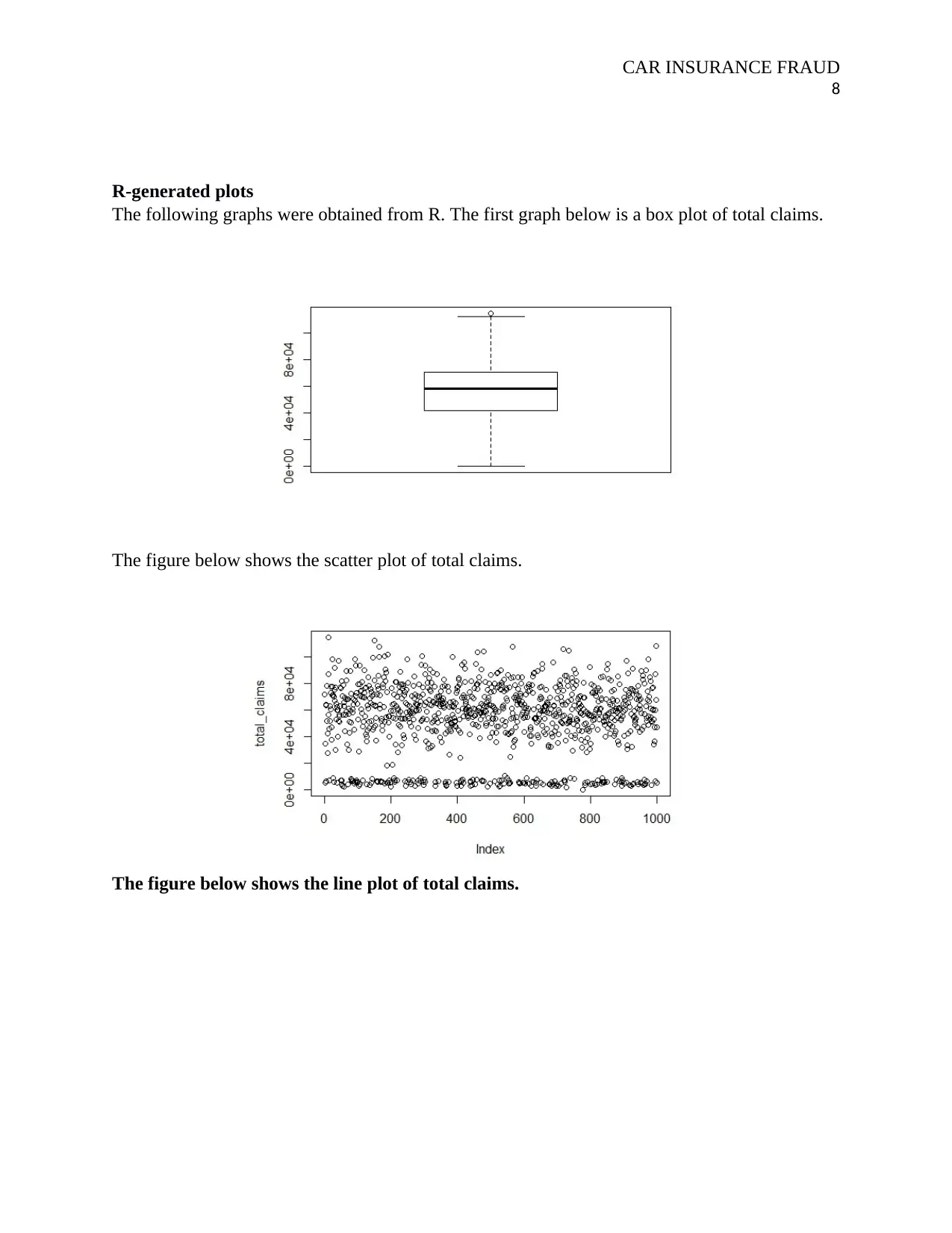
R-generated plots
The following graphs were obtained from R. The first graph below is a box plot of total claims.
The figure below shows the scatter plot of total claims.
The figure below shows the line plot of total claims.

CAR INSURANCE FRAUD
9
The table below was obtained from R:
summary(total_claims,annual_premium,Vehicle_claim,injury_claim,Policy_Deductible,property
_claim)
Min. 1st Qu. Median Mean 3rd Qu. Max.
100 41813 58055 52762 70593 114920
The table reveals that the minimum total claims was 100 while the maximumwas 114920. The
average total claims is 52762.
Section 3: Prepare the Data
The attributes for analysis are: The age of the insured, the annual premium, the amount of policy
deductible, the amount of injury claims, the amount of property claims, the amount of vehicle
claims and the total amount of claims (Niu, et al., 2014). The attributes have been derived or
extracted from the data set using the following steps of codes in R:
#Importing the claims data
Claims_Dataset<-read.csv("F:\\ClaimsData.csv", header = TRUE)

CAR INSURANCE FRAUD
10
#Extracting the age variable from the data set:
age<-Claims_Dataset$age
#Extracting the policy deductible attribute from the claims data:
Policy_Deductible<-Claims_Dataset$policy_deductable
#Extracting the annual premiums attribute from the data set
annual_premium<-Claims_Dataset$policy_annual_premium
#extracting the injury claims attribute
injury_claim<-Claims_Dataset$injury_claim
#Extracting the property claims attribute
property_claim<-Claims_Dataset$property_claim
#Extracting the vehicle claims attribute
Vehicle_claim<-Claims_Dataset$vehicle_claim
#Extracting the Total claims attribute
total_claims<-Claims_Dataset$total_claim_amount
Preparing the test and Training data
The following codes were used to prepare the train sample data sets:
#Data Manipulation
st_X<-Claims_Dataset[,2:8]
st_x1<-scale(st_X)
summary(st_x1)

CAR INSURANCE FRAUD
11
library(class)
n<-nrow(Claims_Dataset)
#train datasets
train_data<-sample(n,0.7*n)
train_X<-st_x1[train_data]
train_Y<-Claims_Dataset[train_data,5]
#test datasets
test_X<-st_x1[-train_data]
test_Y<-Claims_Dataset[-train_data,5]
Section 4: Generate and Test Prediction Models
The models that I have used are: Clustering, classification and regression model. The codes of
classification are shown below.
Clustering
Clustering
hc<-hclust(dist(Claims_Dataset))
hc
library(dendextend)
hc_1<-hclust(dist(Claims_Dataset))
hc_1
dend<-as.dendrogram(hc_1)
dend
dend<-color_labels(dend,2)
dend<-color_branches(dend,2)
plot(dend)
The table below shows the output of summary statistics of the data sets that.
#Data Manipulation

CAR INSURANCE FRAUD
12
> st_X<-Claims_Dataset[,2:8]
> st_x1<-scale(st_X)
> summary(st_x1)
age policy_deductable policy_annual_premium total_claim_amount
Min. :-2.1824 Min. :-1.0394 Min. :-3.370950 Min. :-1.9947
1st Qu.:-0.7602 1st Qu.:-1.0394 1st Qu.:-0.683132 1st Qu.:-0.4147
Median :-0.1037 Median :-0.2223 Median : 0.003251 Median : 0.2005
Mean : 0.0000 Mean : 0.0000 Mean : 0.000000 Mean : 0.0000
3rd Qu.: 0.5527 3rd Qu.: 1.4121 3rd Qu.: 0.652376 3rd Qu.: 0.6754
Max. : 2.7408 Max. : 1.4121 Max. : 3.240334 Max. : 2.3543
injury_claim property_claim vehicle_claim
Min. :-1.5229 Min. :-1.5337 Min. :-2.0046
1st Qu.:-0.6430 1st Qu.:-0.6124 1st Qu.:-0.4043
Median :-0.1349 Median :-0.1346 Median : 0.2209
Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
3rd Qu.: 0.7932 3rd Qu.: 0.7224 3rd Qu.: 0.6827
Max. : 2.8717 Max. : 3.3723 Max. : 2.2043
The figure below shows the dendrogram that has resulted from the clustering.
Classification
#Classification
knn(train_X,test_X,train_Y,k=5)

CAR INSURANCE FRAUD
13
all:
hclust(d = dist(Claims_Dataset))
classification method : complete
Distance : euclidean
Number of objects: 1000
Linear Regression
Linear regression was used to generate a model for predicting the total amount of claims (Pietro &
Rajeev, 2009). The model predicts the total amount of claims given the amount of vehicle claims,
the amount of property claims and the amount of annual premium The R code for generating the
linear model is as shown below:
#Linear Regression
gl_model<-lm(total_claims~Vehicle_claim,injury_claim,property_claim, annual_premium)
summary(gl_model)
The Output of the model is:
Residuals:
Min 1Q Median 3Q Max
-6.3002 -1.6629 0.0412 1.8944 3.9775
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.1509 0.48971 2.897 0.00786 **
x 0.67461 0.05191 12.997 1.16e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared: 0.9548, Adjusted R-squared: 0.9491

CAR INSURANCE FRAUD
14
F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06
The ensemble model:
From the results above, it is possible to obtain the model for predicting the total amount of
claims as:
Total claims= 5.1509(vehicle calims)+ 0.48971(injury calims)+ 2.897(property claims)+
0.00786 (annual premium).
The rules of accuracy of the model is such that the level of significance must be 0.05 and the
degrees of freedom is 8. The rules of accuracy are applicable because the model is a simple
linear model and not a generalized linear model. The model can be improved by incorporating
more attributes such as frequency of individual claims and total claims. The model can also be
improved by making it more generalized (developing a generalized linear model).
Section 5: Problem Conclusions and Recommendations
The correlation coefficient between property claims and the total claims is 0.8106865. The
correlation coefficient is a strong positive correlation coefficient. The correlation coefficient
implies that an increase in the value of total claims by 1 will cause a corresponding increase in
the value of property claims by 0.8106865. The coefficient between the amount of total claims
and the age of an insured is 0.04370. The correlation is a weak correlation coefficient. The
correlation implies that an increase in the value of the age of an insured by 1 unit will cause a
corresponding increase in the value of total claims by 0.04370 units.
The correlation coefficient between the amount of policy deductible and the amount of total
claims is 0.01577. The correlation is a weak positive correlation. The correlation implies that an
increase in the value of policy deductible by 1 unit will cause a corresponding increase in the

CAR INSURANCE FRAUD
15
value of total claims by 0.0157733. The correlation coefficient between the amount of annual
premiums and the amount of total claims is 0.0002062721. The correlation is a weak negative
correlation. The correlation coefficient implies that an increase in the value of annual premiums
by 1 unit will cause a corresponding increase in the value of total premiums by 0.0002062721.
The graphs below shows visualization of the attributes in Tableau. The first graph is the graph of
property claims against the age of insured. The line graph provides the trend of property claims.
The trend reveals that the amount of property claims decreases with an increase in the age of the
insured.
The model for predicting the total amount of claims as:
Total claims= 5.1509(vehicle claims) + 0.48971(injury claims) + 2.897(property claims) +
0.00786 (annual premium).
The model for predicting the total claims at any given point will help the management to keenly
monitor and detect any anomalies in the amount of claims that they pay out. Therefore, if they
experience any unusually large amounts of payments, then they can easily launch investigations
to determine the source of fraud.
The recommendation I would make to my problem’s decision maker is that they can modify the
model to more generalized model that can be used in determining total claims given any set of
individual claims. The reason I would give the recommendation is because the model is more
specific to the individual claims that have been used in building it. Similarly, I would
recommend that the model to be used with annual data only. Therefore, if any case any of the
attributes are collected say in monthly basis, then they have to be converted to annual data. The
reason why I would give the recommendation is because the model has been built on annual data
and hence purely works with annual data.

CAR INSURANCE FRAUD
16
The most important variables that the decision maker should look at are the individual claims
and total claims. Individual clams and total claims are the most important variables because they
are the major indicators of insurance fraud, hence it would be easier to experience a fraud in the
claim process.
References
An Creemers, Marc, A., Niel, H. & Geert, M., 2012. A nonparametric approach to weighted
estimating equations for regression analysis with missing covariates. The Journal of
Computational Statistics & Data Analysis, 56(1), pp. 3-14.
Bolin & Jocelyn, H., 2014. ntroduction to Mediation, Moderation, and Conditional Process
Analysis: A Regression-Based Approach. New York, NY: The Guilford Press. The Journal of
Educational Measurement, 51(3), p. 3.

CAR INSURANCE FRAUD
17
Chehreh, C., Mesroghli, S. & James, C. H., 2010. Simultaneous prediction of coal rank
parameters based on ultimate analysis using regression and artificial neural network.
International Journal of Coal Geology, 83(1), p. 4.
Federico, A., Elia, B. & Patrizia, B., 2009. Estimating crude cumulative incidences through
multinomial logit regression on discrete cause-specific hazards. The Journal of Computational
Statistics & Data Analysis, 53(07), p. 3.
Jieli, D. et al., 2012. Regression analysis for a summed missing data problem under an outcome-
dependent sampling scheme. The Canadian Journal of Statistics, 40(2), p. 2.
Levin & Paul, 2016. Construction Contract Claims, Changes, and Dispute Resolution || Insurance
Issues: Construction Claims of a Different Nature. The Journal of insurance, 10(1), p. 4.
Murphy & Sarah, A., 2013. Data Visualization and Rapid Analytics: Applying Tableau Desktop
to Support Library Decision-Making. The Journal of Web Librarianship, 7(4), pp. 2-9.
Niu, et al., 2014. Empirical likelihood inference in linear regression with nonignorable missing
response. Computational Statistics & Data Analysis, 79(11), pp. 2-7.
Pietro, A. & Rajeev, G., 2009. he Tableau Workbench. Electronic Notes in Theoretical
Computer Science, 23(1), pp. 3-13.
Qihua, W. & Gregg, E. D., 2011. Linear regression analysis of survival data with missing
censoring indicators. TheJournal of Lifetime Data Analysis, 17(2), pp. 3-24.
Revan, M. O., 2009. A stochastic restricted ridge regression estimator. The Journal of
Multivariate Analysis, 100(8), pp. 2-10.
Richard, P. H., 2009. Applied Regression Analysis and Generalized Linear Models. The Journal
of Technometrics, 51(3), pp. 2-10.
Sungduk, K., Ming-Hui, C. & Dipak, K. D., 2011. A new threshold regression model for survival
data with a cure fraction. The Journal of Lifetime Data Analysis, 17(1), pp. 1-9.
Valles-Barjas & Fernando, 2015. A comparative analysis between two techniques for the
prediction of software defects: fuzzy and statistical linear regression. The Journal of Innovations
in Systems and Software Engineering, 11(4), p. 3.
Xia, et al., 2013. A Logistic Normal Multinomial Regression Model for Microbiome
Compositional Data Analysis. The Journal of Biometrics, 69(4), p. 2.
Zou, et al., 2013. Application of finite mixture of negative binomial regression models with
varying weight parameters for vehicle crash data analysis. The Jouranl of Accident Analysis &
Prevention, 50(1), p. 2.

CAR INSURANCE FRAUD
18
Appendix:
The R-Codes
Claims_Dataset<-read.csv("F:\\ClaimsData.csv", header = TRUE)
age<-Claims_Dataset$age
Policy_Deductible<-Claims_Dataset$policy_deductable
annual_premium<-Claims_Dataset$policy_annual_premium
injury_claim<-Claims_Dataset$injury_claim
property_claim<-Claims_Dataset$property_claim
Vehicle_claim<-Claims_Dataset$vehicle_claim
total_claims<-Claims_Dataset$total_claim_amount
plot(total_claims,type = "l", color="Red")
summary(total_claims,annual_premium,Vehicle_claim,injury_claim,Policy_Deductible,p
roperty_claim)
correlation1<-cor(total_claims,Vehicle_claim,method = "kendal")
correlation1
correlation2<-cor(total_claims,injury_claim,method = "kendall")
correlation2
correlation3<-cor(total_claims,property_claim)
correlation3
correlation4<-cor(total_claims,age, method = "kendall")
correlation4
correlation5<-cor(total_claims,Policy_Deductible, method = "kendall")
correlation5
correlation6<-cor(total_claims,annual_premium,method="kendall")
correlation6

CAR INSURANCE FRAUD
19
#Clustering
hc<-hclust(dist(Claims_Dataset))
hc
library(dendextend)
hc_1<-hclust(dist(Claims_Dataset))
hc_1
dend<-as.dendrogram(hc_1)
dend
dend<-color_labels(dend,2)
dend<-color_branches(dend,2)
plot(dend)
#Data Manipulation
st_X<-Claims_Dataset[,2:8]
st_x1<-scale(st_X)
summary(st_x1)
library(class)
n<-nrow(Claims_Dataset)
n
#train datasets
train_data<-sample(n,0.7*n)
train_X<-st_x1[train_data]
train_X
train_Y<-Claims_Dataset[train_data,5]
train_Y
#test datasets
test_X<-st_x1[-train_data]
test_X
test_Y<-Claims_Dataset[-train_data,5]
test_Y
#Classification
knn(train_X,test_X,train_Y,k=5)
#Logistic Regression
gl_model<-
lm(total_claims~Vehicle_claim,injury_claim,property_claim,age,annual_premium,Policy
_Deductible)
summary(gl_model)