Caterpillar Inc. Forklift Production: Profit Maximization Strategy

This assignment focuses on maximizing the profit of Caterpillar Inc. by optimizing the production of four forklift models (W1, W2, W3, and W4) across three assembly departments. The solution employs linear programming techniques and utilizes Excel Solver to determine the optimal production quantities for each forklift model, considering constraints on assembly hours in each stage. The objective function maximizes profit based on the profit contribution of each model. The assignment analyzes decision variables, constraints, and the sensitivity report to understand the impact of changes in profit margins and resource availability. The analysis includes a scenario where the third stage processing time is adjusted to reflect real-world data, and the optimal production plan and maximum profit are recalculated. The findings provide recommendations for production levels to achieve maximum profitability and insights into the sensitivity of the solution to changes in key parameters. The assignment also discusses the impact of setting up a new department. References are included to support the analysis.

EXERCISE QUESTIONS:
a) The objective of the problem is to maximize the profit of Caterpillar Inc. by optimal use of
the capacities in the three departments. The four types of fork lift models that are produced
by CAT are W1,W2,W3 and W4 and each of the fork lift model give 400£,
600£, 300£ and 100£ profit to the company in one month.
Now, let a, b, c and d are the number of fork lift models of W1,W2,W3 and W4 respectively
and these will produce the maximum profit for CAT Inc.
Hence, the objective function will be
Maximize 400*a + 600*b + 300*c+ 100*d
b) The decision variables in the optimization problem are the variables with the optimum
value gives maximum profit. Hence, the number of fork lift models of W1, W2, W3 and W4
which are a, b, c and d are the decision variables.
c) Given that Stage 1 process of assembly has the max limit of 550 hours per month. In stage
1 each unit of W1, W2, W3 and W4 require 1.5 hours, 2 hours, 4 hours and 3 hours
respectively. Stage 2 process of assembly has the max limit 700 hours per month. In stage 2
each unit of W1, W2, W3 and W4 needs 4 hours, 1 hour, 2 hours and 3 hours respectively.
Stage 3 requires total of 200 hours (Vanderbei 2015). In stage 3 each unit of W1, W2, W3
and W4 require 2 hours, 3 hours, 1 hour and 2 hours respectively.
Hence, the constraints of the system in equation form will be,
a*1.5 + b*2 + c*4 + d*3 <= 550
a*4 + b*1 + c*2 + d*3 <= 700
a*2 + b*3 + c*1 + d*2 <= 200

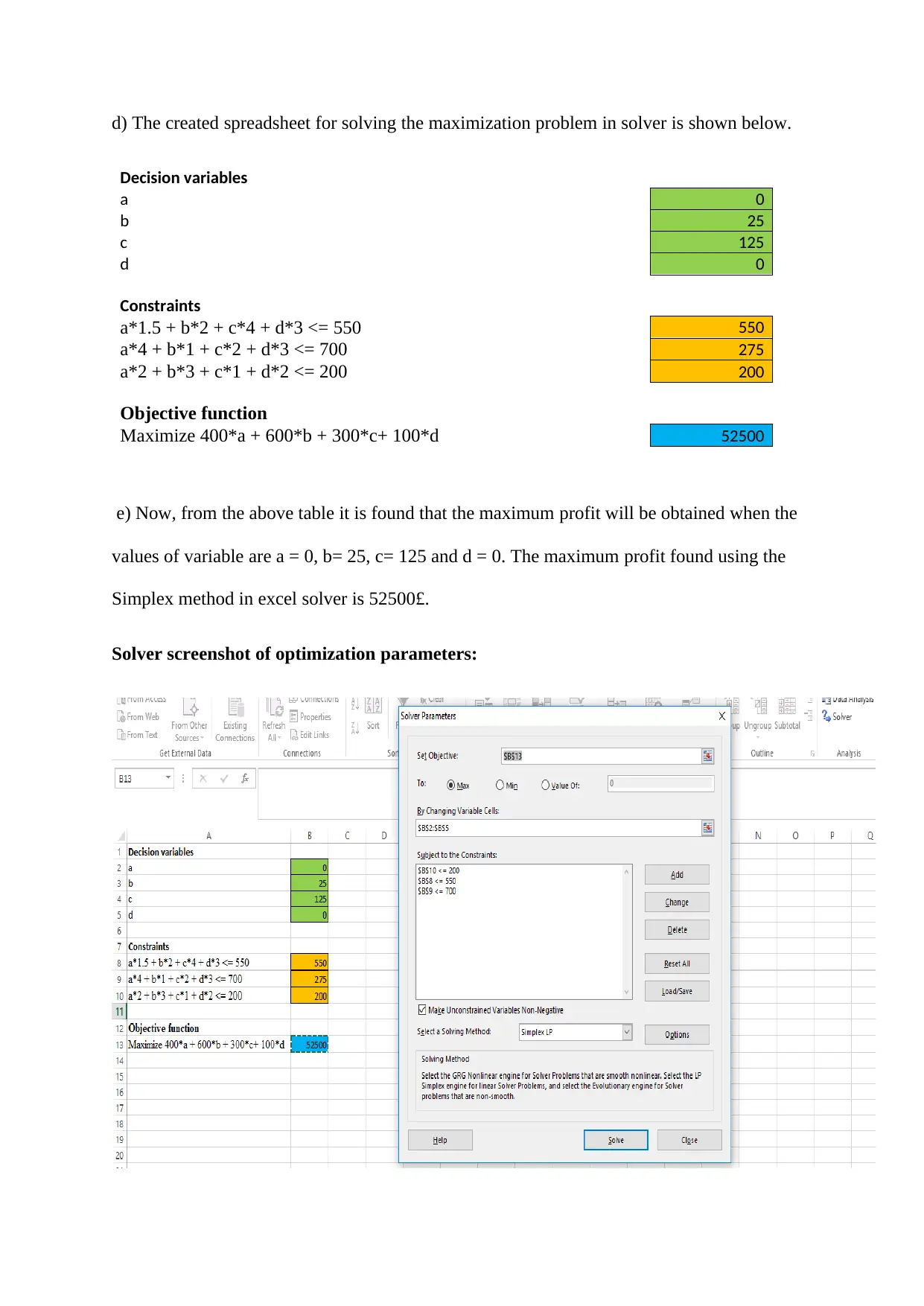
d) The created spreadsheet for solving the maximization problem in solver is shown below.
Decision variables
a 0
b 25
c 125
d 0
Constraints
a*1.5 + b*2 + c*4 + d*3 <= 550 550
a*4 + b*1 + c*2 + d*3 <= 700 275
a*2 + b*3 + c*1 + d*2 <= 200 200
Objective function
Maximize 400*a + 600*b + 300*c+ 100*d 52500
e) Now, from the above table it is found that the maximum profit will be obtained when the
values of variable are a = 0, b= 25, c= 125 and d = 0. The maximum profit found using the
Simplex method in excel solver is 52500£.
Solver screenshot of optimization parameters:

Hence, the number of fork lift models of W1,W2,W3 and W4 types for maximum profit are
0,25, 125 and 0 respectively.
Hence, it is recommended that for optimum profit of CAT company is 52500 £ if the types of
numbers of fork lift models produced are 0 W1 models, 25 W2 models, 125 W3 models and
0 W4 models respectively.
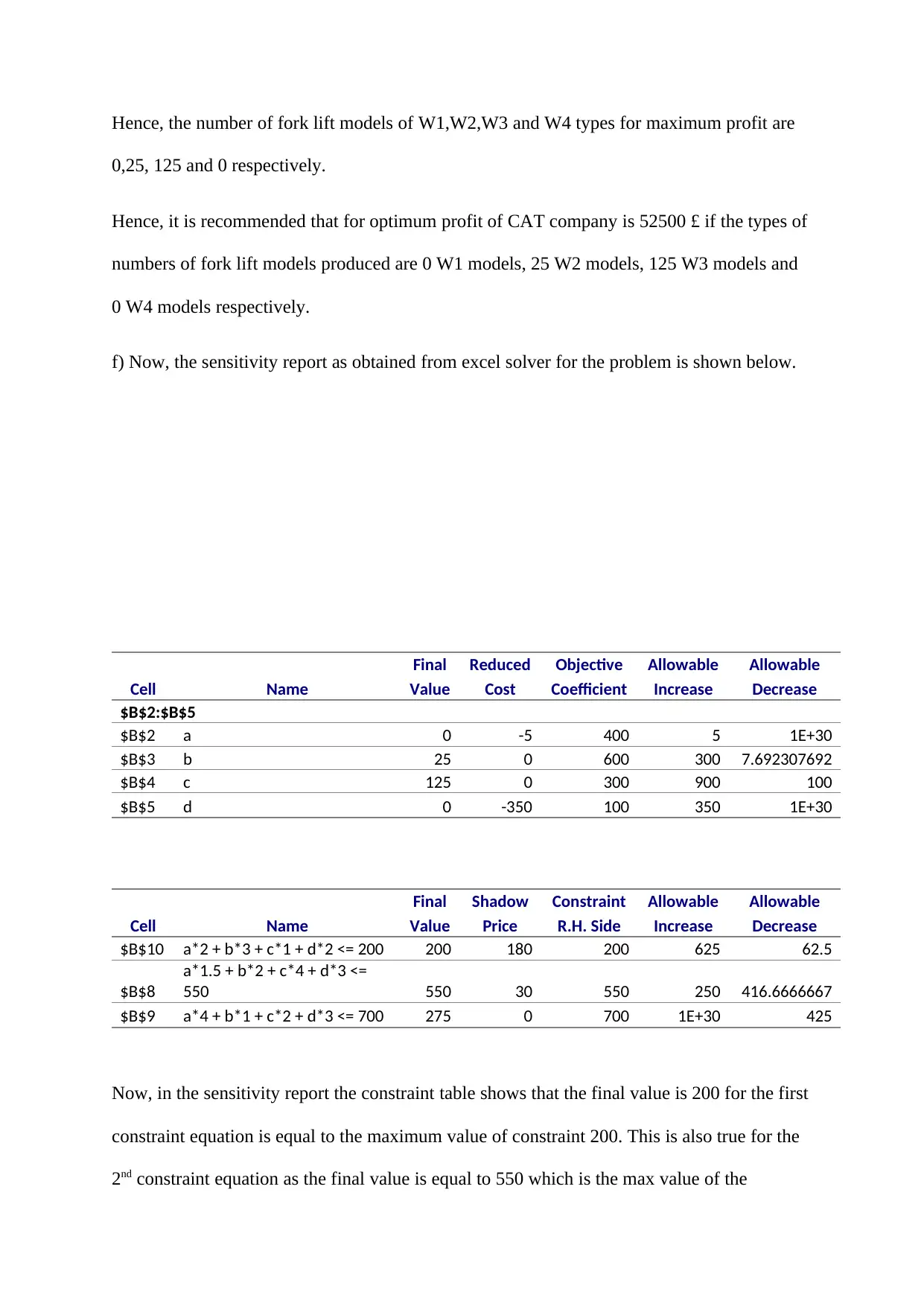
f) Now, the sensitivity report as obtained from excel solver for the problem is shown below.
Final Reduced Objective Allowable Allowable
Cell Name Value Cost Coefficient Increase Decrease
$B$2:$B$5
$B$2 a 0 -5 400 5 1E+30
$B$3 b 25 0 600 300 7.692307692
$B$4 c 125 0 300 900 100
$B$5 d 0 -350 100 350 1E+30
Final Shadow Constraint Allowable Allowable
Cell Name Value Price R.H. Side Increase Decrease
$B$10 a*2 + b*3 + c*1 + d*2 <= 200 200 180 200 625 62.5
$B$8
a*1.5 + b*2 + c*4 + d*3 <=
550 550 30 550 250 416.6666667
$B$9 a*4 + b*1 + c*2 + d*3 <= 700 275 0 700 1E+30 425
Now, in the sensitivity report the constraint table shows that the final value is 200 for the first
constraint equation is equal to the maximum value of constraint 200. This is also true for the
2nd constraint equation as the final value is equal to 550 which is the max value of the

constraint (Sanchez and Herrera 2016). Hence, these two constraints are the bottleneck for
this situation.
Additionally, from the sensitivity report it can be said that the profit from each unit of W2 is
600 £. From the allowable increase of 300 and allowable decrease of 7.69230769, it can be
said that the when the price of each unit of W2 is in between (600 - 7.692307692) = 592.3077
£ to 600 + 300 = 900 £ there will be no change in the optimum decision values i.e. a = 0, b=
25, c= 125 and d = 0 (Pentoś and Pieczarka 2017). This is similar for W1, W3 and W4 also.
From the constraints table when the 1st stage assembly hours is in between 200 – 62.5 = 137.5
hours to 200 + 625 = 825 hours the hours available in first stage will remain a binding
constraint or the slack will be zero (Proudlove 2017). The same is also true for stage 2 and
stage 3 of assembly also but the ranges of hours will be different as given the constraints
table.
g) Now, if another department can be set up by the CAT then it is best to set up the body
assembly department as this gives maximum limit of 700 hours in a month among the three
departments. This is because more numbers of units can be assembled when the hour limit in
a month is large which will maximize the profit even further.
h) The stage 3 decision can be impacted by the capacity issue in a large manner. The dataset
of actual processing time of the quality check and painting stage in different months over the
year 2017 is shown with respect to the fixed quality check and painting time in hours as given
the part e of the question.

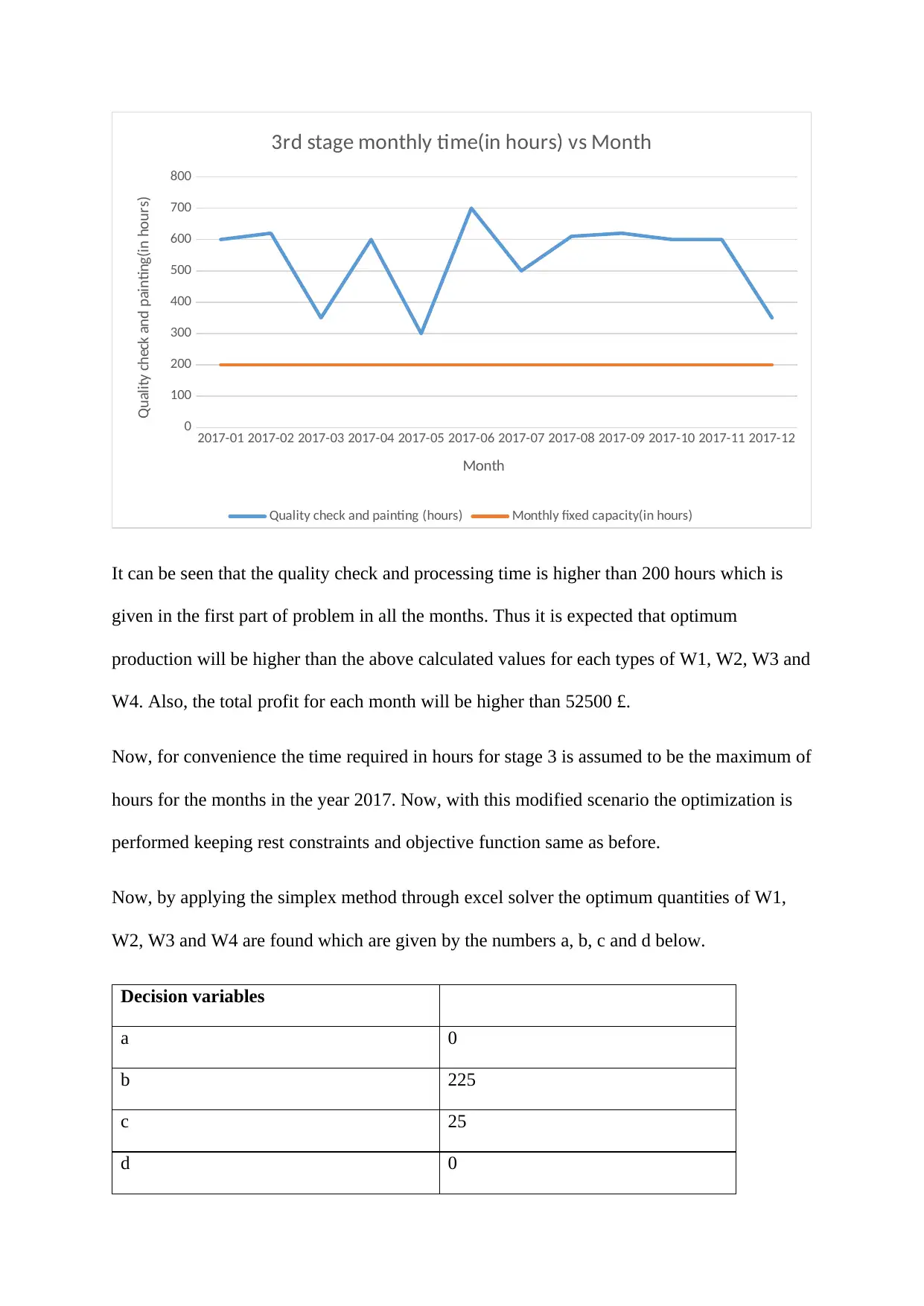
2017-01 2017-02 2017-03 2017-04 2017-05 2017-06 2017-07 2017-08 2017-09 2017-10 2017-11 2017-12
0
100
200
300
400
500
600
700
800
3rd stage monthly time(in hours) vs Month
Quality check and painting (hours) Monthly fixed capacity(in hours)
Month
Quality check and painting(in hours)
It can be seen that the quality check and processing time is higher than 200 hours which is
given in the first part of problem in all the months. Thus it is expected that optimum
production will be higher than the above calculated values for each types of W1, W2, W3 and
W4. Also, the total profit for each month will be higher than 52500 £.
Now, for convenience the time required in hours for stage 3 is assumed to be the maximum of
hours for the months in the year 2017. Now, with this modified scenario the optimization is
performed keeping rest constraints and objective function same as before.
Now, by applying the simplex method through excel solver the optimum quantities of W1,
W2, W3 and W4 are found which are given by the numbers a, b, c and d below.
Decision variables
a 0
b 225
c 25
d 0

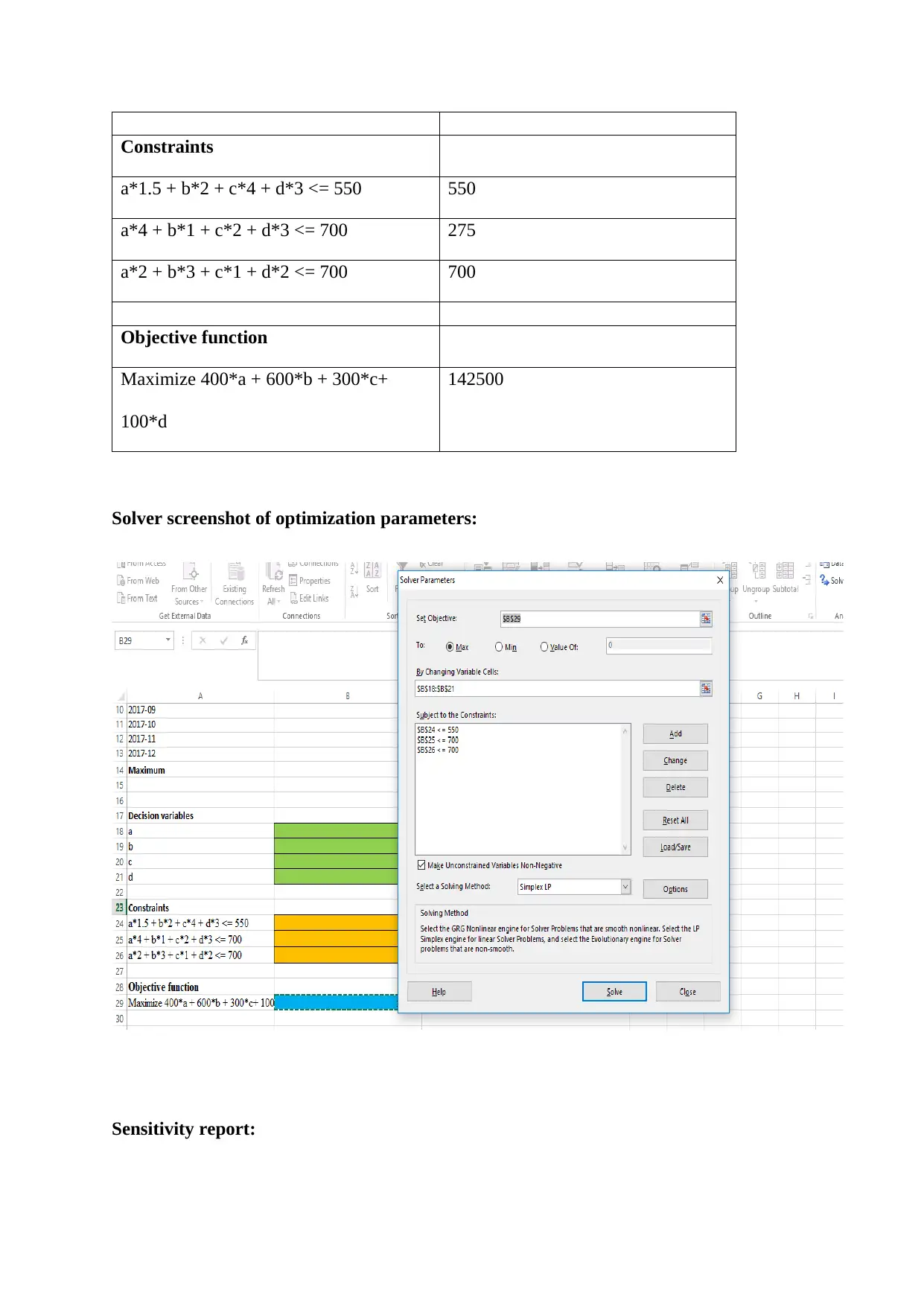
Constraints
a*1.5 + b*2 + c*4 + d*3 <= 550 550
a*4 + b*1 + c*2 + d*3 <= 700 275
a*2 + b*3 + c*1 + d*2 <= 700 700
Objective function
Maximize 400*a + 600*b + 300*c+
100*d
142500
Solver screenshot of optimization parameters:
Sensitivity report:

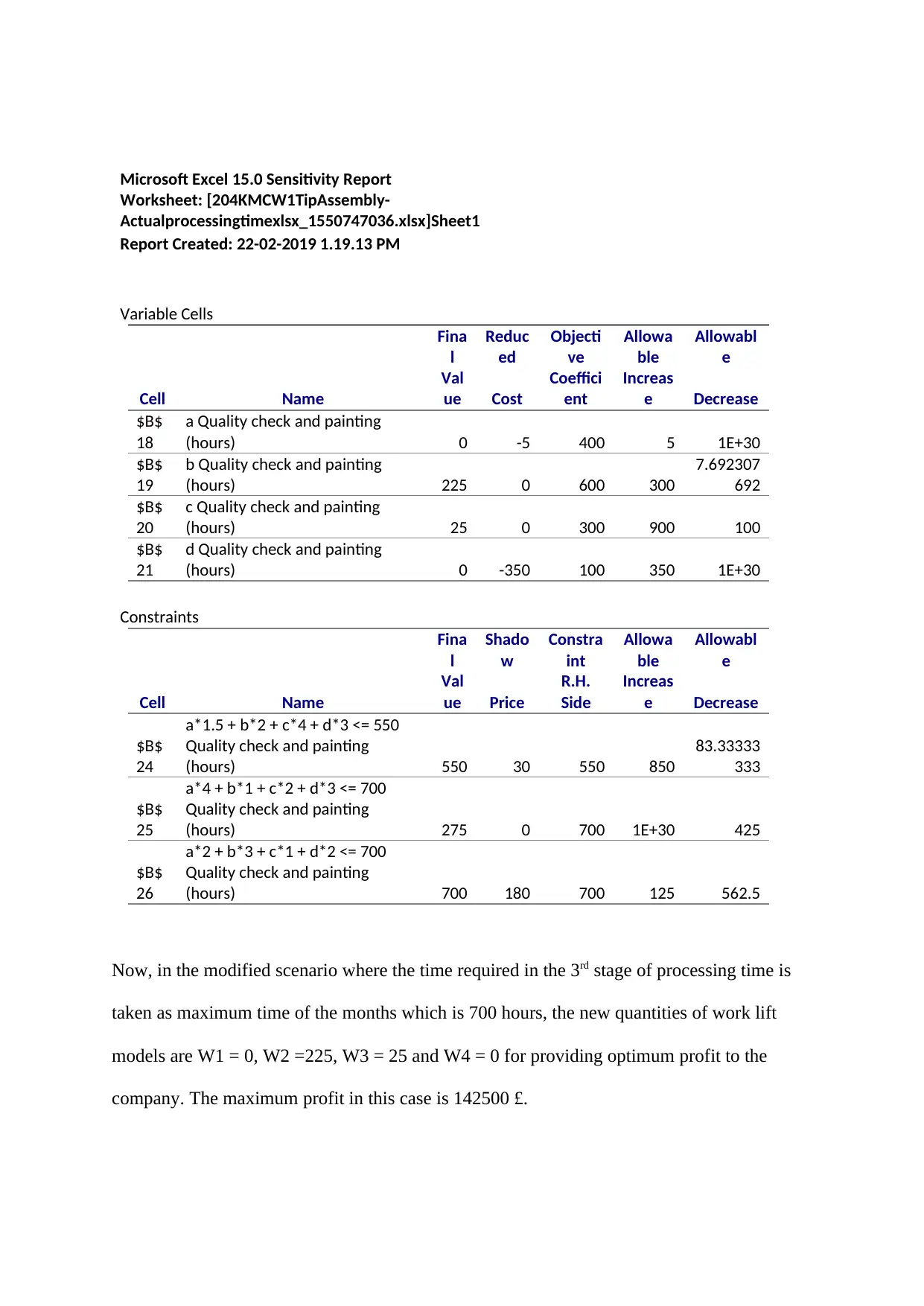
Microsoft Excel 15.0 Sensitivity Report
Worksheet: [204KMCW1TipAssembly-
Actualprocessingtimexlsx_1550747036.xlsx]Sheet1
Report Created: 22-02-2019 1.19.13 PM
Variable Cells
Fina
l
Reduc
ed
Objecti
ve
Allowa
ble
Allowabl
e
Cell Name
Val
ue Cost
Coeffici
ent
Increas
e Decrease
$B$
18
a Quality check and painting
(hours) 0 -5 400 5 1E+30
$B$
19
b Quality check and painting
(hours) 225 0 600 300
7.692307
692
$B$
20
c Quality check and painting
(hours) 25 0 300 900 100
$B$
21
d Quality check and painting
(hours) 0 -350 100 350 1E+30
Constraints
Fina
l
Shado
w
Constra
int
Allowa
ble
Allowabl
e
Cell Name
Val
ue Price
R.H.
Side
Increas
e Decrease
$B$
24
a*1.5 + b*2 + c*4 + d*3 <= 550
Quality check and painting
(hours) 550 30 550 850
83.33333
333
$B$
25
a*4 + b*1 + c*2 + d*3 <= 700
Quality check and painting
(hours) 275 0 700 1E+30 425
$B$
26
a*2 + b*3 + c*1 + d*2 <= 700
Quality check and painting
(hours) 700 180 700 125 562.5
Now, in the modified scenario where the time required in the 3rd stage of processing time is
taken as maximum time of the months which is 700 hours, the new quantities of work lift
models are W1 = 0, W2 =225, W3 = 25 and W4 = 0 for providing optimum profit to the
company. The maximum profit in this case is 142500 £.

The sensitivity table shows that when the profit by each W2 type is between the 592.3077
and 900 then the optimum values of the decision variables are unchanged. This also true for
other types W1, W3 and W4 but the ranges are different (Kaizzi et al. 2017). Also, from the
constraints table it is clear that when the time in hours in a month for stage 3 assembly
process is between 700 – 562.5 = 137.5 hours to 825 hours, the hours available in the stage 3
constraint will be a binding constraint or the slack will remain zero.

References:
Kaizzi, Kayuki C., Mohammed Beshir Mohammed, and Maman Nouri. "Fertilizer use
optimization: Principles and approach." Fertilizer use optimization in sub-Saharan Africa 17
(2017).
Pentoś, K. and Pieczarka, K., 2017. Applying an artificial neural network approach to the
analysis of tractive properties in changing soil conditions. Soil and Tillage Research, 165,
pp.113-120.
Proudlove, N., 2017. Using Excel for Basic Data Envelopment Analysis.
Sanchez, L.C. and Herrera, J., 2016. Solution to the multiple products transportation problem:
linear programming optimization with Excel Solver. IEEE Latin America Transactions,
14(2), pp.1018-1023.
Vanderbei, R.J., 2015. Linear programming. Heidelberg: Springer.