CHE 430: Unsteady State Material Balance and Process Control

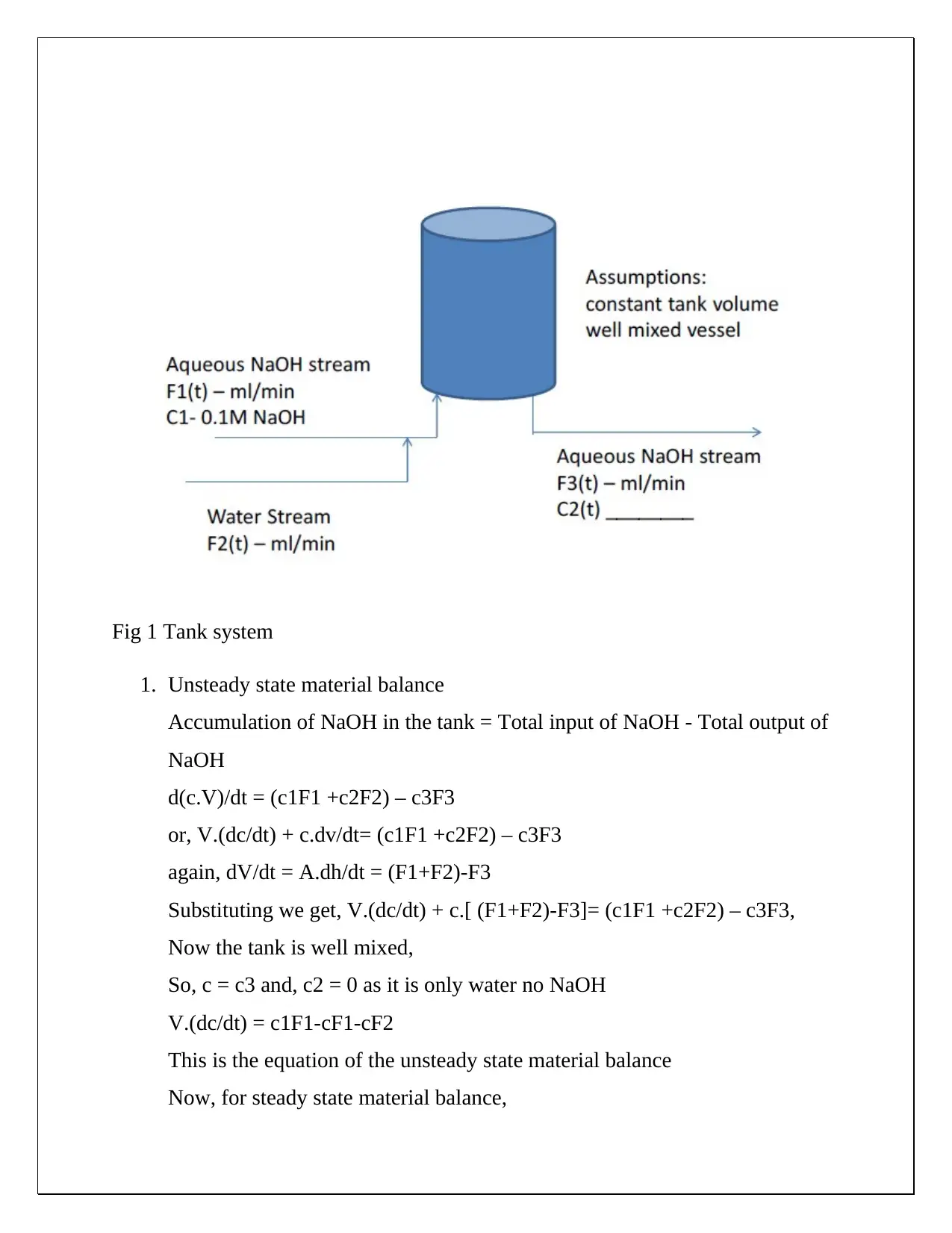
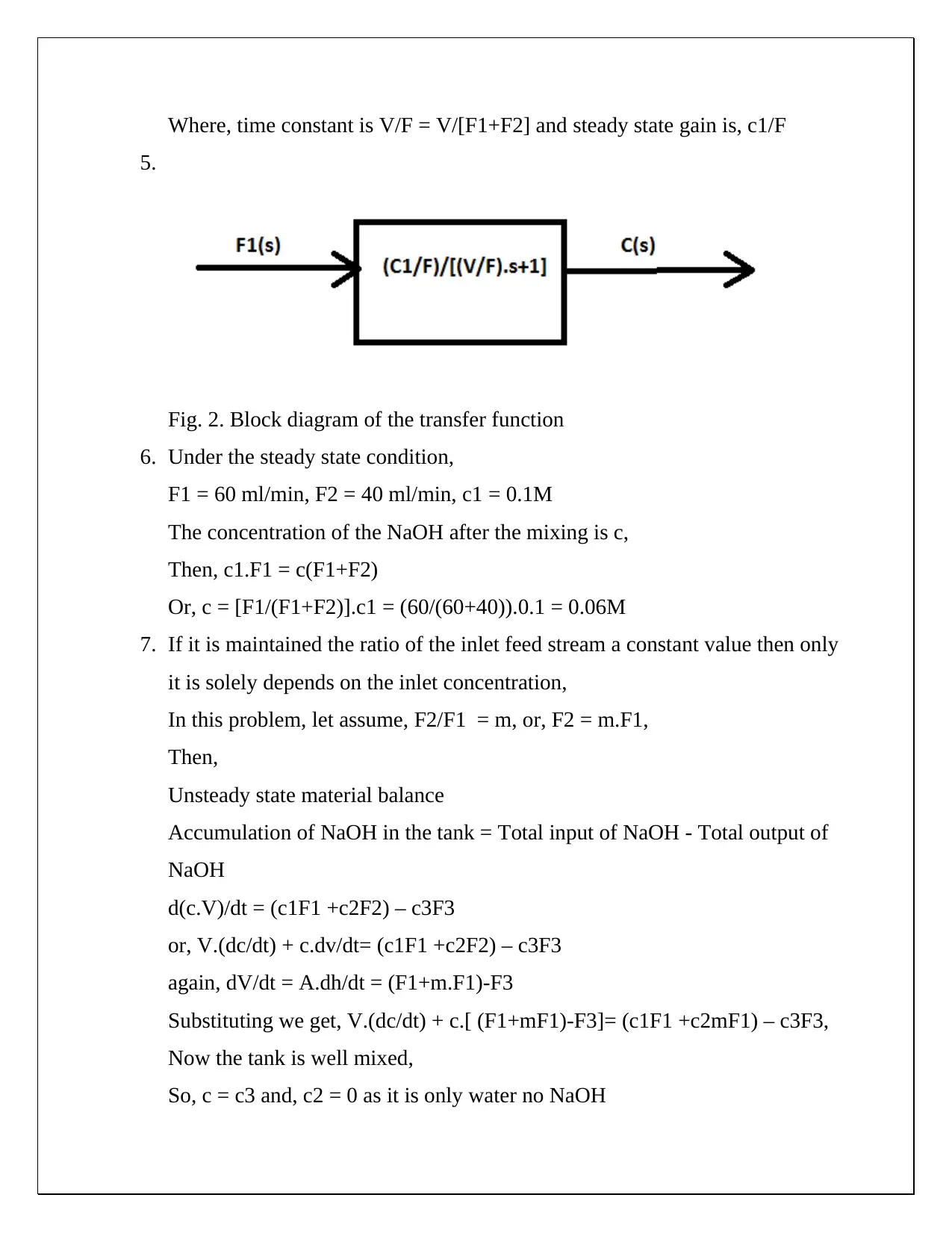
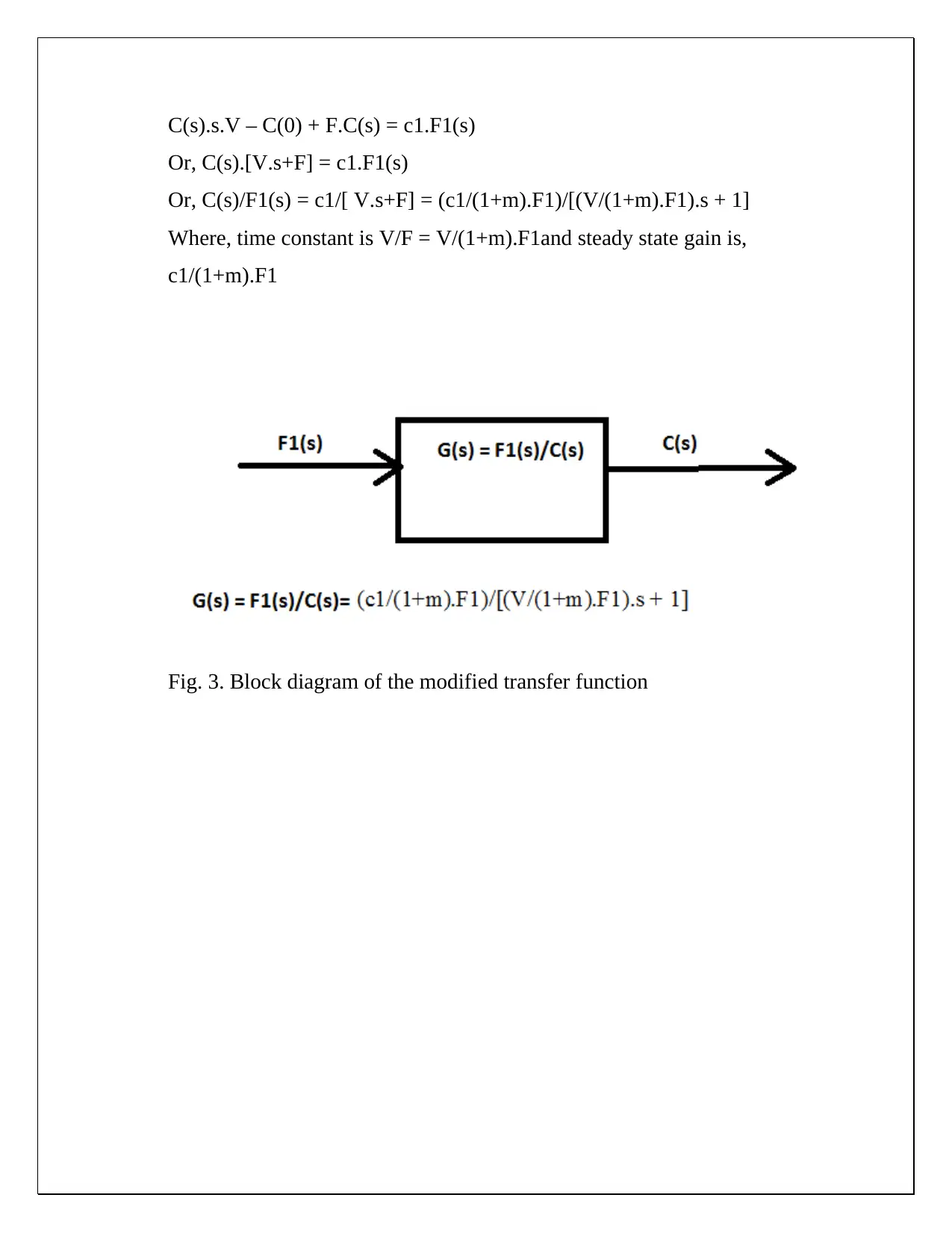
This document presents a comprehensive solution to a CHE 430 pre-lab assignment focused on unsteady state material balance. The solution begins by establishing unsteady and steady-state material balances for NaOH in a tank system, considering input and output flow rates. Non-linear terms are linearized, and deviation variables are defined to simplify the analysis. Laplace transforms are applied to derive transfer functions, steady-state gains, and time constants, allowing for the expression of outlet concentration in terms of flow disturbances. Block diagrams are created to visually represent the transfer functions. Furthermore, the solution calculates steady-state concentrations of NaOH at the mixing point and the mixer effluent under given flow rate and concentration conditions. The document also explores how to modify the process to ensure the outlet concentration depends solely on the inlet concentration. The solution provides detailed equations and calculations for both scenarios, including the derivation of modified transfer functions and block diagrams when the ratio of inlet feed streams is constant. The document demonstrates a strong understanding of chemical engineering principles related to process dynamics and control.

Fig 1 Tank system
1. Unsteady state material balance
Accumulation of NaOH in the tank = Total input of NaOH - Total output of
NaOH
d(c.V)/dt = (c1F1 +c2F2) – c3F3
or, V.(dc/dt) + c.dv/dt= (c1F1 +c2F2) – c3F3
again, dV/dt = A.dh/dt = (F1+F2)-F3
Substituting we get, V.(dc/dt) + c.[ (F1+F2)-F3]= (c1F1 +c2F2) – c3F3,
Now the tank is well mixed,
So, c = c3 and, c2 = 0 as it is only water no NaOH
V.(dc/dt) = c1F1-cF1-cF2
This is the equation of the unsteady state material balance
Now, for steady state material balance,

Accumulation of NaOH in the tank = Total input of NaOH - Total output of
NaOH
Here accumulation = 0
So, Total input of NaOH = Total output of NaOH
V.(dc/dt) = c1F1-cF1-cF2 = 0
Or, c1F1 = c(F1+F2)
2. Linearization of the equation,
V.(dc/dt) = c1F1-cF1-cF2
And, A.dh/dt = (F1+F2)-F3
Now, F3 = a.h where a is the constant
Then, A.dh/dt +a.h = (F1+F2)
3. Now, deviation variable, when t = 0, c3s = 0
There is no out flow as there is no concentration of the NaOH
Deviation variable, C3 = c3-c3s
Or, C3=c3
Again, H = h – hs
So, the equation reduces to,
V. dC/dt + C. (F1+F2) = C1F1
4. In the equation,
V. dC/dt + C. (F1+F2) = C1F1
Now, F1+F2 = F
So the equation reduces to,
V. dC/dt + C.F = C1F1
Taking the laplace transform of both side,
C(s).s.V – C(0) + F.C(s) = c1.F1(s)
Or, C(s).[V.s+F] = c1.F1(s)
Or, C(s)/F1(s) = c1/[ V.s+F] = (c1/F)/[(V/F).s + 1]

Where, time constant is V/F = V/[F1+F2] and steady state gain is, c1/F
5.
Fig. 2. Block diagram of the transfer function
6. Under the steady state condition,
F1 = 60 ml/min, F2 = 40 ml/min, c1 = 0.1M
The concentration of the NaOH after the mixing is c,
Then, c1.F1 = c(F1+F2)
Or, c = [F1/(F1+F2)].c1 = (60/(60+40)).0.1 = 0.06M
7. If it is maintained the ratio of the inlet feed stream a constant value then only
it is solely depends on the inlet concentration,
In this problem, let assume, F2/F1 = m, or, F2 = m.F1,
Then,
Unsteady state material balance
Accumulation of NaOH in the tank = Total input of NaOH - Total output of
NaOH
d(c.V)/dt = (c1F1 +c2F2) – c3F3
or, V.(dc/dt) + c.dv/dt= (c1F1 +c2F2) – c3F3
again, dV/dt = A.dh/dt = (F1+m.F1)-F3
Substituting we get, V.(dc/dt) + c.[ (F1+mF1)-F3]= (c1F1 +c2mF1) – c3F3,
Now the tank is well mixed,
So, c = c3 and, c2 = 0 as it is only water no NaOH

V.(dc/dt) = c1F1-cF1-c.mF1
This is the equation of the unsteady state material balance
Now, for steady state material balance,
Accumulation of NaOH in the tank = Total input of NaOH - Total output of
NaOH
Here accumulation = 0
So, Total input of NaOH = Total output of NaOH
V.(dc/dt) = c1F1-cF1-c mF1 = 0
Or, c1F1 = c(F1+ mF1)
Linearization of the equation,
V.(dc/dt) = c1F1-cF1-c mF1
And, A.dh/dt = (F1+ mF1)-F3
Now, F3 = a.h where a is the constant
Then, A.dh/dt +a.h = (F1+ mF1)
Now, deviation variable, when t = 0, c3s = 0
There is no out flow as there is no concentration of the NaOH
Deviation variable, C3 = c3-c3s
Or, C3=c3
Again, H = h – hs
So, the equation reduces to,
V. dC/dt + C. (F1+ mF1) = C1F1
In the equation,
V. dC/dt + C. (F1+ mF1) = C1F1
Now, F1+ mF1 = F
So the equation reduces to,
V. dC/dt + C.F = C1F1
Taking the laplace transform of both side,

C(s).s.V – C(0) + F.C(s) = c1.F1(s)
Or, C(s).[V.s+F] = c1.F1(s)
Or, C(s)/F1(s) = c1/[ V.s+F] = (c1/(1+m).F1)/[(V/(1+m).F1).s + 1]
Where, time constant is V/F = V/(1+m).F1and steady state gain is,
c1/(1+m).F1
Fig. 3. Block diagram of the modified transfer function