CITS5502 Software Processes: Analyzing and Modelling Code Production

This report focuses on modeling code production by analyzing data from students completing programming tasks in different languages. It involves fitting two models to three datasets, interpreting the model parameters, and answering questions related to software processes, specifically knowledge acquisition and encoding. The analysis includes calculating average times for tasks, curve fitting using Excel Solver to determine constants for each model, and comparing effort across different languages and problems through visualizations. The report concludes by identifying the most appropriate model based on minimum absolute error and discussing the impact of repeated attempts on coding efficiency, highlighting the importance of structured algorithm design in programming.

Running head: SOFTWARE PROCESS
SOFTWARE PROCESS
Name of the Student
Name of the University
Author Note

1SOFTWARE PROCESS
Introduction:
In this task the main objective is to perform task 1 and task 2 to have an insight about the
time needed to write problems in different languages when written repeatedly. In particular at
first 7 random students’ required time to write problem 1 in language A and B and problem 2
in language A is selected from a total of 14 students’ data. Then the average time is
calculated for each attempt for the three task and hence a total of 12 means are obtained.
Then two chosen models with respect to time(t) is fitted with each 4 set of effort(person-
minuites) data and the constants of the model is determined for which the model will
approximate the actual data. Additionally, some graphs about the comparison of effort for
different languages and different problems are drawn with respect to number of attempts to
compare the languages or problems.
1. Averaging data:
The time needed to do the task P1LA, P2LA and P1LB in four attempts at an interval 3
days by the 14 students are given below.
Tim
e 0 1 2 3 0 1 2 3 0 1 2 3
Problem 1 Language A
Problem 2
Language A
Problem 1 Language
B
1
17
5 140
21
1 73
20
8
15
4
14
4
12
8
13
7
11
1
11
3 101
2
37
0 110 30 25
28
6 53 36 27
10
0 44 32 13
3
27
0 170
11
7
11
4 50 59 45 40
10
5 80 60 60
4 80 35 16 13 78 42 39 19
11
3 50 29 29
5 80 23 30 13 59 33 20 13
13
9 63 28 22
6 55 20 19 18 83 15 13 13
11
5 35 29 41
7
12
7 46 50 56 97 46 67 39
11
5 50 56 52
8 26 70 63 21 10 42 44 31 14 97 92 58

2SOFTWARE PROCESS
5 3 6
9
20
5 165 58 64
15
0
11
5
10
7
10
2
15
9
11
3 87 82
10 52 18 71 21 34 17 18 16 17 15 21 14
11
21
0 71 63 26 60 31 21 18 38 32 71 24
12
16
9 82 47 27 73 38 91 58
10
6 22 28 28
13
21
2 253 54 47 46 34 25 17 73 32 26 19
14
15
0 75 63 45 75 78 27 26 73
13
5 28 66
In this task 7 out of 14 students are selected at random in excel by using the excel
function (choose(randbetween(1,14),time 1, time 2,…time 14). Now, after generating the
time needed of a randomly chosen 7 students, the values are pasted to stop them from
updating. The generated times and the average is shown below.
Selected(0) Selected(1) Selected(2) Selected(3) Selected(0) Selected(1) Selected(2) Selected(3)Selected(0) Selected(1) Selected(2) Selected(3)
127 46 117 25 75 38 144 102 146 80 32 41
80 165 211 27 73 15 39 128 115 32 87 82
169 165 50 47 59 42 18 13 17 35 29 101
169 75 54 64 97 42 44 58 38 35 29 29
55 71 63 27 208 78 107 26 73 44 28 29
150 165 63 45 78 31 13 13 106 97 28 29
55 35 71 25 103 78 44 31 100 97 28 24
115 103.142857 89.8571429 37.1428571 99 46.2857143 58.4285714 53 85 60 37.2857143 47.8571429
Problem 2 Language A Problem 1 Language BProblem 1 Language A
The average times of 7 students in each attempt of solving three tasks are shown in bold
at the bottom row.
2. Curve Fitting:

3SOFTWARE PROCESS
Now, in this task two models are chosen to fit the effort from each attempt with respect to
the time. Hence, each attempt has 4 data points which are fitted with the effort calculated
from models.
The chosen models are
1) Model M2= Effort = (a+bct)/(bt+1)
2) Model M4 = Effort = (a-c)(t+1)^(-b) + c
Now, the error for fitting is estimated by calculating the absolute value of model effort
and the obtained effort from the average time needed for 7 students (Wang et al. 2016).
3. Report
The values of a,b and c are calculated by using the excel solver in which the objective
function is the total error which is to minimized by varying the constants a,b and c
subjected to constraints a, b and c are greater than zero (Winston 2016).
P1LA M2 effort table:
Time Effort
Effort
(From
Model)
Error
0 115 141.032646 26.03265
1 103.1429 75.2949115 27.84795
2 89.85714 52.536914 37.32023
3 37.14286 40.9924855 3.849628
95.05045TOTAL
The a,b,c constants are
a b c
141.03264
6
0.944278 5.677957

4SOFTWARE PROCESS
0 0.5 1 1.5 2 2.5 3 3.5
0
20
40
60
80
100
120
140
160
Actual and model effort
Effort Model 1
Attempt
Effort (mins)
P2LA M2 effort table:
Time Effort Effort
(from Model) Error
0 99 84 15
1 46.285714 51 4.714286
2 58.428571 46.28571429 12.14286
3 53 44.4 8.6
40.45714TOTAL
a b c
84 3 40
0 0.5 1 1.5 2 2.5 3 3.5
0
10
20
30
40
50
60
70
80
90
Actual and model effort
Effort Model 1
Attempt
Effort (mins)

5SOFTWARE PROCESS
P1LB M2 Effort table:
Time Effort
Effort
(from
Model)
Error
0 85 121.7354 36.73536
1 60 58.0527 1.947296
2 37.28571 47.66421 10.3785
3 47.85714 43.40488 4.452259
53.51341Total
a b c
121.7354 2.565057 33.22571
0 0.5 1 1.5 2 2.5 3 3.5
0
20
40
60
80
100
120
140
Actual and model
effort
Effort Model 1
Attempts
Effort (mins)
P1LA M4 effort table:
Time Effort
Effort
(from
Model)
Error
0 115 140.8939 25.89393
1 103.1429 75.65247 27.49039
2 89.85714 52.62031 37.23684
3 37.14286 40.69043 3.547576
94.16873Total
a b c
140.8939 0.9 0.321645

6SOFTWARE PROCESS
0 0.5 1 1.5 2 2.5 3 3.5
0
20
40
60
80
100
120
140
160
Actual and model
eff ort
Effort Model 2
Attempts
Effort (mins)
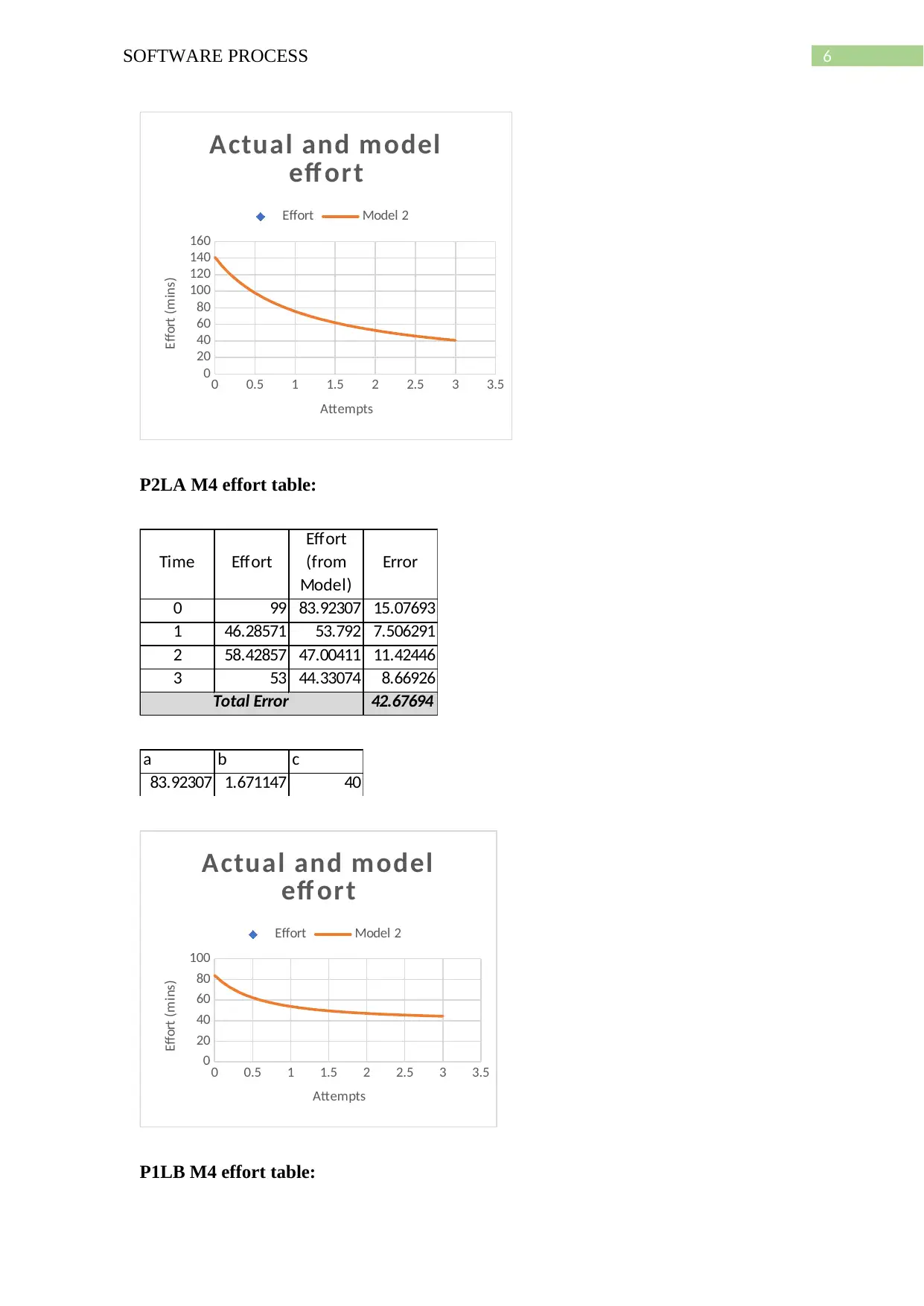
P2LA M4 effort table:
Time Effort
Effort
(from
Model)
Error
0 99 83.92307 15.07693
1 46.28571 53.792 7.506291
2 58.42857 47.00411 11.42446
3 53 44.33074 8.66926
42.67694Total Error
a b c
83.92307 1.671147 40
0 0.5 1 1.5 2 2.5 3 3.5
0
20
40
60
80
100
Actual and model
eff ort
Effort Model 2
Attempts
Effort (mins)
P1LB M4 effort table:

7SOFTWARE PROCESS
Time Effort
Effort
(from
Model)
Error
0 85 120 35
1 60 58.63548 1.364523
2 37.28571 47.27168 9.985962
3 47.85714 43.29435 4.562797
50.91328TOTAL
a b c
120 2 38.18064
0 0.5 1 1.5 2 2.5 3 3.5
0
20
40
60
80
100
120
140
Actual and model
eff ort
Effort Model 1
Attempts
Effort (mins)
The most appropriate model to represent the actual values of required time is model with
minimum absolute error. Hence, from the above graphs it can be seen that the model M2
when fitted for the time data of solving problem 2 by language A produces the least
absolute error of 40.46. Hence, model M2(effort = (a+bct)/(bt+1)) is the most appropriate
model.
Hence, the minimum time that can be taken to solve any of the three problems is
approximately 37 mins as this is lowest time required in the above tables.
Now, the effort in mins to write program 1 is compared for two different language A and
B with respect to the attempts by the following graph.

8SOFTWARE PROCESS
0 0.5 1 1.5 2 2.5 3 3.5
0
20
40
60
80
100
120
140
Program 1
Language A Language B
Attempts
Effort (mins)
Hence, it is clear the writing program 1 in language B is easier as the effort in mins is less
in this case.
Again, the efforts(mins) w.r.t number of attempts is compared for writing program 1 and
program 2 in language A and for different language with different problems (problem 1
and problem 2).

9SOFTWARE PROCESS
0 0.5 1 1.5 2 2.5 3 3.5
0
20
40
60
80
100
120
140
160
Model 2
P1LA P2LA
Attempts
Efforts (mins)
0 0.5 1 1.5 2 2.5 3 3.5
0
20
40
60
80
100
120
140
160
Model 4
P1LA P2LA
Attempts
Efforts (mins)
Hence, from the above two graphs it is clear that both of the model approximately
predicts the same effort for writing problem 1 in different languages.

10SOFTWARE PROCESS
Conclusion:
Hence, the objectives of this experiment have been successfully met as the average
time calculation from randomly selected times and curve fitting with the help of excel
solver is performed with least errors and the visualizations through different graphs are
obtained which clearly shows the comparison between the problems, languages and the
trend of effort time with respect to attempts. As the minimum errors in some model are
quite large when fitted with some of the Effort data, some other models can be selected
from four models or a custom model can be created to minimize the absolute errors. The
above graphs also show that when writing the same problem in consecutively in the same
language the time needed to write the codes is reduced and this is true for writing in some
other language also. Hence, this proves that when the algorithm to solve a particular
problem is created then it becomes easier to write in any languages. Hence, creating the
proper, structured algorithm for the problem is the essential part of programming.

11SOFTWARE PROCESS
References:
Wang, B., Zhou, S., Liu, W. and Mo, Y., 2015. Indoor Localization Based on Curve
Fitting and Location Search Using Received Signal Strength. IEEE Trans. Industrial
Electronics, 62(1), pp.572-582.
Winston, W., 2016. Microsoft Excel data analysis and business modeling. Microsoft
press.