CMPE 263: Digital Logic Circuit and Data Representation Homework 1

This document presents a comprehensive solution to Homework 1 for the Computer Architecture and Organization I course (CMPE 263) at Qatar University. The assignment covers fundamental concepts in digital logic and data representation. Solutions include simplified Boolean functions using Karnaugh maps and logic diagrams using AND-OR and NAND gates. The document also addresses JK flip-flop conversion, priority encoder design, sequential circuit analysis, and multiplexer construction. Furthermore, it provides detailed explanations and solutions for binary and decimal number conversions, including unsigned and signed representations using 2's complement arithmetic. The assignment concludes with solutions for error detection using odd parity generators and checkers. This document is a valuable resource for students studying computer architecture and digital logic, offering detailed explanations and step-by-step solutions to aid in understanding the core concepts.

Student ID:Name:
Computer Architecture and
Organization I
CMPE 263
Spring 2018
March 2018
Dept. of Computer Science and
Engineering
College of Engineering
Qatar University
Homework #1 – Spring 2018
Digital Logic Circuit and Data Representation
Question #1 (4 marks):
Given the Boolean function:
F ( A , B , C , D)=∑ m(0,2,3,5,7,8,10,11,13,15)
1) [2 marks] Drive the simplified Boolean function in sum-of-products form by
means of a four-variable Karnaugh map.
2) Draw the logic diagram with
a. [1 mark] AND-OR gates;
b. [1 mark] NAND gates.
Solution:
Page 1 of 12
50

Student ID:Name:
Question #2 (2 marks):
Given a JK flip flop, show how can you convert it into a D flip-flop.
Page 2 of 12

Student ID:Name:
Question #3 (6 mark):
Design a priority encoder with three inputs X, Y, Z and three outputs A, B, C. The
truth table for the circuit is shown below.
a) [3 marks] Drive the minimized logic equations for A, B, and C (use Karnaugh
maps).
b) [3 marks] Draw the logic circuit diagram for A, B, and C.
X Y ZA B C
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0 0 0
0 0 1
0 1 1
0 1 1
1 0 1
1 0 1
1 0 1
1 0 1
Page 3 of 12

Student ID:Name:
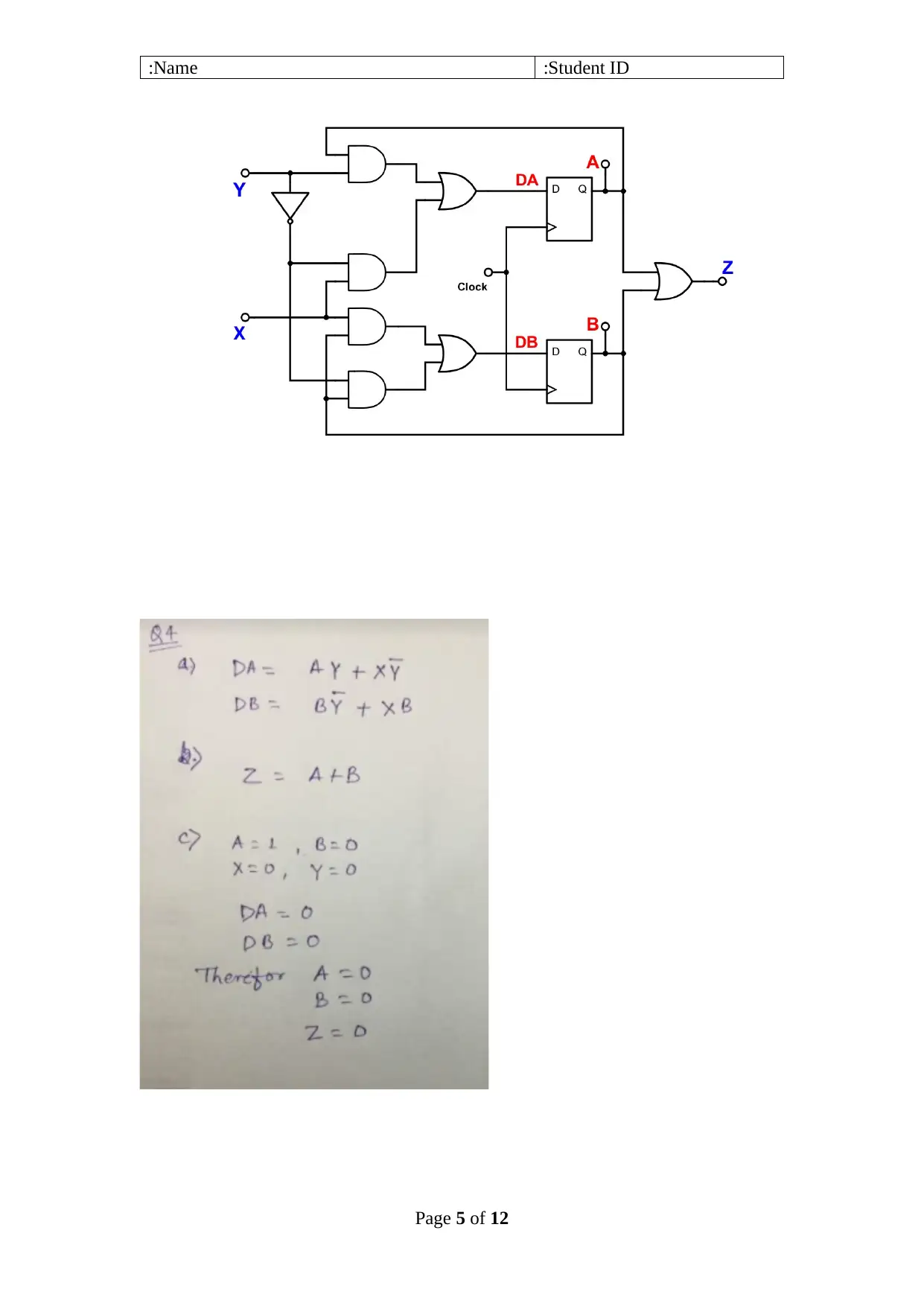
Question #4 (6 mark):
Given a sequential circuit (shown in the figure below) that has two D flip-flops A and
B, two inputs X and Y, and one output Z.
a) [2 marks] Write the logic function for the flip-flops inputs DA and DB, as a
function of X, Y, A and B.
b) [1 mark] Write the logic function for the output Z.
c) [3 marks] If the present state of A and B are A = 1 and B = 0, and the circuit
inputs are X = 0 and Y = 0.
Then, what will be the next state values for the flip-flops A and B?
What will be the value of output Z, in this case?
Page 4 of 12

Student ID:Name:
Page 5 of 12

Student ID:Name:
Question #5 (3 marks):
The content of a 4-bit register is initially 1011. The register is shifted six times to the
right, with the serial input (SI) being 110011. What is the content of the register after
each shift? (Fill the table below.)
Q3 Q2 Q1 Q0
Initial content of register1 0 1 1
Content after first shift1 1 0 1
Content after second shift1 1 1 0
Content after third shift0 1 1 1
Content after fourth shift1 0 1 1
Content after fifth shift1 1 0 1
Content after sixth shift1 1 1 0
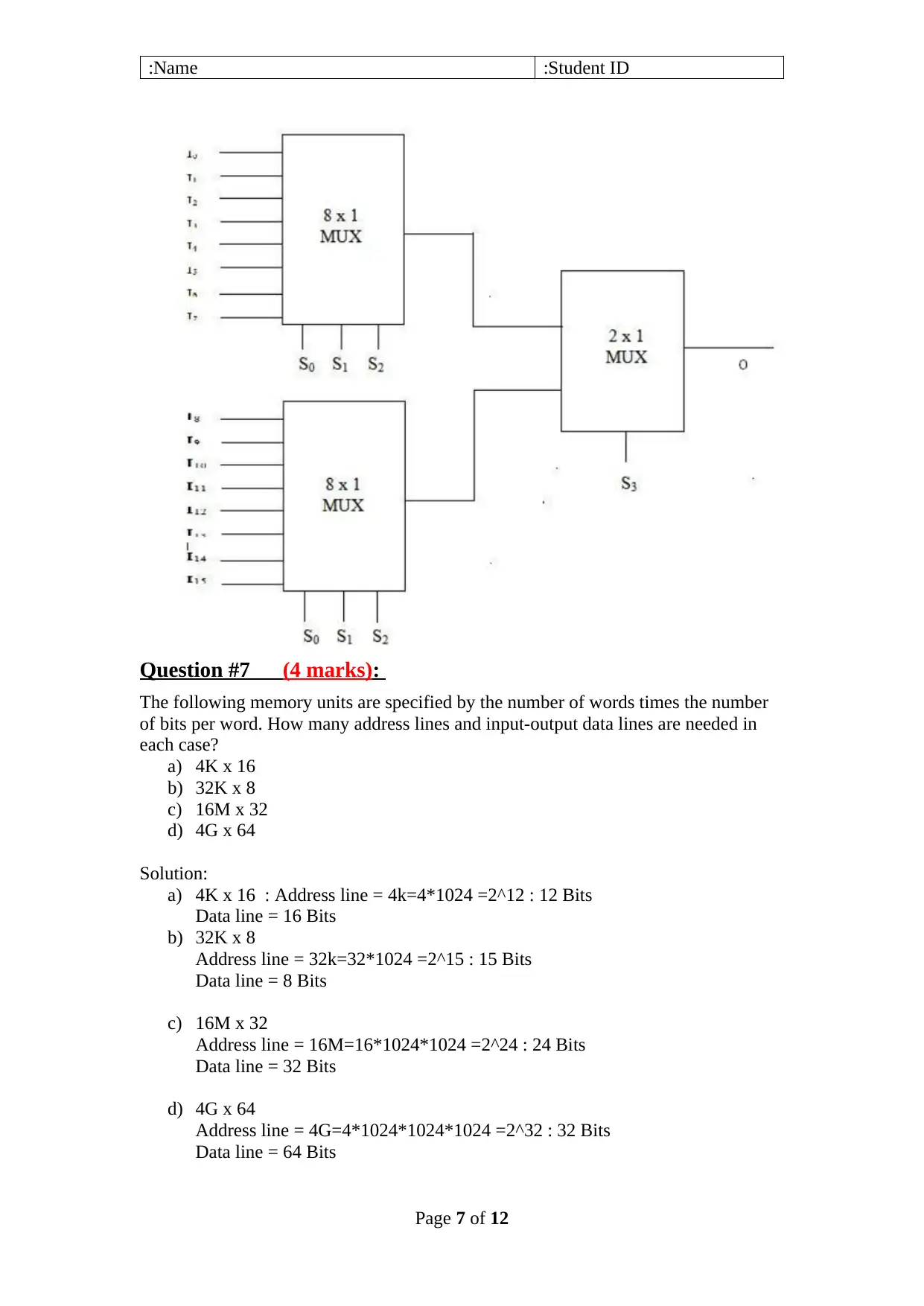
Question #6 (3 marks):
Construct a 16-to-1 line multiplexer with two 8-to-1 line multiplexers and one 2-to-1
line multiplexer. Use block diagrams for the three multiplexers.
Solution: Multiplexer is one of the basic building units of a computer system which in
principle allows sharing of a common line by more than one input lines. It connects
multiple input lines to a single output line. At a specific time one of the input lines is
selected and the selected input is passed on to the output line.
Page 6 of 12

Student ID:Name:
Question #7 (4 marks):
The following memory units are specified by the number of words times the number
of bits per word. How many address lines and input-output data lines are needed in
each case?
a) 4K x 16
b) 32K x 8
c) 16M x 32
d) 4G x 64
Solution:
a) 4K x 16 : Address line = 4k=4*1024 =2^12 : 12 Bits
Data line = 16 Bits
b) 32K x 8
Address line = 32k=32*1024 =2^15 : 15 Bits
Data line = 8 Bits
c) 16M x 32
Address line = 16M=16*1024*1024 =2^24 : 24 Bits
Data line = 32 Bits
d) 4G x 64
Address line = 4G=4*1024*1024*1024 =2^32 : 32 Bits
Data line = 64 Bits
Page 7 of 12

Student ID:Name:
Question #8 (3 marks):
Convert the following (unsigned) binary numbers to decimal. (Note that the numbers
have a fractional part):
a) 101110.1
b) 101010.01
c) 100111.101
Solution
a) 101110.1
( 101110 )2 = ( 46 )10
Explanation
Step 1:
Start at the rightmost digit. Take that digit and multiply with 20 (20 = 1). Multiple second
digit with 21, third with 22...
In this example we have:
0 * 20 = 0 * 1 = 0
1 * 21 = 1 * 2 = 2
1 * 22 = 1 * 4 = 4
1 * 23 = 1 * 8 = 8
0 * 24 = 0 * 16 = 0
1 * 25 = 1 * 32 = 32
Step 2:
Add together all products
0 + 2 + 4 + 8 + 0 + 32 = 46
Smilarly the Fractional part of Number will be converted to decimal by division by
2
( 101110.1 )2 = ( 46.5 )10
b) 101010.01
( 101010 )2 = ( 42 )10
Explanation
Step 1:
Start at the rightmost digit. Take that digit and multiply with 20 (20 = 1). Multiple second
digit with 21, third with 22...
In this example we have:
0 * 20 = 0 * 1 = 0
1 * 21 = 1 * 2 = 2
0 * 22 = 0 * 4 = 0
1 * 23 = 1 * 8 = 8
0 * 24 = 0 * 16 = 0
1 * 25 = 1 * 32 = 32
Step 2:
Add together all products
0 + 2 + 0 + 8 + 0 + 32 = 42
Similarly .01 = 0/2 + ¼=0.25
( 101010.01 )2 = ( 42.25 )10
c) 100111.101
( 100111 )2 = ( 39 )10
Page 8 of 12

Student ID:Name:
Explanation
Step 1:
Start at the rightmost digit. Take that digit and multiply with 20 (20 = 1). Multiple second
digit with 21, third with 22...
In this example we have:
1 * 20 = 1 * 1 = 1
1 * 21 = 1 * 2 = 2
1 * 22 = 1 * 4 = 4
0 * 23 = 0 * 8 = 0
0 * 24 = 0 * 16 = 0
1 * 25 = 1 * 32 = 32
Step 2:
Add together all products
1 + 2 + 4 + 0 + 0 + 32 = 39
Similarly .101 = ½+0/4+1/8=0.625
( 100111.101 )2 = ( 39.625 )10
Question #9 (4 marks) :
Convert the following decimal numbers to binary: 133.375. Show the steps of your
work.
Solution:
The integral part of the decimal number is converted to binary by successive division
by 2
Therefore 133 will be successively divided by 2
( 133 )10 = ( 10000101 )2
Explanation
Step 1:
Write down the decimal number and continually divide by 2 to give a result and a
remainder. The remainder is either a 1 or a 0.
In this example we have:
133 / 2 result 66 remainder 1
66 / 2 result 33 remainder 0
33 / 2 result 16 remainder 1
16 / 2 result 8 remainder 0
8 / 2 result 4 remainder 0
4 / 2 result 2 remainder 0
2 / 2 result 1 remainder 0
1 / 2 result 0 remainder 1
Step 2:
Read the remainders from bottom to top.
Similarly Fractional part will be converted to binary by successive multiplication by 2
0.375*2=0.75 Take 0
0.75*2=1.5 Take 1
0.5*2=1 Take 1
Therefore
( 133.375 )10 = ( 10000101.011 )2
Question #10 (3 marks) :
Page 9 of 12

Student ID:Name:
Convert the BCD (base 16) number FA35D1 to binary (base 2) and octal (base 8).
Show the steps of your work.
Solution:
Given Number = FA35D1
We can convert this to Binary by writing binary equivalent of each digit in a bunch of
4 bits
FA35D1 = 111110100011010111010001
Binary to octal conversion is easy and we can do that by grouping 3 bits for each digit
111110100011010111010001 = 111 110 100 011 010 111 010 001=(76432721)o
Question #11 (8 marks) :
Add the following numbers in binary using 2’s complement to represent negative
numbers. Use word length of 6 bits (including sign bit), and show if overflow occurs.
a) 12 + (-5)
b) (-12) + 11
c) 22 + 11
d) (-11) + (-21)
Solution:
Page 10 of 12

Student ID:Name:
Question #12 (4 marks) :
For error detection in a 3-bit data (XYZ):
a) Design an odd parity generator
Page 11 of 12

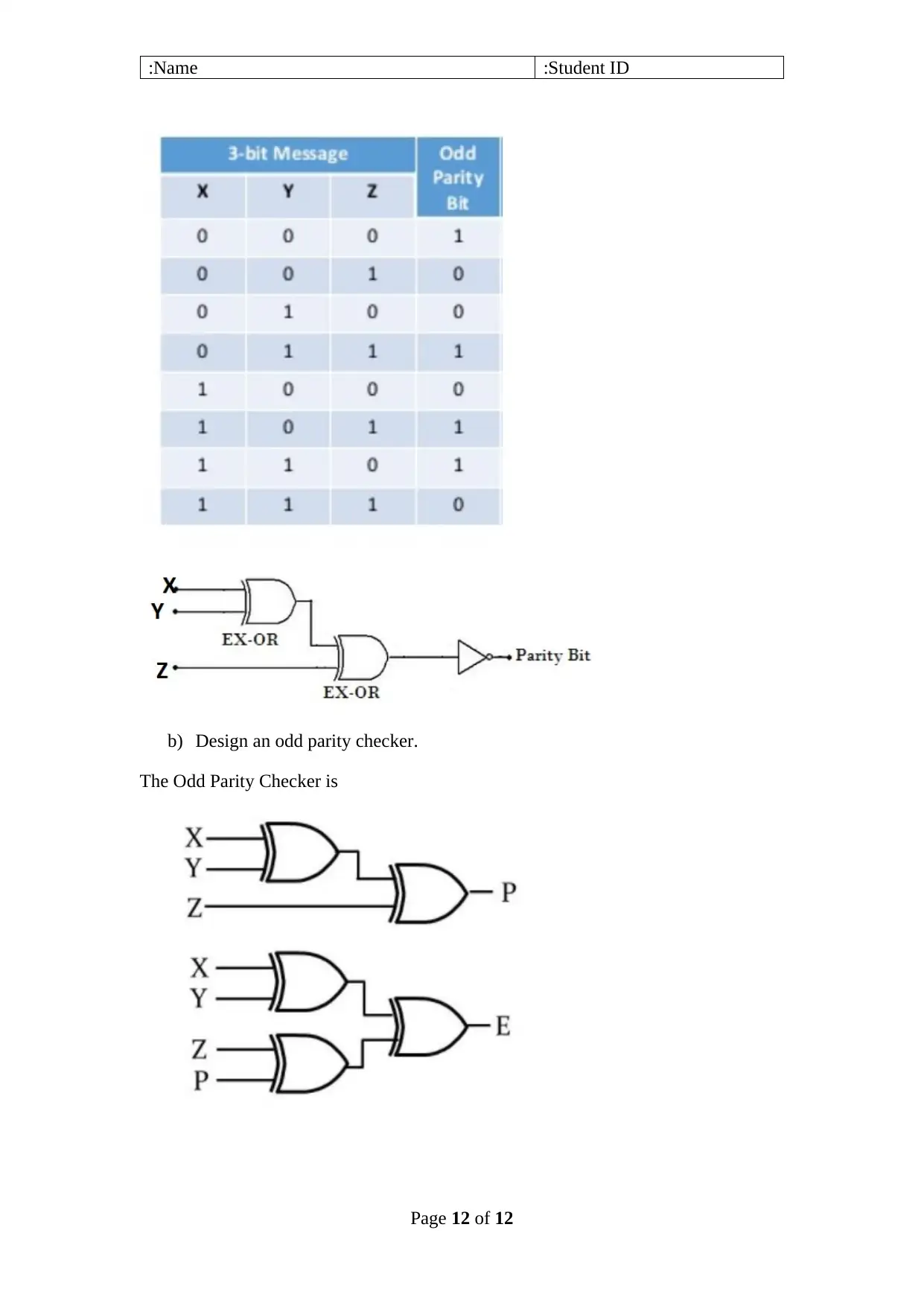
Student ID:Name:
b) Design an odd parity checker.
The Odd Parity Checker is
Page 12 of 12