2018 Griffith University Coastal Engineering Assignment: Simple Models
VerifiedAdded on 2023/06/10
|13
|2158
|360
Project
AI Summary
This assignment addresses two key aspects of coastal engineering. Question 1 focuses on developing a model to estimate swell wave height at the coast using data from a submerged pressure sensor and calculating the shoaling coefficient for five storm events. The analysis utilizes MATLAB to process wave characteristics like wave height, wavelength, and wave celerity, and includes graphical illustrations of relative water depth and shoaling coefficients. Question 2 involves analyzing sediment transport rates and shoreline changes between 1993 and 2015. A numerical model is developed using MATLAB to simulate shoreline positions, incorporating data from sediment transport and aerial views. The model calculates the root mean square error (RMSE) and plots sediment and shoreline trends, offering insights into coastal erosion and sediment dynamics. The report concludes with a discussion of the MATLAB software's efficiency in coastal engineering modeling.

2018
GRIFFITH UNIVERSITY
COASTAL ENGINEERING AND MODELLING-6110 ENG
TRIMESTER 1, 2018
TITLE: SIMPLE COASTAL MODELS
ASSIGNMENT 1
STUDENT NAME
STUDENT ID NUMBER
PROFESSOR (TUTOR)
DATE OF SUBMISSION
GRIFFITH UNIVERSITY
COASTAL ENGINEERING AND MODELLING-6110 ENG
TRIMESTER 1, 2018
TITLE: SIMPLE COASTAL MODELS
ASSIGNMENT 1
STUDENT NAME
STUDENT ID NUMBER
PROFESSOR (TUTOR)
DATE OF SUBMISSION
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

QUESTION 1
INTRODUCTION
Basic overview
Ocean waves are formed when the energy moves through a medium it is termed to be a
progressive wave. Progressive waves arise from forces that transmit energy through the water
columns or on the surface. Waves classification is based on the attributes namely period,
wavelength, frequency and distributing forces. Ocean swells are the long wavelength surface
wave groups with tend to travel long distances and are more stable than the wind waves. The
swells move from different parts of the ocean to the shoreline.
Problem statement
For analysis purposes, a submerged pressure sensor can be used as a wave gauge. It is
implemented to detect the wave induced dynamic pressure. In the analysis, a swell wave that has
deep water attributes propagates orthogonally towards a straight shoreline. During the analysis,
data was collected from about 5 storm events. There is need to develop a model to estimate the
swell wave height at the coast using the measured data as well as estimating the shoaling
coefficient for all events.
Project methodology
The MATLAB r2018a software is used to perform the analysis and illustrate different attributes
of the swell waves being reviewed. It loads the data obtained from the storm data to analyze the
different dynamics of the signal.
INTRODUCTION
Basic overview
Ocean waves are formed when the energy moves through a medium it is termed to be a
progressive wave. Progressive waves arise from forces that transmit energy through the water
columns or on the surface. Waves classification is based on the attributes namely period,
wavelength, frequency and distributing forces. Ocean swells are the long wavelength surface
wave groups with tend to travel long distances and are more stable than the wind waves. The
swells move from different parts of the ocean to the shoreline.
Problem statement
For analysis purposes, a submerged pressure sensor can be used as a wave gauge. It is
implemented to detect the wave induced dynamic pressure. In the analysis, a swell wave that has
deep water attributes propagates orthogonally towards a straight shoreline. During the analysis,
data was collected from about 5 storm events. There is need to develop a model to estimate the
swell wave height at the coast using the measured data as well as estimating the shoaling
coefficient for all events.
Project methodology
The MATLAB r2018a software is used to perform the analysis and illustrate different attributes
of the swell waves being reviewed. It loads the data obtained from the storm data to analyze the
different dynamics of the signal.

LITERATURE REVIEW
The ocean has both deep water and surface waves. The deep-water waves get into contact
with the sea bed and they tend to propagate and diminish within the deep-water columns and its
propagation is not affected by the seafloor. On the other hand, the surface waves are caused by
natural features such as the moon or sun through the wind. The formation of the wave is by an
external force which causes a ripple to form at some point in the ocean, the energy is transmitted
through swell waves to the shoreline. The energy is transmitted through the wave particles which
move until they form swell waves.
Figure 1 From calm to Fully Developed Sea [Source: Ocean Waves cptr-10]
To obtain the wavelength of an ocean wave,
λo= T2 g
2 π , … . fundamental wavelength
The wave energy is obtained such that the energy increases proportionally as the square of the
wave height. This is given as,
E=1
8 pg H 2 , g=9.8 m/s2
The wave steepness is given as,
S= H
λ
The ocean has both deep water and surface waves. The deep-water waves get into contact
with the sea bed and they tend to propagate and diminish within the deep-water columns and its
propagation is not affected by the seafloor. On the other hand, the surface waves are caused by
natural features such as the moon or sun through the wind. The formation of the wave is by an
external force which causes a ripple to form at some point in the ocean, the energy is transmitted
through swell waves to the shoreline. The energy is transmitted through the wave particles which
move until they form swell waves.
Figure 1 From calm to Fully Developed Sea [Source: Ocean Waves cptr-10]
To obtain the wavelength of an ocean wave,
λo= T2 g
2 π , … . fundamental wavelength
The wave energy is obtained such that the energy increases proportionally as the square of the
wave height. This is given as,
E=1
8 pg H 2 , g=9.8 m/s2
The wave steepness is given as,
S= H
λ
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

It is also referred to as the relative water peth.
For deep water analysis, the deep-water buoy records were obtained from the pressure
measurement to determine the wave characteristics. To determine the wave height,
H= Pmax +Pmin
2 pg
The dispersion relation equation is used in the MATLAB implementation to determine the
wavelength of the swell wave near or at the coast line,
λ=λo tanh ( 2 dπ
λ )
To obtain the wave number for the wave near the shoreline,
k = 2 π
λ , … wave number
K p =cosh ( k ( z +h ) )
cosh ( kh )
To obtain the wave celerity,
C= λ
T
To obtain the wave group velocity attribute of the deep-wave,
c g1= λo
2T
The wave group velocity for the coastal region is given as,
c g2=
(1+ ( 2 kH
sinh ( 2 kH ) ))∗λf
2 T
The shoaling coefficient is given as,
Ks = √ c g1
c g2
RESULTS AND DISCUSSION
The table below has results obtained from the 5 storm events in the analysis of the swell wave,
For deep water analysis, the deep-water buoy records were obtained from the pressure
measurement to determine the wave characteristics. To determine the wave height,
H= Pmax +Pmin
2 pg
The dispersion relation equation is used in the MATLAB implementation to determine the
wavelength of the swell wave near or at the coast line,
λ=λo tanh ( 2 dπ
λ )
To obtain the wave number for the wave near the shoreline,
k = 2 π
λ , … wave number
K p =cosh ( k ( z +h ) )
cosh ( kh )
To obtain the wave celerity,
C= λ
T
To obtain the wave group velocity attribute of the deep-wave,
c g1= λo
2T
The wave group velocity for the coastal region is given as,
c g2=
(1+ ( 2 kH
sinh ( 2 kH ) ))∗λf
2 T
The shoaling coefficient is given as,
Ks = √ c g1
c g2
RESULTS AND DISCUSSION
The table below has results obtained from the 5 storm events in the analysis of the swell wave,
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Deep Water Buoy Record Pressure Sensor at the Coast
Ho (m) To (m) Pmin (kPa) Pmax (kPa)
1 1.8 25 82.4 106.7
2 1.3 15 83.2 96.2
3 2.2 18 80.6 106.2
4 1.8 12 82.2 98.2
5 6.2 7 83.6 120.6
Matlab Implementation
Question 1
Part 1: computing the wave characteristics
clc
clear
close all
format short
%% computing wave characteristics
% 5 storm wave data
Ho = [1.8,1.3,2.2,1.8,6.2]; %Deep water buoy record (meters)
To = [25,15,18,12,7]; %Deep water Buoy record (Time in seconds)
Pmin=[82.4,83.2,80.6,82.2,83.6]; %Minimum pressure recorded by pressure
%sensor at the coast
Pmax =[106.7,96.2,106.2,98.2,120.6]; %Maximum pressure recorded by pressure
%sensor at the coast
g=9.81; % m/s^2
p=1026; % Density of seawater in kg/m^3
WaveHeight=(Pmax+Pmin)/(2*p*g); % Wave Height in deep water
WLo=(g*T.^2)/(2*pi); % Fundamental wavelength
Part 2: Shoaling coefficient using linear wave theory
%% To determine a function for d and T values: Using Bisection Algorithm
for j=1:length(To)
r=@(L)L-g*To(j)^2/2/pi*tanh(2*pi*WaveHeight(j)/L);
rf(j)=fzero(r,WLo(j))
end
%% To display the loop outputs
for i=1:5
k(i)=2*pi/rf(i) ;
kp(i)=1/cosh(k(i)*WaveHeight(i));
H(i)= (Pmax(i)-Pmin(i))/(p*g*kp(i)); %wave height
end
Ho (m) To (m) Pmin (kPa) Pmax (kPa)
1 1.8 25 82.4 106.7
2 1.3 15 83.2 96.2
3 2.2 18 80.6 106.2
4 1.8 12 82.2 98.2
5 6.2 7 83.6 120.6
Matlab Implementation
Question 1
Part 1: computing the wave characteristics
clc
clear
close all
format short
%% computing wave characteristics
% 5 storm wave data
Ho = [1.8,1.3,2.2,1.8,6.2]; %Deep water buoy record (meters)
To = [25,15,18,12,7]; %Deep water Buoy record (Time in seconds)
Pmin=[82.4,83.2,80.6,82.2,83.6]; %Minimum pressure recorded by pressure
%sensor at the coast
Pmax =[106.7,96.2,106.2,98.2,120.6]; %Maximum pressure recorded by pressure
%sensor at the coast
g=9.81; % m/s^2
p=1026; % Density of seawater in kg/m^3
WaveHeight=(Pmax+Pmin)/(2*p*g); % Wave Height in deep water
WLo=(g*T.^2)/(2*pi); % Fundamental wavelength
Part 2: Shoaling coefficient using linear wave theory
%% To determine a function for d and T values: Using Bisection Algorithm
for j=1:length(To)
r=@(L)L-g*To(j)^2/2/pi*tanh(2*pi*WaveHeight(j)/L);
rf(j)=fzero(r,WLo(j))
end
%% To display the loop outputs
for i=1:5
k(i)=2*pi/rf(i) ;
kp(i)=1/cosh(k(i)*WaveHeight(i));
H(i)= (Pmax(i)-Pmin(i))/(p*g*kp(i)); %wave height
end
%% To obtain the figure of Water Depth and Shoaling Coefficient
WG2=(1+(2.*k.*WaveHeight./sinh (2.*k.*WaveHeight)).*rf./(2.*To)); % Wave group
velocity in shallow water
ShoalingCoeff=sqrt(Wavegroup./WG2);
% relative water depth
ds=WaveHeight./rf;
Part 3: graphical illustrations
-5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1
Relative Water Depth 10-3
2.5
3
3.5
4
4.5
5
Shoaling Coefficient
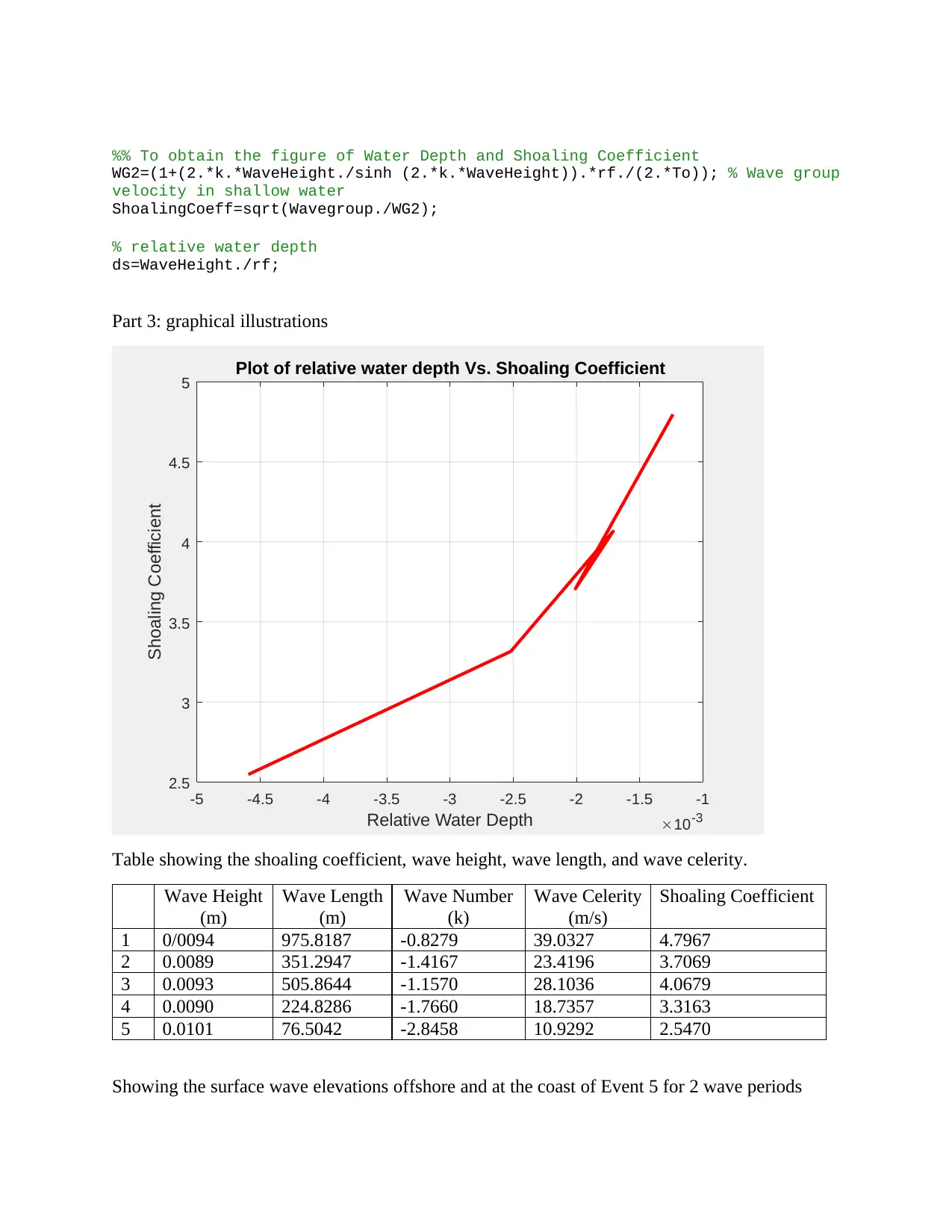
Plot of relative water depth Vs. Shoaling Coefficient
Table showing the shoaling coefficient, wave height, wave length, and wave celerity.
Wave Height
(m)
Wave Length
(m)
Wave Number
(k)
Wave Celerity
(m/s)
Shoaling Coefficient
1 0/0094 975.8187 -0.8279 39.0327 4.7967
2 0.0089 351.2947 -1.4167 23.4196 3.7069
3 0.0093 505.8644 -1.1570 28.1036 4.0679
4 0.0090 224.8286 -1.7660 18.7357 3.3163
5 0.0101 76.5042 -2.8458 10.9292 2.5470
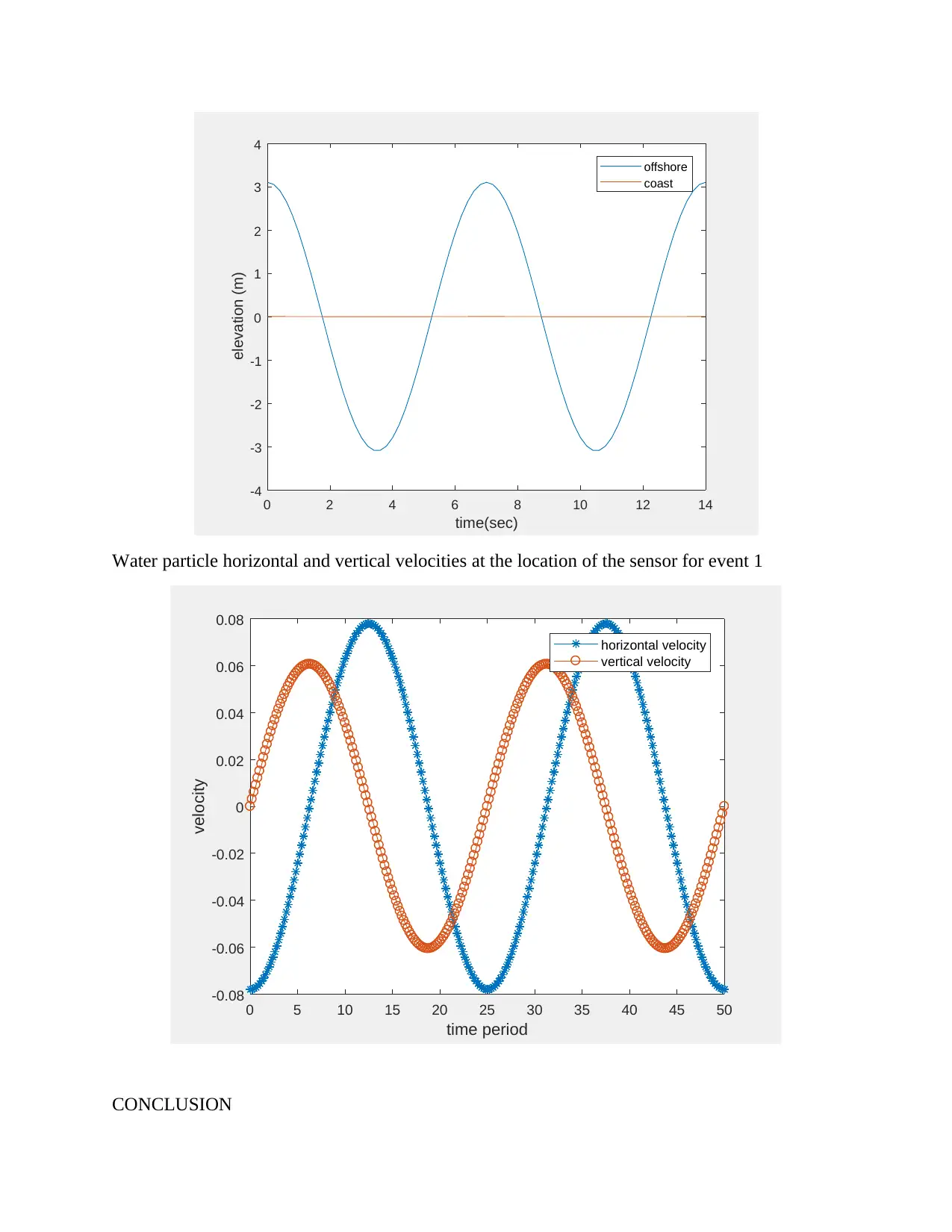
Showing the surface wave elevations offshore and at the coast of Event 5 for 2 wave periods
WG2=(1+(2.*k.*WaveHeight./sinh (2.*k.*WaveHeight)).*rf./(2.*To)); % Wave group
velocity in shallow water
ShoalingCoeff=sqrt(Wavegroup./WG2);
% relative water depth
ds=WaveHeight./rf;
Part 3: graphical illustrations
-5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1
Relative Water Depth 10-3
2.5
3
3.5
4
4.5
5
Shoaling Coefficient
Plot of relative water depth Vs. Shoaling Coefficient
Table showing the shoaling coefficient, wave height, wave length, and wave celerity.
Wave Height
(m)
Wave Length
(m)
Wave Number
(k)
Wave Celerity
(m/s)
Shoaling Coefficient
1 0/0094 975.8187 -0.8279 39.0327 4.7967
2 0.0089 351.2947 -1.4167 23.4196 3.7069
3 0.0093 505.8644 -1.1570 28.1036 4.0679
4 0.0090 224.8286 -1.7660 18.7357 3.3163
5 0.0101 76.5042 -2.8458 10.9292 2.5470
Showing the surface wave elevations offshore and at the coast of Event 5 for 2 wave periods
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
0 2 4 6 8 10 12 14
time(sec)
-4
-3
-2
-1
0
1
2
3
4
elevation (m)
offshore
coast
Water particle horizontal and vertical velocities at the location of the sensor for event 1
0 5 10 15 20 25 30 35 40 45 50
time period
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
velocity
horizontal velocity
vertical velocity
CONCLUSION
time(sec)
-4
-3
-2
-1
0
1
2
3
4
elevation (m)
offshore
coast
Water particle horizontal and vertical velocities at the location of the sensor for event 1
0 5 10 15 20 25 30 35 40 45 50
time period
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
velocity
horizontal velocity
vertical velocity
CONCLUSION
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

QUESTION 2
INTRODUCTION
Overview
Marine sediments are records taken on the amounts of sediment at the ocean shoreline
over a number of years. The sediments could be as a result of the eroded rock particles and
fragments which are transported to the ocean and they are deposited by settling through water
columns. Sediments are lithogenous, derived from land, biogenous, derived from organisms,
authigenic, derived from water, and cosmogenous, derived from the outer space. There are
morphological developments caused as a result of waves, winds, currents, and sea level changes
in the ocean.
Problem statement
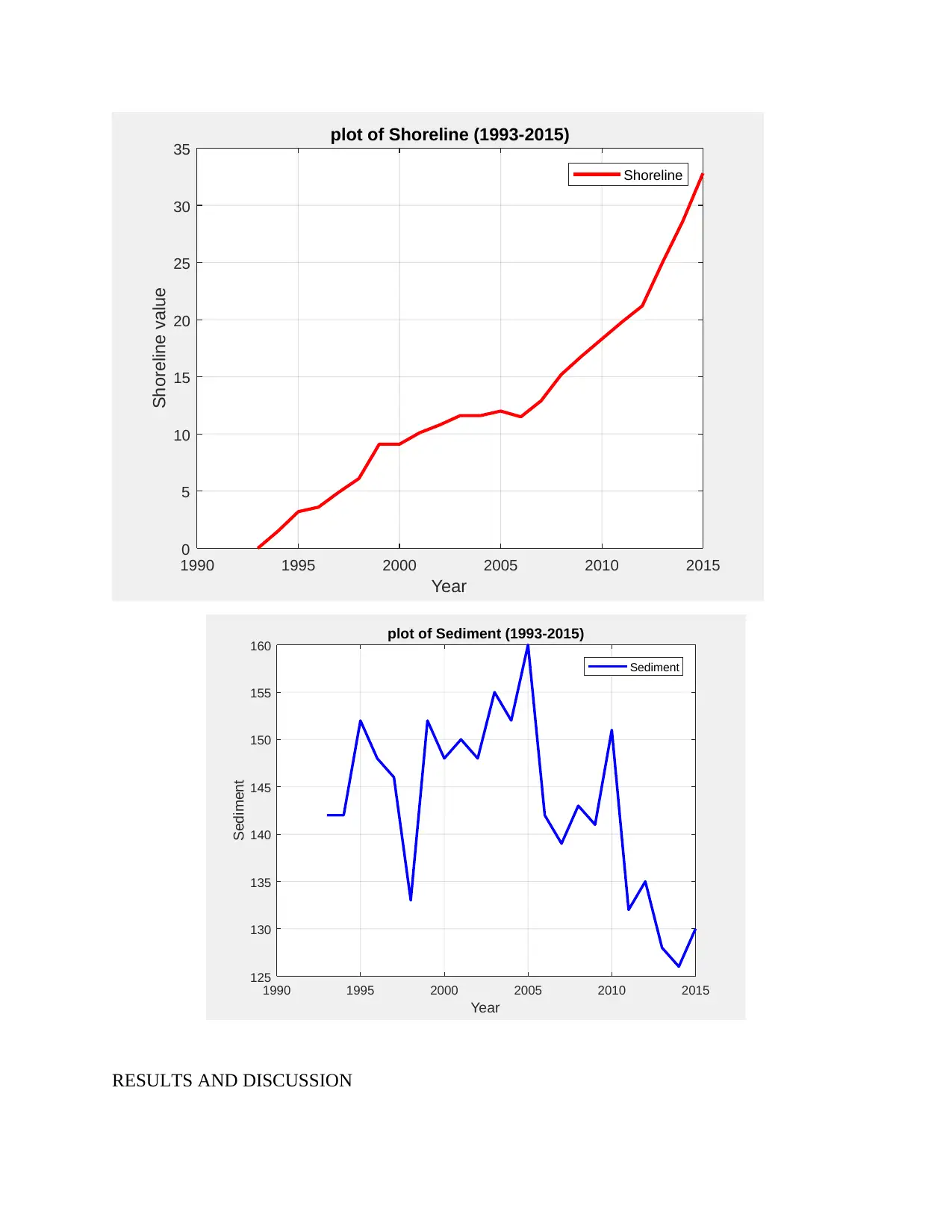
The sediment transport rates between the years 1993 to 2015 were collected and save in a
spreadsheet file. The domain contained no sinks and sources for the sediment transport.
Similarly, aerial views of the shoreline within this period were collected and saved. The case
study in this analysis report considers a 5 km stretch of coast situated in the North-South
Direction while the ocean is at the east of the shoreline. The illustration below gives a clear
image,
INTRODUCTION
Overview
Marine sediments are records taken on the amounts of sediment at the ocean shoreline
over a number of years. The sediments could be as a result of the eroded rock particles and
fragments which are transported to the ocean and they are deposited by settling through water
columns. Sediments are lithogenous, derived from land, biogenous, derived from organisms,
authigenic, derived from water, and cosmogenous, derived from the outer space. There are
morphological developments caused as a result of waves, winds, currents, and sea level changes
in the ocean.
Problem statement
The sediment transport rates between the years 1993 to 2015 were collected and save in a
spreadsheet file. The domain contained no sinks and sources for the sediment transport.
Similarly, aerial views of the shoreline within this period were collected and saved. The case
study in this analysis report considers a 5 km stretch of coast situated in the North-South
Direction while the ocean is at the east of the shoreline. The illustration below gives a clear
image,

To perform a sediment transport analysis, a numerical model must be developed to compute the
location of the shoreline between the years 1993 to 2015.
LITERATURE REVIEW
The rate at which the shoreline erodes or retreats towards the mainland is obtained as,
( 1− p ) ( hc+ B ) ∂ x s
∂t =−Qx + ∂Q y
∂ y +Qsink −Qsource
Qy= K
16 ( s−1 ) √ γ √ g H b
5
2 sin 2θb
Parameter Value
Stretch of coast 5 km
Breaker Height (southern end) 1.4 m
Breaker Angle (southern end) 100
Breaker Parameter γb 0.8
Breaker Angle (Northern end) 1.45 m
Beach Profile (break point) 1/40
Sand -Quartz S=2.63 p=0.28 grain size=0.22
Bern Height 3 m AHD
Measurable seasonal bed level changes 6 m
The long shore transport rate is given by,
∂Q y
∂ y = Qy , s−Q y, n
dy ∗dt
The partial differential equation demonstrates the transportation of the sediment in the longshore
case study which is obtained by showing the direction of the wave which flows from the East-
South-East and moves from South to North.
Numerical solutions
location of the shoreline between the years 1993 to 2015.
LITERATURE REVIEW
The rate at which the shoreline erodes or retreats towards the mainland is obtained as,
( 1− p ) ( hc+ B ) ∂ x s
∂t =−Qx + ∂Q y
∂ y +Qsink −Qsource
Qy= K
16 ( s−1 ) √ γ √ g H b
5
2 sin 2θb
Parameter Value
Stretch of coast 5 km
Breaker Height (southern end) 1.4 m
Breaker Angle (southern end) 100
Breaker Parameter γb 0.8
Breaker Angle (Northern end) 1.45 m
Beach Profile (break point) 1/40
Sand -Quartz S=2.63 p=0.28 grain size=0.22
Bern Height 3 m AHD
Measurable seasonal bed level changes 6 m
The long shore transport rate is given by,
∂Q y
∂ y = Qy , s−Q y, n
dy ∗dt
The partial differential equation demonstrates the transportation of the sediment in the longshore
case study which is obtained by showing the direction of the wave which flows from the East-
South-East and moves from South to North.
Numerical solutions
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

To develop the numerical model in Matlab, first the relationship between the data obtained and
the shoreline condition was plotted,
%% reading values from sediment and shoreline spreadsheet files
sediment=xlsread('sediment.xls','A1:B24')
shoreline=xlsread('shoreline.xls','A1:B24');
year=sediment(1:23)
sedimentval=sediment(24:46)
shorelineval=shoreline(24:46)
figure(1)
plot(year,sedimentval,'b','LineWidth',2)
title('plot of Sediment (1993-2015)')
legend('Sediment')
xlabel('Year')
ylabel('Sediment')
grid on
figure(2)
plot(year,shorelineval,'r','LineWidth',2)
title('plot of Shoreline (1993-2015)')
legend('Shoreline')
xlabel('Year')
ylabel('Shoreline value')
grid on
the shoreline condition was plotted,
%% reading values from sediment and shoreline spreadsheet files
sediment=xlsread('sediment.xls','A1:B24')
shoreline=xlsread('shoreline.xls','A1:B24');
year=sediment(1:23)
sedimentval=sediment(24:46)
shorelineval=shoreline(24:46)
figure(1)
plot(year,sedimentval,'b','LineWidth',2)
title('plot of Sediment (1993-2015)')
legend('Sediment')
xlabel('Year')
ylabel('Sediment')
grid on
figure(2)
plot(year,shorelineval,'r','LineWidth',2)
title('plot of Shoreline (1993-2015)')
legend('Shoreline')
xlabel('Year')
ylabel('Shoreline value')
grid on
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
1990 1995 2000 2005 2010 2015
Year
0
5
10
15
20
25
30
35
Shoreline value
plot of Shoreline (1993-2015)
Shoreline
1990 1995 2000 2005 2010 2015
Year
125
130
135
140
145
150
155
160
Sediment
plot of Sediment (1993-2015)
Sediment
RESULTS AND DISCUSSION
Year
0
5
10
15
20
25
30
35
Shoreline value
plot of Shoreline (1993-2015)
Shoreline
1990 1995 2000 2005 2010 2015
Year
125
130
135
140
145
150
155
160
Sediment
plot of Sediment (1993-2015)
Sediment
RESULTS AND DISCUSSION
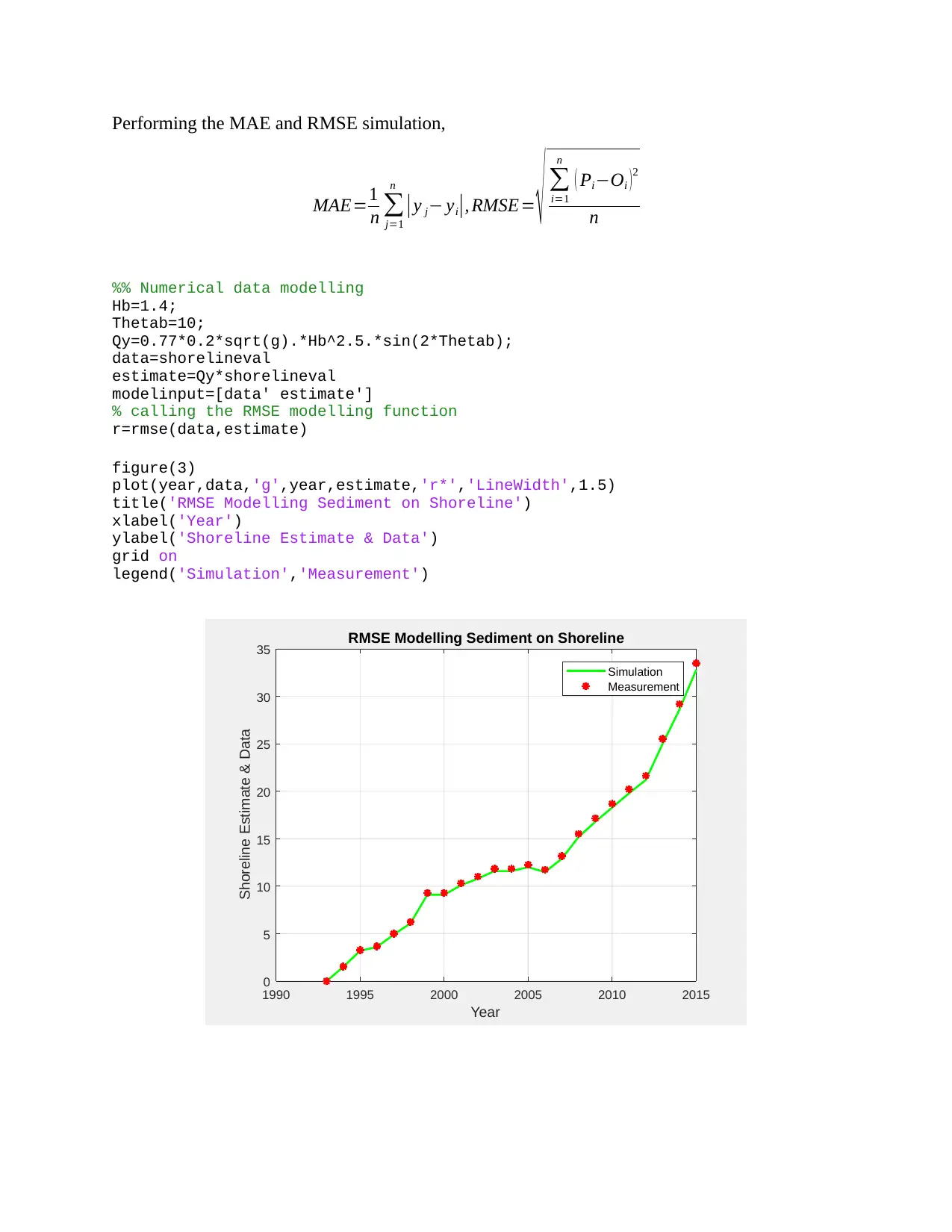
Performing the MAE and RMSE simulation,
MAE=1
n ∑
j=1
n
| y j− yi|, RMSE= √ ∑
i=1
n
( Pi−Oi ) 2
n
%% Numerical data modelling
Hb=1.4;
Thetab=10;
Qy=0.77*0.2*sqrt(g).*Hb^2.5.*sin(2*Thetab);
data=shorelineval
estimate=Qy*shorelineval
modelinput=[data' estimate']
% calling the RMSE modelling function
r=rmse(data,estimate)
figure(3)
plot(year,data,'g',year,estimate,'r*','LineWidth',1.5)
title('RMSE Modelling Sediment on Shoreline')
xlabel('Year')
ylabel('Shoreline Estimate & Data')
grid on
legend('Simulation','Measurement')
1990 1995 2000 2005 2010 2015
Year
0
5
10
15
20
25
30
35
Shoreline Estimate & Data
RMSE Modelling Sediment on Shoreline
Simulation
Measurement
MAE=1
n ∑
j=1
n
| y j− yi|, RMSE= √ ∑
i=1
n
( Pi−Oi ) 2
n
%% Numerical data modelling
Hb=1.4;
Thetab=10;
Qy=0.77*0.2*sqrt(g).*Hb^2.5.*sin(2*Thetab);
data=shorelineval
estimate=Qy*shorelineval
modelinput=[data' estimate']
% calling the RMSE modelling function
r=rmse(data,estimate)
figure(3)
plot(year,data,'g',year,estimate,'r*','LineWidth',1.5)
title('RMSE Modelling Sediment on Shoreline')
xlabel('Year')
ylabel('Shoreline Estimate & Data')
grid on
legend('Simulation','Measurement')
1990 1995 2000 2005 2010 2015
Year
0
5
10
15
20
25
30
35
Shoreline Estimate & Data
RMSE Modelling Sediment on Shoreline
Simulation
Measurement
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 13
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.

