University Homework Solution: Complex Analysis Assignment - Math 301

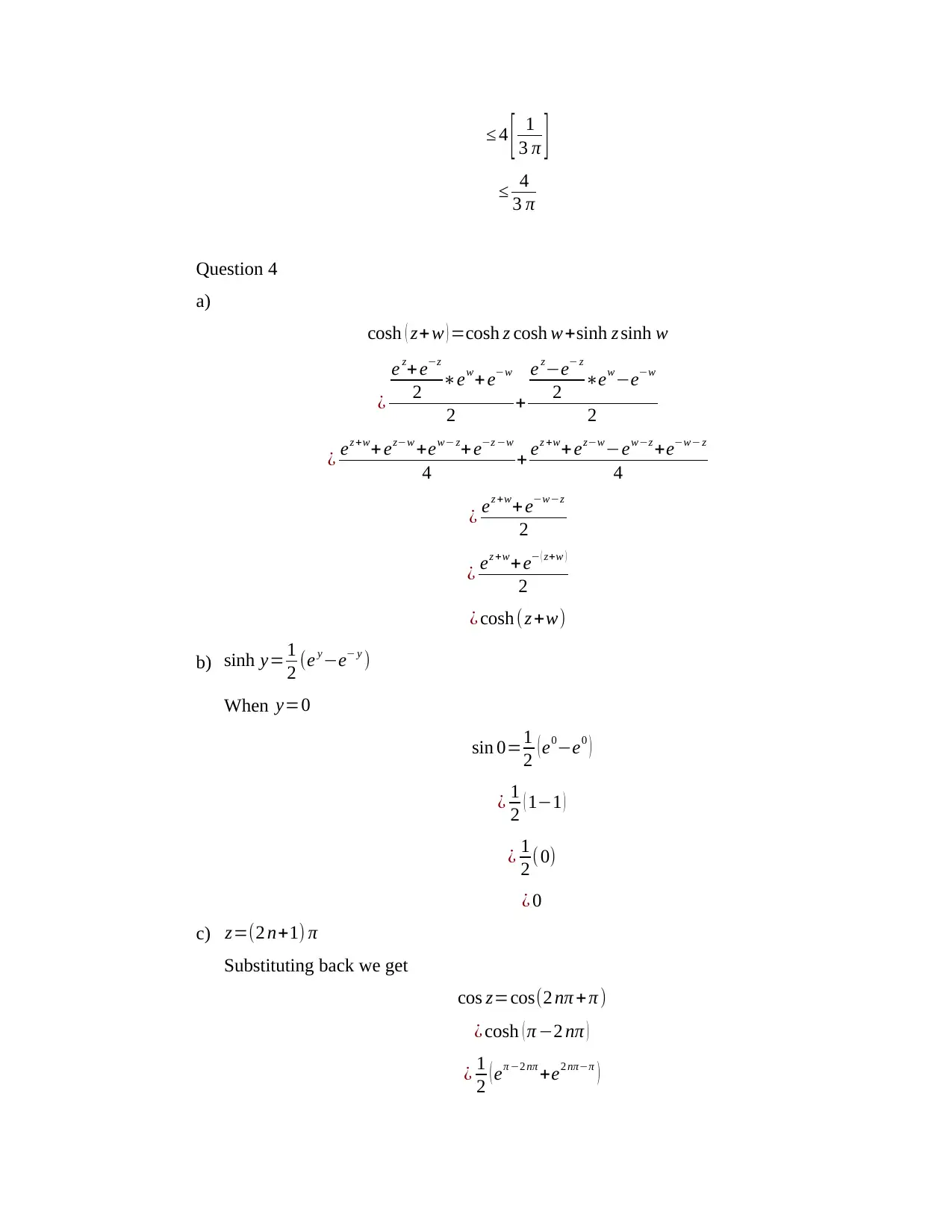
This document provides a comprehensive solution to a complex analysis homework assignment. The solution covers several key concepts including the continuity and differentiability of complex functions, properties of complex exponentials, and evaluation of complex integrals. The assignment includes problems related to the behavior of functions in the complex plane, such as determining whether a function is analytic and finding the inverse of a complex function. The solution demonstrates the application of Cauchy-Riemann equations, the use of partial fraction decomposition, and techniques for evaluating complex integrals along specified paths. The solution uses concepts like the chain rule and the properties of complex logarithms and exponentials. The references include citations to relevant textbooks and publications used to support the solutions.

Question 1
a) f ( z )= 3
2 ℜ(z )
To show that it is continuous, we follow the following steps;
lim
z → z0
( 3
2 ℜ )= lim
x→ x0
(3
2 x )
¿ lim
x→ x0
3
2 x−3
2 x0
x−x0
( x−x0 ) + 3
2 x0
¿ 3
2 xo
¿ 3
2 ℜ( z0 )
Thus, f (z) is continuous at all points.
To show that it is not differentiable at any point;
f '
( z0 ) ≠ d
dz ( 3
2 ℜ ( z0 ) ) CITATION Ver11 \l 2057 (Vera Pawlowsky-Glahn, 2011)
d
dz ( 3
2 ℜ ( z0 ))= lim
x → x0
3
2 x −3
2 x0
x −x0
¿ 0
Hence, it is not differentiable at any point.
Question 2
a) False.
Complex number z=x +iy will lie inside the unit circle when x2+ y2<1.
b) True;
ez ≠ 1; so it has no singularity. Therefore, f is analytic as well as meromorphic.
c) False.
ez :C → C is neither injective nor surjective. It is not injective because
ez +2 πik =ez √ k ∈ z. It is not surjective because ez ≠ 0. Hence domain will be 2 πiz and
the range C /{0 }.
d) False.

Sing chain rule d
dz ( elog z ) ¿z= z0
= elog z
z0
Question 3
a)
i) ∫
Γ
❑ 1
2 e3 iz dz
The path of integration has length L=2 π. We follow by seeking an upper bound M
for the function 1
2 e3 iz
when |z|=2 and z=x +iy CITATION Mat18 \l 2057 (Matthias
Beck, 2018)
|1
2 e3 iz
|=|1
2 e3 i ( x+iy )
|
¿ 1
2 e3ix −3 y
≤ e6 i
2
Hence, ∫
Γ
❑ 1
2 e3 iz dz = e6 i
2
ii) ∫
Γ
❑ 2
z dz
The path of integration has L=4 π. We follow by seeking the upper bound M of 2
z
when |z|=1 and z=2+2 i
|z|=¿ 2+2i∨¿
¿ 2
Thus ∫
Γ
❑ 2
z dz ≤ 2
2 =1
b) γ ( t ) =e¿
Integrating we get γ' ( t )= ln t
i
Hence
∫
γ
❑ 1
z + 1
4
dz =∫
0
π
( 1
e¿+ 1
4 )( 1
i e¿+ 1
4 ) dt

≤ 4 [ 1
3 π ]
≤ 4
3 π
Question 4
a)
cosh ( z+ w ) =cosh z cosh w+sinh z sinh w
¿
e z+ e−z
2 ∗ew+e−w
2 +
e z−e− z
2 ∗ew−e−w
2
¿ ez +w+ ez−w +ew− z+ e−z −w
4 + ez +w+ ez−w−ew−z +e−w− z
4
¿ ez +w+ e−w−z
2
¿ ez +w+e− ( z+w )
2
¿ cosh ( z +w)
b) sinh y= 1
2 (e y−e− y )
When y=0
sin 0=1
2 ( e0−e0 )
¿ 1
2 ( 1−1 )
¿ 1
2 (0)
¿ 0
c) z=(2 n+1) π
Substituting back we get
cos z=cos(2 nπ + π )
¿ cosh ( π −2 nπ )
¿ 1
2 ( eπ −2 nπ +e2 nπ−π )

¿ 1
2 (−1+−1)
¿ 1
2 (−2 )
¿−1
To show that 1
1+ cosh z has double poles at z=(2 n+1) π, we substitute the value of z s below.
1
1+ cosh z = 1
1+ cosh (2 nπi+πi)
¿ 1
1+ 1
2 (e2 nπi+ πi+ e− (2 nπi+πi ))
Simplifying;
1
1+ cosh z = 2
2+e2 nπi+ πi+e− (2 nπi+πi )
Question 5
a) ∂ u
∂ x = ∂ v
∂ y
∂ v
∂ x =−∂ u
∂ y
f ' ( z )= ∂ u
∂ x +i ∂ v
∂ x
¿ ∂ v
∂ y −i ∂u
∂ y
b) f is differentiable in an open set D and f ' ( z )=0
f ' ( z0 ) =f ' (x0 +i y0)
¿ lim
h→ 0
u ( x0 +h , y0 )−u ( x0 , y0 ) +i [ v ( x0 +h , y0 ) −v ( x0 , yo ) ]
h

¿ ux ( x0 , y0 ) +i vx (x0 , y0 )
Hence, ux=uy=v x=v y=0
Since f :C → C is differentiable in D and f (z) is real for all z ∈ C, then f is a constant
function.
c) For a function to be differentiable, it must satisfy the Cauchy-Riemann’s equation
f ( z ) =u+iv
And also satisfy
ux=uy
uy =−v x
For f ( z ) =ℜ ( z ) . exp ( z ) we get
f ' ( z )=lim
h →0
( x +h ) ex +h+iy −x ex+iy
h
We obtain that
ux=1≠ v y=0
So it is not differentiable.
Question 7
a) ∫
−∞
+∞
x2
( x2+ 1 )( x2 + 4 ) dx
Taking the partial fraction of the equation we get
∫
−∞
+∞
x2
( x2+1 ) ( x2 +4 ) dx=∫
−∞
+ ∞
[ 4
3 ( x2+4)− 1
3( x2+1) ] dx
¿ ∫
−∞
+∞
4
3( x2 + 4) dx−∫
−∞
+∞
1
3(x2+1) dx
¿ [ 2
3 tan−1
( x
2 ) ]−∞
+∞
− [ 1
3 tan−1 x ]−∞
+ ∞
¿ π
6 −−π
6
¿ π
3

b) ∫
−∞
+∞
e3 ix
x2+1 dx
Factoring the denominator
∫
−∞
+∞
e3 ix
x2+1 dx=∫
−∞
+∞
e3 ix
( x−i ) ( x+i ) dx
Performing partial fraction decomposition
¿ ∫
−∞
+∞
( ie3 ix
2( x +i)− ie3 ix
2(x+ i) ) dx
Applying linearity,
¿ i
2 ∫
−∞
+ ∞
e3ix
x +i dx− i
2 ∫
−∞
+∞
e3 ix
x−i dx
Solving by double integration
¿ e3 iE (3 ix−3)
2 − e−3 iEi ( 3 ix+3 )
2 + C
Question7
a) p ( x ) =an xn+ an−1 xn −1 +… ..+a1 x +a0
Take that the coefficients an … a0 all belong to F √ k. For l=0,1,2 … n we have
al=α l+ βl √ k
Since a is a root of p(x ), we have
p ( a ) = (αn+ βn √k ) an + (α n−1+ βn−1 √k ) an−1 +… ..+ ( α1 + β1 √k ) a+ ( α0 +β0 √k )
Suppose the polynomial has coefficients in the field Q and it has a constructible root a.
There is a chain of subfield R with Q=F1 ⊂ F2 ⊂ …. ⊂ Fn−1 ⊂ Fn
With each subfield a quadratic extensive of previous one and a ∈ Fn. p(x ) has a root in
Fn−1. We reach to F1=Q hence p(x )has at least one real root.
b) x6 +1
Rewrite 1 as 13
x6 +1=x6 +13
Applying exponent rule
x6 +13= ( x2 )3
+13

Applying sum of cubes formula
( x2 )
3
+13=( x2 +1)(x4−x2 +1)
Hence, x6 +1=( x2 +1)(x4−x2 +1)

References
Matthias Beck, E. A., 2018. A First Course in Complex Analysis. In: s.l.:Orthogonal Publishing L3C, pp.
132-143.
Vera Pawlowsky-Glahn, A. B., 2011. Compositional Data Analysis: Theory and Applications. In: s.l.:John
Wiley & Sons, pp. 64-71.