Comprehensive Design Project: Analysis and Design of Slabs and Columns

This project focuses on the structural analysis and design of slabs and columns, adhering to Eurocode 2 (EC2) standards. It begins with an introduction to Reactive Powder Concrete (RPC) and Fiber Reinforced Concrete (FRC), discussing their properties and applications. The project then delves into load calculations for slabs and columns in multi-story buildings, considering dead loads, live loads, and self-slab loads. Detailed calculations are provided for both the 1st and 2nd slabs, including flexural reinforcement, shear design, and deflection checks. The design process includes determining the required steel reinforcement, checking for shear and punching shear, and ensuring the spacing and placement of reinforcement bars comply with design codes. The project also covers the design of interior columns, calculating column loads for various stories. Overall, the project offers a comprehensive guide to structural design principles, including load calculations, material properties, and compliance with design codes.

Contents
TASK 1............................................................................................................................................3
Introduction......................................................................................................................................5
TASK 2............................................................................................................................................9
For suitable analysis we have to do some basic calculation and then the final calculations as
follows...........................................................................................................................................11
DESIGN OF 1st Slab (EUROCODE 2, EC 2) ............................................................................12
DESIGN OF 2nd Slab (EUROCODE 2, EC 2)............................................................................14
Interior Column Designing...........................................................................................................18
Analysis of the behavior of the exterior column and showing the result thus reinforcement in
under consideration two processes................................................................................................19
CONCLUSION..............................................................................................................................22
Page | 1

Task 1
Introduction
Reactive powder concrete (RPC) has been created in the last two decades as Adding silica fume
enhances the probability of RPC decline and shrinking. Shrinking and creep may dramatically
affect the long-term characteristics of concrete. Shrinking and creeping may increase fracture
breadth and structural deformation in large-scale structures. It may also encourage stress
dissipation in the prestressed reinforcement component. It is thus vital to estimate and monitor
concrete shrinkage and creep. Many studies have been carried out in recent years to reduce and
squeeze typical strength concrete, generating sophisticated theories and models. However, a very
little investigation on RPC shrinking and creeping. Shamsad Ahmad et al. conducted three-day
water treatment shrinkage studies in the RPC and noticed a concentration reduction of water to
binding, cement and silica smoke. Nguyen found that the addition of RPC rice husk ash might
significantly reduce the autogenous decline of RPC. Furthermore, many other solutions such as
expansive additives, admixture reduction of gross cement particles and healing conditions have
been devised to reduce. Previous RPC research focused on RPC auto-reduction to the best
knowledge of the authors. The influence of RPC components on self-reduction has been
examined. In addition, many strategies concentrated on minimizing the autogenous decline of
RPC. In prefabricated components, RPC is commonly used. For commercial RPC, steam heat
treatment is typically used to speed up hydration and strength development, although much less
RPC shrinkage will be observed after heat treatment and creeping. Furthermore, since there is no
shrinking and declining RPC model for the RPC, most current shrinkage and shrinkage models
were produced by experimental data adaptation. They are perfect for conventional concrete
solidity rather than RPC. Check current RPC shrinkage and creep models.
In recent decades, one of the most promising kinds of concrete for both structural and non-
structural uses has been fibre-reinforced concrete (FRC), which is concrete constructed with steel
or polymer fibres that may give substantial technical and economic benefits. Studies using multi-
criteria decision-making methodologies that include social, environmental, and economic
sustainability have shown that FRC may be more sustainable than reinforced concrete (RC) for
many infrastructure projects where fiber utilization is technically feasible (as unique
reinforcement or in combination with traditional steel rebars). Given the enormous amount of
concrete produced globally, more than 25 billion tones, progress toward more sustainable
alternatives is critical. In developed nations, over half of all made concrete is utilised in
structural applications. As a result, the FRC is increasingly being employed in components
subjected to bending and long-term gravity resistance, such as ground-based slabs, floors,
Page | 2

roadways, tunnel lines, pipe sewage lines, and flat slabs. Thanks to extensive study, FRC
structural design has been incorporated in various design codes in recent years, including the
2010, ACI 318, Italian, and Spanish Codes. Until recently, however, research has mostly
concentrated on short-term material and structural qualities, leaving additional FRC design
concerns to be addressed in the early phases of development.
Page | 3

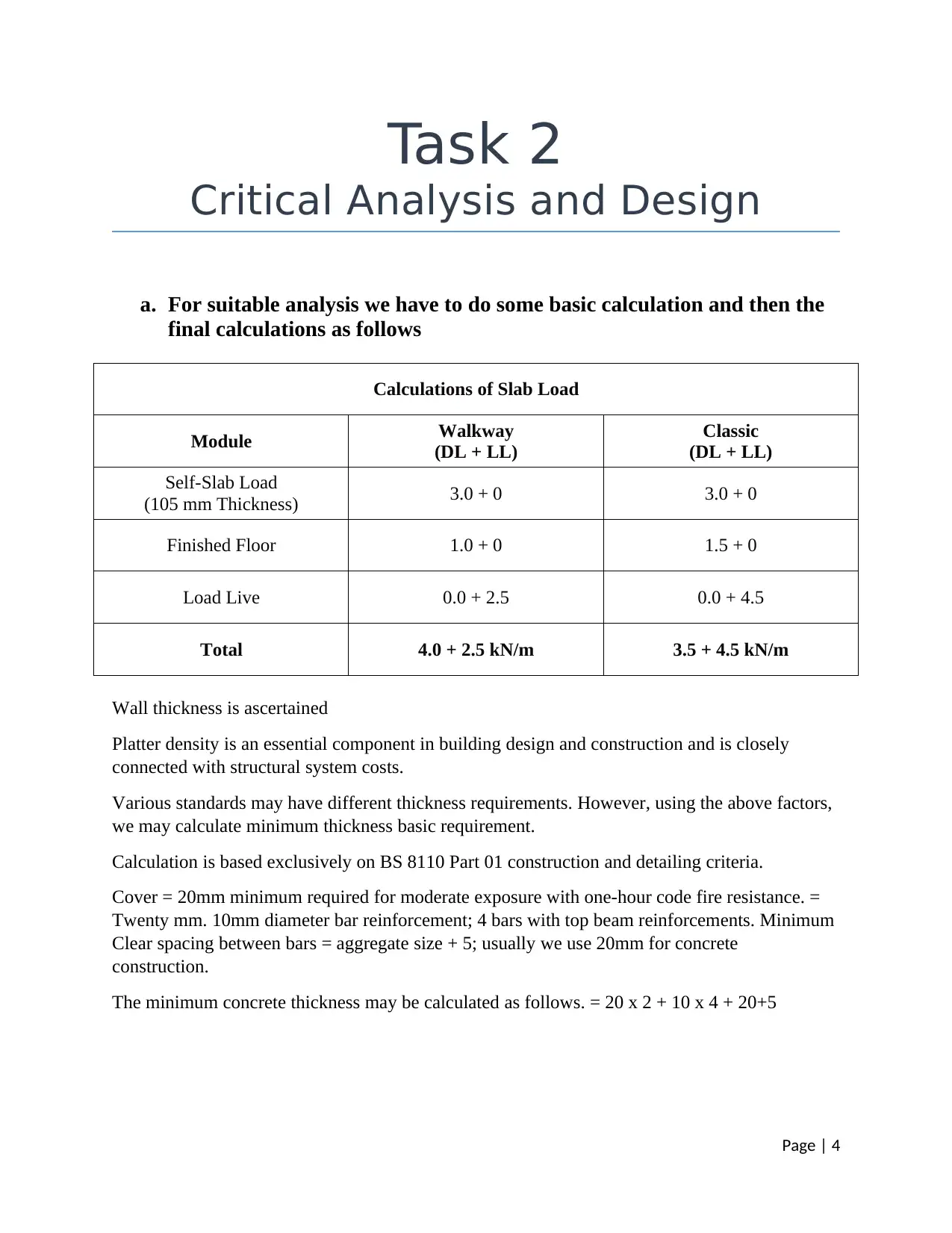
Task 2
Critical Analysis and Design
a. For suitable analysis we have to do some basic calculation and then the
final calculations as follows
Calculations of Slab Load
Module Walkway
(DL + LL)
Classic
(DL + LL)
Self-Slab Load
(105 mm Thickness) 3.0 + 0 3.0 + 0
Finished Floor 1.0 + 0 1.5 + 0
Load Live 0.0 + 2.5 0.0 + 4.5
Total 4.0 + 2.5 kN/m 3.5 + 4.5 kN/m
Wall thickness is ascertained
Platter density is an essential component in building design and construction and is closely
connected with structural system costs.
Various standards may have different thickness requirements. However, using the above factors,
we may calculate minimum thickness basic requirement.
Calculation is based exclusively on BS 8110 Part 01 construction and detailing criteria.
Cover = 20mm minimum required for moderate exposure with one-hour code fire resistance. =
Twenty mm. 10mm diameter bar reinforcement; 4 bars with top beam reinforcements. Minimum
Clear spacing between bars = aggregate size + 5; usually we use 20mm for concrete
construction.
The minimum concrete thickness may be calculated as follows. = 20 x 2 + 10 x 4 + 20+5
Page | 4

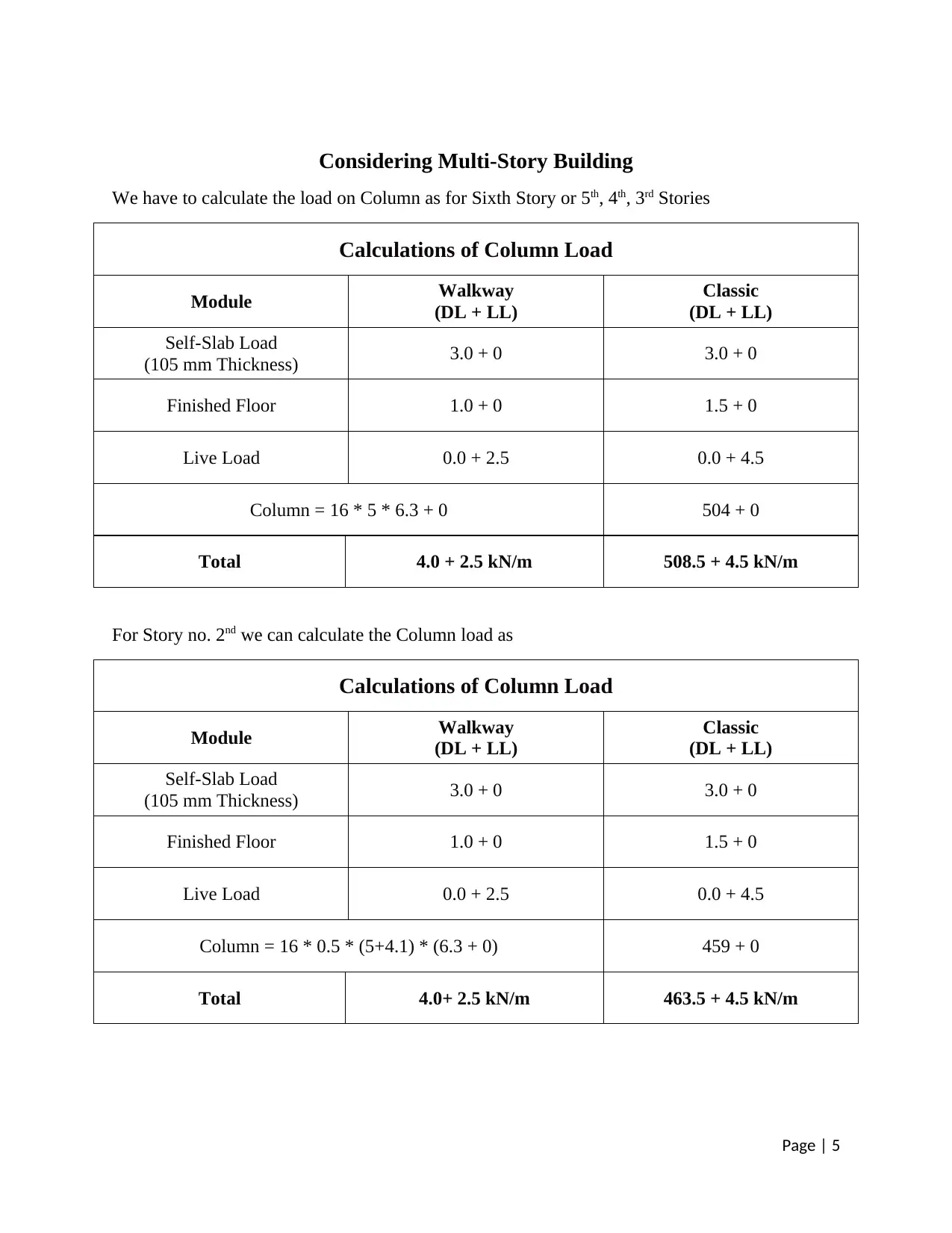
Considering Multi-Story Building
We have to calculate the load on Column as for Sixth Story or 5th, 4th, 3rd Stories
Calculations of Column Load
Module Walkway
(DL + LL)
Classic
(DL + LL)
Self-Slab Load
(105 mm Thickness) 3.0 + 0 3.0 + 0
Finished Floor 1.0 + 0 1.5 + 0
Live Load 0.0 + 2.5 0.0 + 4.5
Column = 16 * 5 * 6.3 + 0 504 + 0
Total 4.0 + 2.5 kN/m 508.5 + 4.5 kN/m
For Story no. 2nd we can calculate the Column load as
Calculations of Column Load
Module Walkway
(DL + LL)
Classic
(DL + LL)
Self-Slab Load
(105 mm Thickness) 3.0 + 0 3.0 + 0
Finished Floor 1.0 + 0 1.5 + 0
Live Load 0.0 + 2.5 0.0 + 4.5
Column = 16 * 0.5 * (5+4.1) * (6.3 + 0) 459 + 0
Total 4.0+ 2.5 kN/m 463.5 + 4.5 kN/m
Page | 5

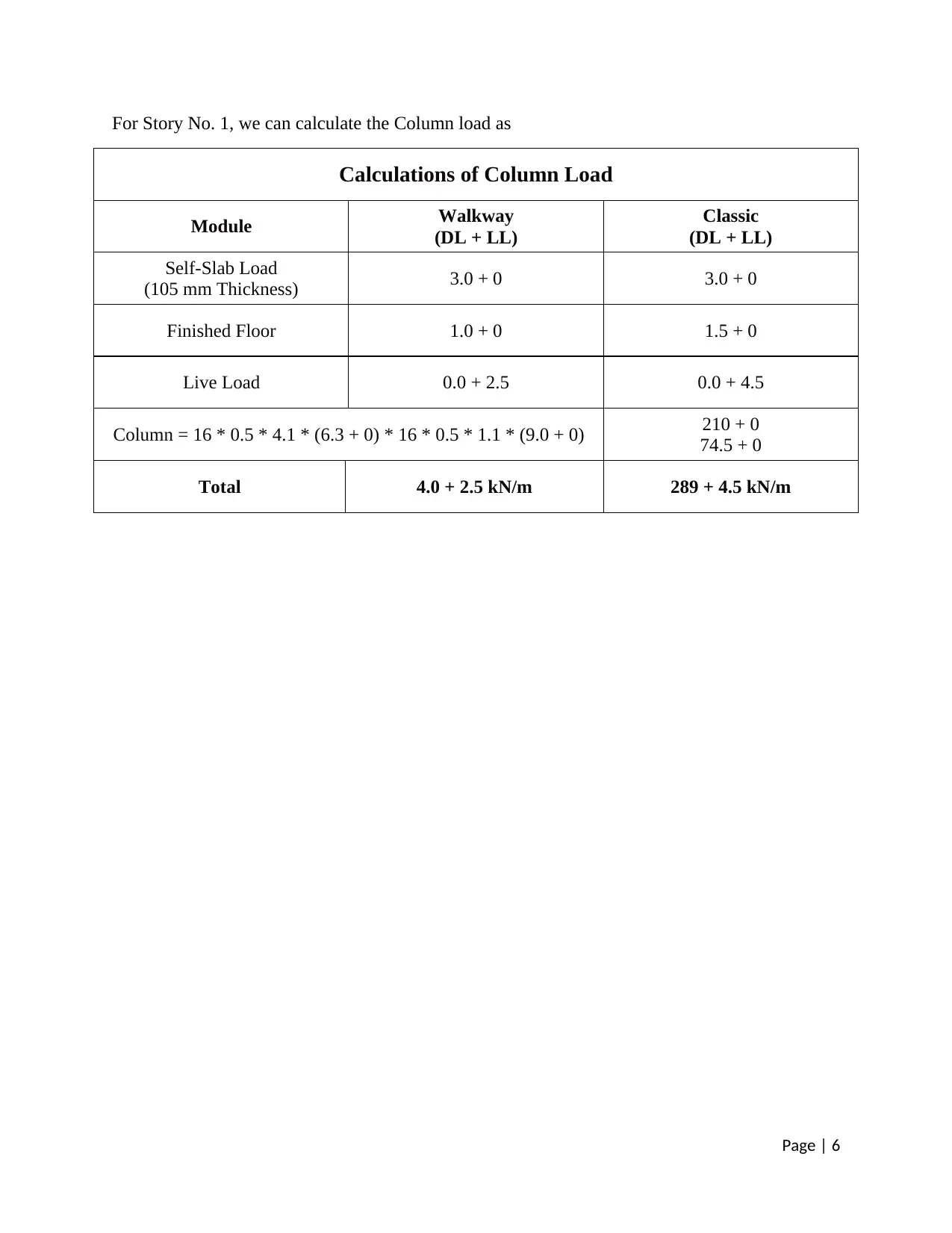
For Story No. 1, we can calculate the Column load as
Calculations of Column Load
Module Walkway
(DL + LL)
Classic
(DL + LL)
Self-Slab Load
(105 mm Thickness) 3.0 + 0 3.0 + 0
Finished Floor 1.0 + 0 1.5 + 0
Live Load 0.0 + 2.5 0.0 + 4.5
Column = 16 * 0.5 * 4.1 * (6.3 + 0) * 16 * 0.5 * 1.1 * (9.0 + 0) 210 + 0
74.5 + 0
Total 4.0 + 2.5 kN/m 289 + 4.5 kN/m
Page | 6

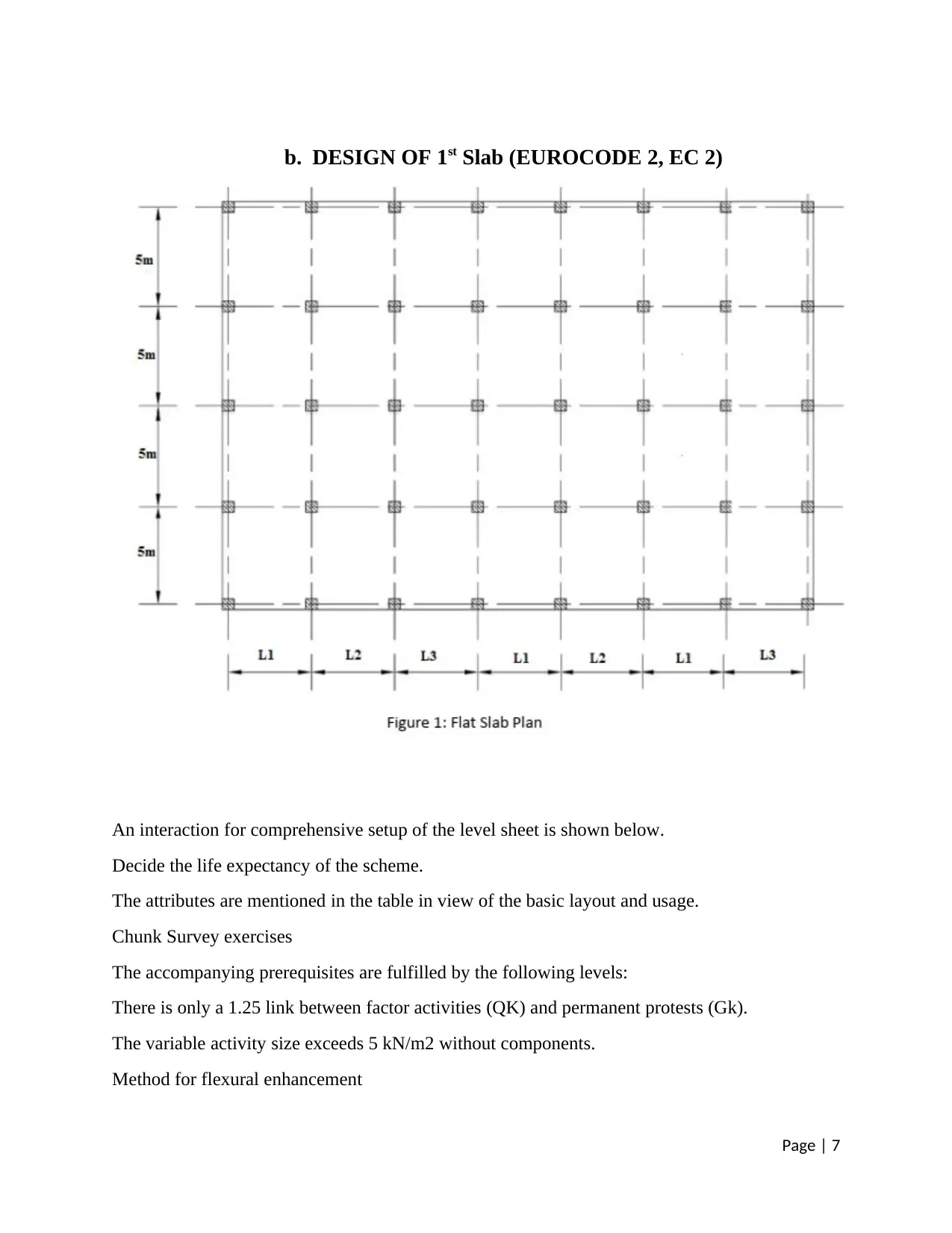
b. DESIGN OF 1st Slab (EUROCODE 2, EC 2)
An interaction for comprehensive setup of the level sheet is shown below.
Decide the life expectancy of the scheme.
The attributes are mentioned in the table in view of the basic layout and usage.
Chunk Survey exercises
The accompanying prerequisites are fulfilled by the following levels:
There is only a 1.25 link between factor activities (QK) and permanent protests (Gk).
The variable activity size exceeds 5 kN/m2 without components.
Method for flexural enhancement
Page | 7

Look at planning opening parts (M)
F is the definitive load of the scheme, whereas l represents the overriding burden.
This test is limited to significant class C5 0/60.
Find the solution to the problem K=M/bd2fck.
K'= 0.60 – 0.182 2 – 0.21 in which = 1.0% of d'or 0.60 – 0.182 2 – 0.21 (rearrangement
proportion) K' Fix the pressure in case of KK. There will be no support for pressure if this is not
the case.
Getting value of Z = d / 2 (1-3.53K) = 0.95 d.
Figure Pressure enhancement requirements for As=M/Fyd*z; requires minor upgrade track.
Fctm* d/FYK, Fyk=25, in, Fctm* d / Fyk, Fyk=25 Fctm*
Check for the most severe expansion prerequisites.
For stress or combination, max = 0.04 Ac outside lap regions.
Look at the evasion.
Eurocode 2 takes into account two types of diversion configuration: restricting range to depth
proportions or investigating hypothetical forwarding using Eurocode articulations. The ratio to
depth should be addressed. System for redirect detection. Calculate the l/d of the diagram below.
Page | 8

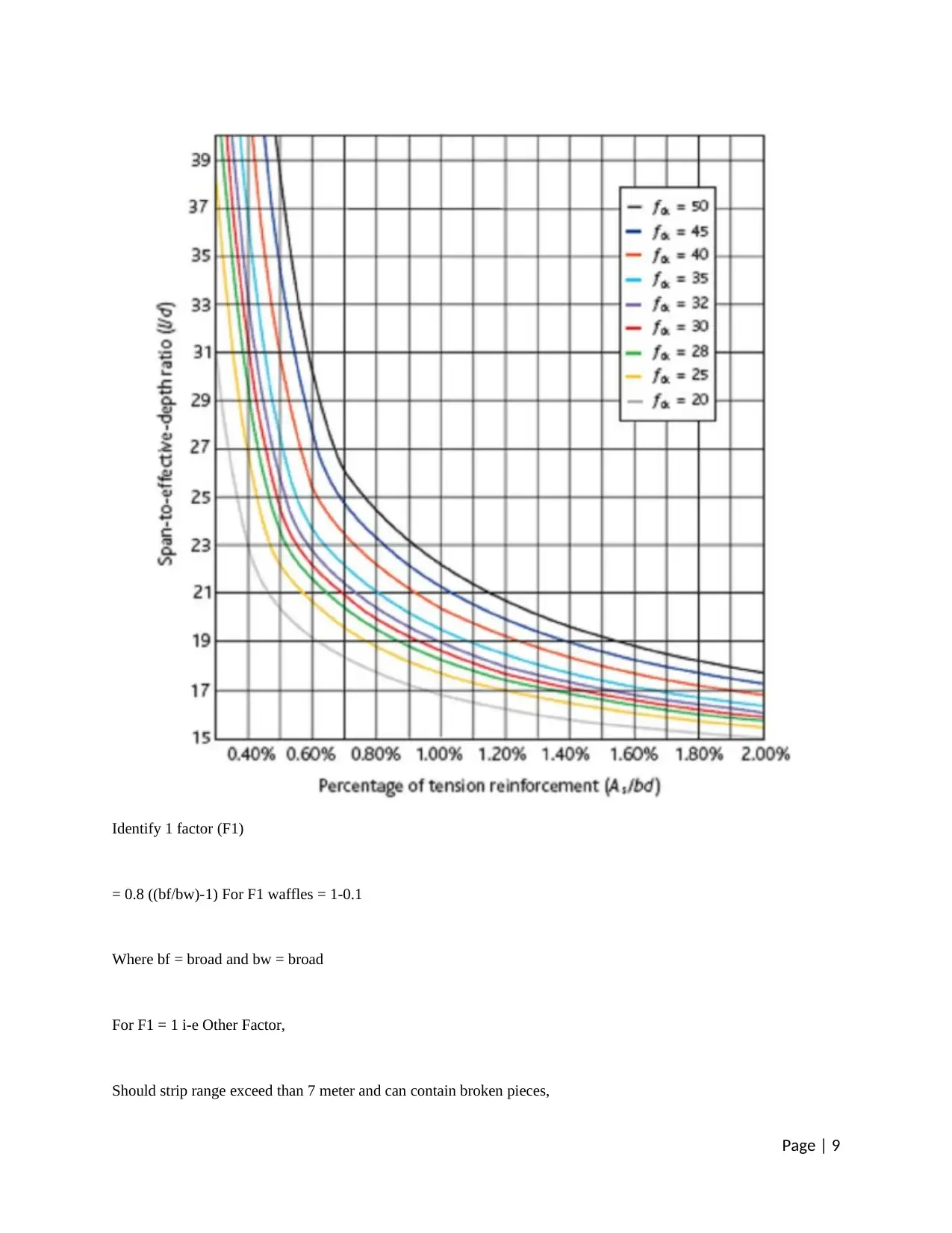
Identify 1 factor (F1)
= 0.8 ((bf/bw)-1) For F1 waffles = 1-0.1
Where bf = broad and bw = broad
For F1 = 1 i-e Other Factor,
Should strip range exceed than 7 meter and can contain broken pieces,
Page | 9

Thus, F2 = 7 /lef
Factor F2 = 1.0 Factor
Factor 3. F3: 310/s
Where
SS = functionality weight may be considered 290 MPa
(F3 = 1.0)
Essential l/d * F1 * F2 * F3 * Current l/d If this is achieved,
Then further we can calculate as
Shear's shots
Punching the plan appreciation of shear power, VEd, is usually the state support response.
Support should be in a spiral case. However, support might be extended to a matrix where divising requirements are
maintained.
Technique for assurance improvement
Choose factor β
Decide vEd esteem, the most severe shear configuration tension,
where ui is defined as = ( dy + dz ) / 2 segment edge
Decide vRd, Table 1 most extreme
If not adjust, check vEd,max vRd.
Identify vEd thisem (plan shear pressure)
VEd,max = β VEd/(ui deff) with length u1 border controls
Page | 10

In case it meets vEd > vRd,
c is called as Shear reinforcement which is not usually required
Borders of the Shear sponsor region:
Asw = (vEd – 0.75 vRd, c) sr u1 / (1.5 fywd, ef)
Where sr is the Fywd spiral distance,
Ef = 250 + 0.25
Decide which outer edge length is not required for shear support:
= VEd/Uut Uut (vRd,c d)
Check the distance of the bar
Mining or reinforcement
The base area in the main heading is As,
Min = 0.26 Fctm bt d/fyk but at least 0.0013b d.
We also know that foundation of the strength of the vertical punch shear is 1.5 As w,min/(sr.st)=0.08 fck 1⁄2 fyk.
Where sr = excess scattering association, st = distracting combination separating, F may be calculated or provided
Max region fortification
Max = 0.4 Ac should not reach outside lap spaces. Max = 0.4 Ac
Support for the last distance
The basis between bars should be:
Page | 11

Bar width + 20 mm.
Max support distance
The largest dispersion restrictions apply to plates less than 200 mm in thickness:
3h but not more than 400 mm for large support
For support: 3.5h, but not in excess of 450 mm.
The exclusion must apply where concentrated loads or very rapid regions apply:
There is 2 hors but not more than 250mm momentous support
Also for 3h but not in excess of 400 mm for support
Somewhere is the depth of the segment?
Section Calculation as specified by EC 2, Now the plate might be measured for 5 m longer as per the
aforementioned requirements.
More than 5.0 m long
Live load=6.5 kN/m2
Given significant assessment C20/25, e.g. fck=30 MPa
If C20/25 is to be 25 MPa for the chambers and C20/25 to be 20 MPa for the 3D square, chunk depth = range/21
(this depends on longer range)
Depth of effectiveness=314mm
Page | 12

Load calculations
Dead loading piece = 0,35 x 25 = 8,75 kN/m2 = wd
Load piece = 6.5 kN/m2 = wl
The Live Load Design should not exceed 1.25 Dead Load instances.
= 0.0885 < 1.25 Accompanying check: (safe)
All load out = 15.25 kN/m2
C20/25 = 29 kN/mm2 Secant versatility esteems
Longer period. Longer time.
Calculate K=M /bd2fck = 0.0129 K' = 0.60 ßen–0.182 β2–0.21, β= 1.0, = 0.1975 < K. (ok).
There is no pressure support needed.
Calculated = 0.95 Calculation of Z=d/2(1-3) .53K)
Alright,
Estimates of shears
Consider β= 1.15\svEd,max=β VEd/(ui deff)\swhere ui is perimeter=2000mm segment.
500x500 mm vEd,max=(1.15*896).
max=3.31 VRd ( from code)
Utopian VEd,max,max (safe)
= ß VEd = 1.16*896*103(1200*314) = 2.73 vRd, c =.75 vRd.
VEd > vRd,c All right.
Asw=(vEd – 0.75vRd,c)sr u1/ Shear support region (1.5 fywd).
Min area or support Min diameter=0,26 fctm d/fyk:=408,2mm2: Min area or support
As area of support, max=0.4 Ac=2415.5 mm2
Support for the last distance
The basis between bars should be:
Diameter of bar=12mm +5 mm = 9.75 mm
Twenty meters
Page | 13

Minute distance = 20mm
Max support distance
Use 12 mm bar = 4209 38 No.
Extreme distance = 36 mm No shear cage repair, no distance.
DESIGN OF 2nd Slab (EUROCODE 2, EC 2)
Identify 1 factor (F1)
= 0.9 ((bf/bw)-1) For F1 waffles = 1-0.1 = 0.9
Where bf = broad and bw = broad
For F1 = 1 i-e Other Factor,
Should strip range exceed than 7 meter and can contain broken pieces,
Thus, F2 = 7 /lef
Factor F2 = 1.0 Factor
Factor 3. F3: 325/s
Where
SS = functionality weight may be considered 290 MPa
(F3 = 1.25)
Then further we can calculate as
Shear's shots
Punching the plan appreciation of shear power, VEd, is usually the state support response.
Support should be in a spiral case. However, support might be extended to a matrix where divising requirements are
maintained.
Page | 14

Technique for assurance improvement
Choose factor β
Decide vEd esteem, the most severe shear configuration tension,
where ui is defined as = ( dx + dy + dz ) / 3 segment edge
Decide vRd, Table 1 most extreme
If not adjust, check vEd,max vRd.
Identify vEd thisem (plan shear pressure)
VEd,max = β VEd/(ui deff) with length u1 border controls
In case it meets vEd > vRd,
c is called as Shear reinforcement which is not usually required
Borders of the Shear sponsor region:
Asw = (vEd – 0.80 vRd, c) sr u1 / (1.85 fywd, ef)
Where sr is the Fywd spiral distance,
Ef = 270 + 0.50 = 270.5
Decide which outer edge length is not required for shear support:
= VEd/Uut Uut (vRd,c d)
Check the distance of the bar
Mining or reinforcement
The base area in the main heading is As,
Min = 0.28 Fctm bt d/fyk but at least 0.0011b d.
We also know that foundation of the strength of the vertical punch shear is 1.75 As w,min/(sr.st)=0.09 fck 1⁄2 fyk.
Page | 15

Where sr = excess scattering association, st = distracting combination separating, F may be calculated or provided
Max region fortification
Max = 0.4 Ac should not reach outside lap spaces. Max = 0.4 Ac
Support for the last distance
The basis between bars should be:
Bar width + 20 mm.
Max support distance
The largest dispersion restrictions apply to plates less than 200 mm in thickness:
3h but not more than 400 mm for large support
For support: 3.5h, but not in excess of 450 mm.
The exclusion must apply where concentrated loads or very rapid regions apply:
There is 2 hors but not more than 250mm momentous support
Also for 3h but not in excess of 400 mm for support
Somewhere is the depth of the segment?
Section Calculation as specified by EC 2, Now the plate might be measured for 5 m longer as per the
aforementioned requirements.
More than 5.0 m long
Live load=6.5 kN/m2
Page | 16

Given significant assessment C20/25, e.g. fck=30 MPa
If C20/25 is to be 25 MPa for the chambers and C20/25 to be 20 MPa for the 3D square, chunk depth = range/21
(this depends on longer range)
Depth of effectiveness=314mm
Load calculations
Dead loading piece = 0,35 x 25 = 8,75 kN/m2 = wd
Load piece = 6.5 kN/m2 = wl
The Live Load Design should not exceed 1.25 Dead Load instances.
= 0.0885 < 1.25 Accompanying check: (safe)
All load out = 16.36 kN/m2
C20/25 = 31.5 kN/mm2 Secant versatility esteems
Longer period. Longer time.
Calculate K=M /bd2fck = 0.0129 K' = 0.65 ß – 0.195 β2 – 0.25, β = 1.0, = 0.1865 < K. (ok).
There is no pressure support needed.
Calculated = 0.75 Calculation of Z=d/2(1-3) .53K)
Alright,
Min area or support Min diameter=0.28 fctm d/fyk:=408.2 mm
2: Min area or support
As area of support, max=0.5
Ac=2415.5 mm2
Support for the last distance
The basis between bars should be:
Diameter of bar=12mm +5 mm = 9.75 mm
Twenty meters
Page | 17

Minute distance = 20mm
Max support distance
Use 12 mm bar = 4186 38 No.
Extreme distance = 37.5 mm No shear cage repair, no distance.
c. Interior Column Designing
Interior Column can be easily designed using the following steps as per EC 2
1. Slenderness
Operative Lengths = Iol = Factor x I
Thus using the tables
We have the following values as
= 0.83
Now
I = Height = 3655 m
Now Iol = 0.83 x 3655 = 3033 mm
Now
Slenderness can be further calculated as, Sel = Iol/I * h/12^0.5 = 3033 * (3.32/300) =
33.58
2. Moments Designing
MEd = max [ M0Ed + M1Ed + 0.5M]
Now we can calculate further as
Page | 18

M0Ed = 0.8M02 + 0.5M01 ≥ 0.3M02
= 0.8 × 52.3 + 0.3 × (-36.5 + 11.9) ≥ 0.3 × 52.3
= 34.46 ≥ 15.69
= 34.46
Thus we can further check that calculated M2 = 0
From above result we can evaluate that the said column is not slender
M01 = M02
= max[M0Ed + M1Ed + 0.5M] = 51.4 kNm = MEd = 51.4 kNm
3. Using Chart and designing the said things
D2 = 49
D2 / h = 49 / 300 = 0.163
From interpolation we can get
0.15 and 0.20
4. Checking for Biaxial bending
(MEz/MRz) a + (MEy/MRy) a = (36.5/75.3)1.38 + (31.5/75.3)1.38
= 0.66 + 0.577
= 1.23
Thus it shows it’s all correct
5. Links
Diameter of the column can be calculated as = σ / 4 = 28 / 4 = 7 mm
Further Maximum Spacing = 0.7 x 300 = 210 mm
6. Summary of the Designed Column
fck = 30 MPa
Links @ 200 mm
4 H25
d. Analysis of the behavior of the exterior column and showing the result
thus reinforcement in under consideration two processes
Page | 19

Under unsaturated air conditions, concrete shrinkage is defined as a loss of volume caused by
moisture evaporation from concrete gel pores without any applied tension. While the majority of
compressive deformations occur in a short period of time (due to water drainage in capillary
holes caused by hydration of previously non-hydrous cement), shrinkage occurs throughout the
structure's service life, although at a considerably slower rate. All factors that influence concrete
shrinkage include temperature, humidity, time, design, material quality, treatment processes, and
specimen form. The limit of the shrinking processes generated by the components causes
compression and the building of tensile stresses in the surrounding concrete (reinforcement bars
in the case of RC constructions). The constant drop in an area is exacerbated by the uneven
moisture distribution. The emergence of the tensile creep phenomenon, on the other hand,
relieves the concrete's tensile tension.
The latter is defined as the gradual slow deformation of a material under continuous mechanical
stress (such as that caused by concrete shrinkage), which in our case results in the concrete
relaxing. The effect of creep on shrinkage is proportional to the size of the member, and it may
be negligible for small sections (as shown in the current article).
The consequences of controlled shrinkage should be carefully considered while designing an RC
structure. First, retention issues include a reduction in concrete's tensile capacity and, as a result,
a reduction in the structure's cracking load. Second, if the tensile strength of concrete is
surpassed, it will begin to fracture, resulting in reinforcement corrosion when the former happens
in a hostile and chemically hostile environment. The structure's durability and serviceability
would certainly suffer as a result of this. Finally, it was revealed that the structure's potential
tension pool is negatively impacted by the shrinkage.
As previously predicted, ignoring shrinkage effects in an RC member response results in a
perceived drop in concrete cracking strength as well as an influence on the strengthening ratio's
tension intensification. In reality, when the reinforcing percentage increases, the seeming
decrease of tension increases as well (becoming unneglectable beyond 1 percent). After the
shrinkage effect is removed, the tension stiffening seems to be independent of the reinforcing
rate. For all of the reasons stated above, tension intensification must be evaluated independently
of shrinkage's influence.
Page | 20

The effects of long-term shrinkage on the tensile behavior of 14 tested RC traction components,
particularly tension intensification, were investigated in this project. The major goal of this
project is to conduct a thorough analysis of concrete shrinkage and eliminate its causes. The
following findings were reached after reviewing the experimentally acquired data in line with the
EC2 and MC2010:
The cumulative decreasing strain of more than 5 years was significant enough to affect the
member's load de-formative behavior and stress-reinforcement behavior.
The RC part's apparent cracking load was reduced due to the shrinking effect.
The MC2010 model's projections were somewhat more accurate in terms of the raw test result,
whereas the EC2 model's projections were pretty accurate in terms of tension stiffening.
Discussion
The fibre-reforced concrete (FRC), i.e. concrete made with steel or polymer fibres that may
provide significant technological and economic advantages, has been one of the most promising
forms of concrete for both structural and non-structural applications in recent decades. Studies
employing multi-criteria decision-making approaches taking into account social, environmental
and economic sustainability have indicated as well that for different infrastructure projects where
fibre use is technically practicable, FRC may be sustainable than reinforced concrete (RC) (as
unique reinforcement or in combination with traditional steel rebars). Given the vast quantities of
global concrete, i.e. more than 25 billion tonnes, this development towards more sustainable
alternatives is crucial. Almost 50% of the total manufactured concrete is used in structural
applications in industrialised countries The FRC has therefore increasingly been tested as a
solution to replace partial or even complete reinforcement for applications such as ground-based
slabs, floors, roads, tunnel lines, pipe sewage lines and flat slabs which means it is used more
and more in elements exposed to bending, long-term gravitational resistence. Over recent years,
FRC structural design has been included in several design codes, such as the 2010, ACI 318,
Page | 21

Italian and Spanish Code, thanks to a significant research. However, until now, research has
focused on short-term material and structural properties, leaving other FRC design challenges in
the early stages of research. One such feature is the time-sensitive behaviour of FRC, in
particular its creep. Even without considering the effects of fibre, the mechanical behaviour of
RC structures is tough to assess because of issues including shrinkage, cracking and cracking.
FRC introduces extra complexity, in particular since it is possible for the FRC itself to be built
with several types of fibres, such as steel fibre (SFRC) or polymer fibres (PFRC), which have a
variety of mechanical features. Overall, it is important to evaluate the progression of fiber-matrix
interface creep or damage, as well as the debonding and tugging of fibres and the sensitivity of
fibre filaments to tensile creeps in certain polymer fibre when exposed to stresses incompatible
with material characteristics. In conjunction with a creep and concrete recession, the FRC
members may be prone to increasing crack widths and therefore likely loss of functionality,
durability and ultimately mechanical performance. Fracture width is a steel-based reinforcing
control parameter for concrete and thorough experiments have shown that chloride-induced
corrosion and break-up processes are sensitive to fracture width. The use of polymer-based
compounds as concrete reinforcements is unexpected. However, polymeric fibres creeping in
cracked portions might lead to mechanical capacity losses if they undergo persistent loads of
magnitudes that are incompatible with fiber's time-related mechanical characteristics. This
disadvantage may be alleviated by hybrid technologies (fibre and steel reinforcement bars,
"hybrid-FRC")[26]. It is so evident that cracking fractured FRC elements have considerable
design and structural implications and should be properly assessed. Although there are some
fundamental needs and recommendations, due to a lack of consistent research (extremely limited
and limited), reliable design and serviceability limit status (SLS) calculation approaches for
analysing the cracked FRC structures subjected to long-term bending still need.
In unsaturated air circumstances, concrete shrinkage is defined as volume loss from concrete gel
pores without applied tension, induced by moisture evaporation. But most compressive
deformations occur within a short time (because of water drainage in capillary holes generated
by hydration of previously unhydrous cement), they are reversed over the life of the structure,
although at a reduced pace. Temperature, humidity, time, design, material quality, treatment
procedures and the shape of the specimen all impact concrete shrinking. The limitation of the
shrinking processes produced by the components creates tensile strains and compression in the
Page | 22

surrounding concrete (reinforcement bars in the case of RC constructions). The continuous
decline in a region is compounded by the unequal distribution of moisture. On the other side, the
formation of the tensile creep phenomena relieves the tensile stress of the concrete.
The latter is described as the progressive deformation, which leads to a concrete relaxation of a
material with continuous mechanical stress (such as the one induced by concrete shrinkage). The
impact of creep is related to the member's size and may be minimal in tiny parts (as shown in the
current article).
The ramifications of controlled reduction during the design of the RC structure should be
carefully studied. First, the problems of retention include reducing the tensile capacity of the
concrete and thereby reducing the structure's cracking load. Secondly, if the tensile strength of
the concrete is exceeded, the fracture begins and reinforcement corrosion occurs when the former
occurs in a hostile and chemical environment. The longevity and serviceability of the structure
would surely be affected as a consequence. Finally, it was shown that the potential tension pool
of the structure is adversely affected by the shrinking.
As previously forecast, disregarding the shrinkage effects of an RC member reaction leads to a
perceived decrease in concrete cracking strength and to an impact on the tension intensification
ratio. In fact, the apparent reduction in tension grows as the strengthening percentage rises
(becoming unneglectable beyond 1 percent). After the shrinking effect has been eliminated, the
stress intensification seems to be independent of the reinforcement rate. For all the foregoing
reasons, tension intensification must be assessed regardless of the effects of decline.
Conclusion and Recommendation.
The load calculation and designing of Slabs, Flat Slab and Column is discussed in this
assignment using EC 2. Furthermore, shrinkage and creep of RPC is also examined to some
extent. The effects of the axial stress ratio on creep, as well as the impact of steel fiber on
shrinkage and creep, were addressed. The experimental findings were then analysed and checked
as well using the standards of Euro-code 2, because of its thick microstructure, RPC has a greater
compressive strength than regular strength concrete. The modulus elastic and compressive
Page | 23

strength improve as the steel fiber content increases, since the steel fiber prevents micro cracks
and transverse deformation. Because of the enhanced homogeneity and decreased pore size, RPC
shrinks substantially less than regular strength concrete. Due to the micro-scale water films
generated on the steel fiber surface and the skeleton produced by the cross and overlap of steel
fiber, shrinkage reduces as steel fiber content increases. The creep of RPC reduces as the steel
fiber content increases, which is noticeable in the latter stages following loading because steel
fiber may inhibit the formation of micro cracks (which appear mostly in the latter stages).
Furthermore, the slip between the steel fiber and the RPC matrix tends to remain constant over
time, and the steel fiber's capacity to suppress creep gradually emerges. The creep strain of RPC
changes linearly with the axial stress ratio for axial stress ratios smaller than 0.4. (RPC is in the
linear creep stage). Furthermore, all four models overestimate RPC's creep strain. As a result,
these models can't be utilised to anticipate RPC shrinkage and creep. Simple shrinkage and creep
models for RPC have been devised, taking into account the effects of steel fiber. The design of
the both slab and the columns shows that we can we have the main strengths and shows that
potential tension pool of the structure is adversely affected by the shrinking.
Page | 24

References
1. ZHANG, W.W.; Fu, B.J.; Meng, Q.H.; Zhang, Q.J.; Zhang, Y.H. Effects of land-use
pattern change on rainfall-runoff and runoff-sediment relations: A case study in Zichang
watershed of the Loess Plateau of China. J. Environ. Sci.2004, 16, 436–442.
2. Sakata, K. Prediction of Creep and Shrinkage of Concrete. Jpn. Soc. Civ. Eng. 1996,
160–171. 5. Collins, F.; Sanjayan, J.G. Effect of pore size distribution on drying
shrinkage of alkali-activated slag concrete. Cem. Concrete Res. 2000, 30, 1401–1406.
[CrossRef]
3. Barcelo, L.; Moranville, M.; Clavaud, B. Autogenous shrinkage of concrete: A balance
between autogenous swelling and self-desiccation. Cem. Concr. Res. 2005, 35, 177–183.
[CrossRef]
4. Aili, A.; Vandamme, M.; Torrenti, J.; Masson, B. Is long-term autogenous shrinkage a
creep phenomenon induced by capillary effects due to self-desiccation? Cem. Concr. Res.
2018, 108, 186–200. [CrossRef]
5. Holt, E. Contribution of mixture design to chemical and autogenous shrinkage of
concrete at early ages. Cem. Concr. Res. 2005, 35, 464–472. [CrossRef]
Page | 25

6. Seddik Meddah, M.; Tagnit-Hamou, A. Evaluation of rate of deformation for early-age
concrete shrinkage analysis and time zero determination. J. Mater. Civ. Eng. 2011, 23,
1076–1086. [CrossRef]
7. Jaafari, C.; Bertrand, D.; Guillot, T.; Prudhomme, E.; Tardif, N.; Georgin, J.F.;
Delhomme, F.; Trunfio, R.; Chateur, N.; Bruyere, E.; et al. Effect of early age drying
shrinkage on the seismic response of RC structures. Mater. Struct. 2020, 53. [CrossRef]
8. Yazdizadeh, Z.; Marzouk, H.; Hadianfard, M.A. Monitoring of concrete shrinkage and
creep using Fiber Bragg Grating sensors. Constr. Build. Mater. 2017, 137, 505–512.
[CrossRef]
9. Davis, M.B.; Hoult, N.A.; Bajaj, S.; Bentz, E.C. Distributed Sensing for Shrinkage and
Tension Stiffening Measurement. ACI Struct. J. 2017, 114. [CrossRef] 13. Han, B.;
Xiang, T.; Xie, H. A Bayesian inference framework for predicting the long-term
deflection of concrete structures caused by creep and shrinkage. Eng. Struct. 2017, 142,
46–55. [CrossRef]
10. Bazant, Z.P.; Osman, E.; Thonguthai, W. Practical formulation of shrinkage and creep of
concrete. Mater. Constr. 1976, 9, 395–406. [CrossRef]
11. Nguyen, D.H.; Dao, V.T.N.; Lura, P. Tensile properties of concrete at very early ages.
Constr. Build. Mater. 2017, 134, 563–573. [CrossRef] 16. Liu, J.; Yan, K.Z.; Zhao, X.;
Hu, Y. Prediction of autogenous shrinkage of concretes by support vector machine. Int. J.
Pavement Res. Technol. 2016, 9, 169–177. [CrossRef]
12. Goel, R.; Kumar, R.; Paul, D.K. Comparative study of various creep and shrinkage
prediction models for concrete. J. Mater. Civ. Eng. 2007, 19, 249–260. [CrossRef]
Page | 26