ITC544 Computer Architecture and Organization: Number Systems
VerifiedAdded on 2023/06/14
|9
|841
|314
Homework Assignment
AI Summary
This assignment solution focuses on computer architecture and organization, covering number system conversions and Boolean algebra. It begins with determining the base 'x' of a number given its hexadecimal equivalent. Various number conversions are performed, including converting BED16 to base-3, 3217 to binary, 1235 in decimal to octal, and 21.218 to decimal. The assignment then explores the representation of values using one's complement, two's complement, and signed magnitude. Finally, the assignment provides proofs of Boolean algebra expressions, including demonstrating De-Morgan's Law and minimizing logic circuits. Desklib offers a variety of solved assignments and past papers for students seeking assistance with their studies.

Running head: COMPUTER ARCHITECHTURE AND ORGANIZATION
Computer Architecture and Organization
Full name:
Student ID:
Subject Code: ITC544
Author’s Note
Computer Architecture and Organization
Full name:
Student ID:
Subject Code: ITC544
Author’s Note
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1
COMPUTER ARCHITECHTURE AND ORGANIZATION
Table of Contents
Question 1:.......................................................................................................................................2
a.) Determining the value of base x if (152) x = (6A) 16............................................................2
b) Conversions.............................................................................................................................2
c) Representation of value..........................................................................................................5
Question 2:.......................................................................................................................................5
a) Prove........................................................................................................................................5
b) Using basic Boolean algebra identities for Boolean variables x, y, and z, for prove..............7
c) Prove:......................................................................................................................................7
COMPUTER ARCHITECHTURE AND ORGANIZATION
Table of Contents
Question 1:.......................................................................................................................................2
a.) Determining the value of base x if (152) x = (6A) 16............................................................2
b) Conversions.............................................................................................................................2
c) Representation of value..........................................................................................................5
Question 2:.......................................................................................................................................5
a) Prove........................................................................................................................................5
b) Using basic Boolean algebra identities for Boolean variables x, y, and z, for prove..............7
c) Prove:......................................................................................................................................7

2
COMPUTER ARCHITECHTURE AND ORGANIZATION
Question 1:
a.) Determining the value of base x if (152) x = (6A) 16
Let the value of base be X,
Given,
(152) x = (6A) 16
Or, X^2 + 5X + 2*X = 6*16 + A
Or, X^2 + 5X + 2*X = 6*16 + 10
X2 + 5X + 2 = 106
X^2 + 5X- 104 = 0
X^2 + 13X- 8X – 104 = 0
X (X + 13) – 8(X + 13) = 0
(X - 8) (X + 13) = 0
X = 8 and X = -13
Hence, X is 8.
The value of the base is 8.
b) Conversions
i) BED16 converting to base-3
Solution:
COMPUTER ARCHITECHTURE AND ORGANIZATION
Question 1:
a.) Determining the value of base x if (152) x = (6A) 16
Let the value of base be X,
Given,
(152) x = (6A) 16
Or, X^2 + 5X + 2*X = 6*16 + A
Or, X^2 + 5X + 2*X = 6*16 + 10
X2 + 5X + 2 = 106
X^2 + 5X- 104 = 0
X^2 + 13X- 8X – 104 = 0
X (X + 13) – 8(X + 13) = 0
(X - 8) (X + 13) = 0
X = 8 and X = -13
Hence, X is 8.
The value of the base is 8.
b) Conversions
i) BED16 converting to base-3
Solution:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3
COMPUTER ARCHITECHTURE AND ORGANIZATION
= B * 16*16 + E * 16 + D
= 2816 + 224 + 13
= (3053)10
(3053)10 =
3 3053
3 1017 2
3 339 0
3 113 0
3 37 2
3 12 1
3 4 0
3 1 1
So, (BED)16 = (11012002)3
ii) 3217 into 2-base (binary) representation
Solution:
(321)7 = (3 * 72) + (2 * 71) + (1 * 70)
= (162)10
Again, (162)10 =
2 162
COMPUTER ARCHITECHTURE AND ORGANIZATION
= B * 16*16 + E * 16 + D
= 2816 + 224 + 13
= (3053)10
(3053)10 =
3 3053
3 1017 2
3 339 0
3 113 0
3 37 2
3 12 1
3 4 0
3 1 1
So, (BED)16 = (11012002)3
ii) 3217 into 2-base (binary) representation
Solution:
(321)7 = (3 * 72) + (2 * 71) + (1 * 70)
= (162)10
Again, (162)10 =
2 162
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

4
COMPUTER ARCHITECHTURE AND ORGANIZATION
2 81 0
2 40 1
2 20 0
2 10 0
2 5 0
2 2 1
2 1 0
Hence, (162)10 = (10100010)2
iii) (1235)10 conversion to octal representation
Solution:
8 1235
8 154 3
8 19 2
8 2 3
Hence, (1235)10 = (2323)8
iv) 21.218 conversion to decimal representation
Solution:
21.218 = (2 * 81) + (1 * 80). (2 * 8-1) + (1 * 7=8-2)
= 17 + 0.25 + 0.015625
COMPUTER ARCHITECHTURE AND ORGANIZATION
2 81 0
2 40 1
2 20 0
2 10 0
2 5 0
2 2 1
2 1 0
Hence, (162)10 = (10100010)2
iii) (1235)10 conversion to octal representation
Solution:
8 1235
8 154 3
8 19 2
8 2 3
Hence, (1235)10 = (2323)8
iv) 21.218 conversion to decimal representation
Solution:
21.218 = (2 * 81) + (1 * 80). (2 * 8-1) + (1 * 7=8-2)
= 17 + 0.25 + 0.015625

5
COMPUTER ARCHITECHTURE AND ORGANIZATION
= 17.265625
c) Representation of value
i) One's complement
Highest Value is 011
Lowest Value is 100
ii) Two's complement
Highest Value is 011
Lowest Value is 101
iii) Signed Magnitude
Highest Value is 011
Lowest Value is 111
Question 2:
a) Prove
The expression for the logic diagram is: (a.b)’
The Truth table of the above expression is provided below:
A b a.b (a.b)’
0 0 0 1
COMPUTER ARCHITECHTURE AND ORGANIZATION
= 17.265625
c) Representation of value
i) One's complement
Highest Value is 011
Lowest Value is 100
ii) Two's complement
Highest Value is 011
Lowest Value is 101
iii) Signed Magnitude
Highest Value is 011
Lowest Value is 111
Question 2:
a) Prove
The expression for the logic diagram is: (a.b)’
The Truth table of the above expression is provided below:
A b a.b (a.b)’
0 0 0 1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

6
COMPUTER ARCHITECHTURE AND ORGANIZATION
0 1 0 1
1 0 0 1
1 1 1 0
The expression of the logic diagram is provided below:
a’ + b’
The truth table for the above expression is provided below:
A b a’ b’ a’ + b’
0 0 1 1 1
0 1 1 0 1
1 0 0 1 1
1 1 0 0 0
Hence, LHS = RHS (Proved)
COMPUTER ARCHITECHTURE AND ORGANIZATION
0 1 0 1
1 0 0 1
1 1 1 0
The expression of the logic diagram is provided below:
a’ + b’
The truth table for the above expression is provided below:
A b a’ b’ a’ + b’
0 0 1 1 1
0 1 1 0 1
1 0 0 1 1
1 1 0 0 0
Hence, LHS = RHS (Proved)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
7
COMPUTER ARCHITECHTURE AND ORGANIZATION
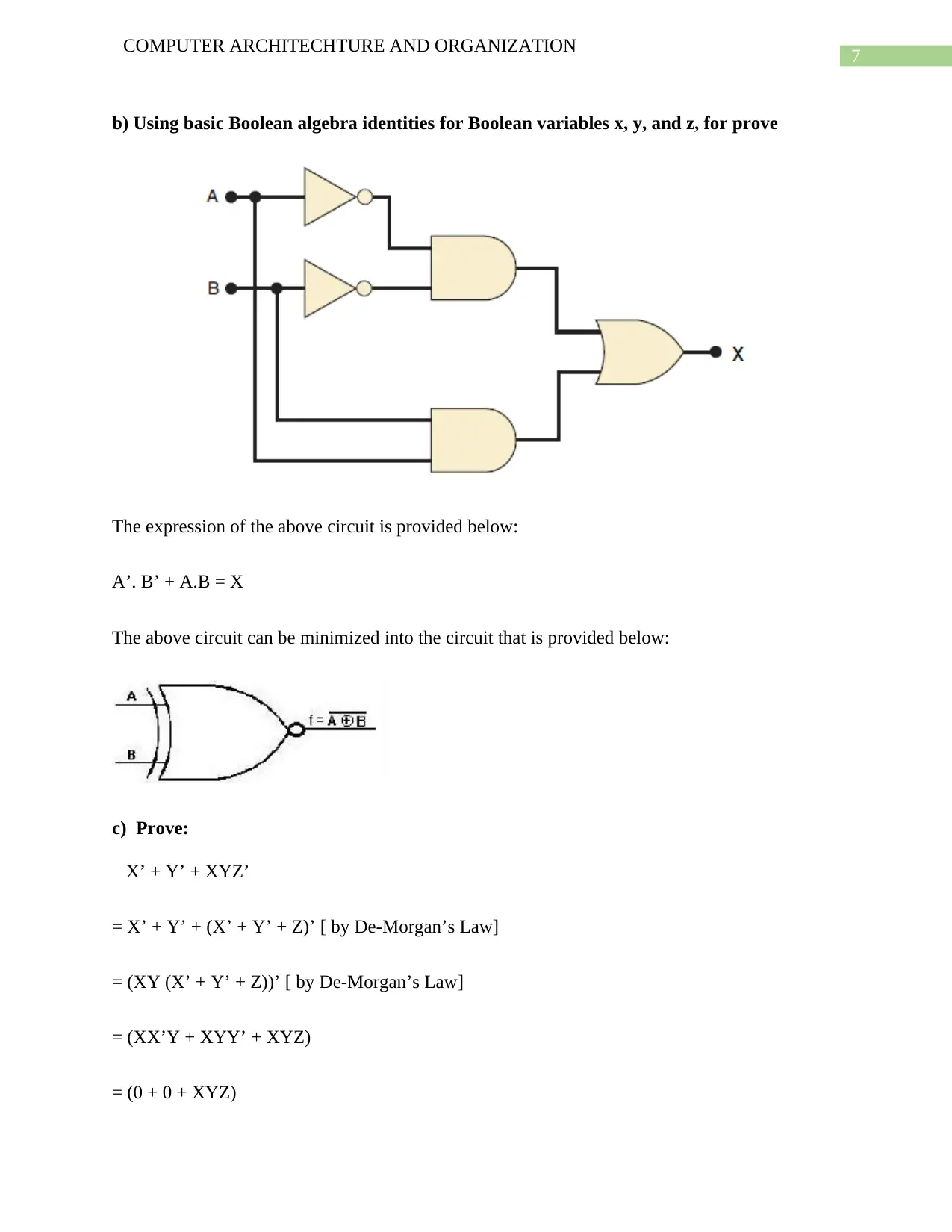
b) Using basic Boolean algebra identities for Boolean variables x, y, and z, for prove
The expression of the above circuit is provided below:
A’. B’ + A.B = X
The above circuit can be minimized into the circuit that is provided below:
c) Prove:
X’ + Y’ + XYZ’
= X’ + Y’ + (X’ + Y’ + Z)’ [ by De-Morgan’s Law]
= (XY (X’ + Y’ + Z))’ [ by De-Morgan’s Law]
= (XX’Y + XYY’ + XYZ)
= (0 + 0 + XYZ)
COMPUTER ARCHITECHTURE AND ORGANIZATION
b) Using basic Boolean algebra identities for Boolean variables x, y, and z, for prove
The expression of the above circuit is provided below:
A’. B’ + A.B = X
The above circuit can be minimized into the circuit that is provided below:
c) Prove:
X’ + Y’ + XYZ’
= X’ + Y’ + (X’ + Y’ + Z)’ [ by De-Morgan’s Law]
= (XY (X’ + Y’ + Z))’ [ by De-Morgan’s Law]
= (XX’Y + XYY’ + XYZ)
= (0 + 0 + XYZ)

8
COMPUTER ARCHITECHTURE AND ORGANIZATION
= (XYZ)’
= X’ + Y’ + Z’ [ by De-Morgan’s Law]
Hence, X’ + Y’ + XYZ’ = X’ + Y’ + Z’ [PROVED]
COMPUTER ARCHITECHTURE AND ORGANIZATION
= (XYZ)’
= X’ + Y’ + Z’ [ by De-Morgan’s Law]
Hence, X’ + Y’ + XYZ’ = X’ + Y’ + Z’ [PROVED]
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.


