ITC544 Assignment Solution: Computer Architecture and Organization

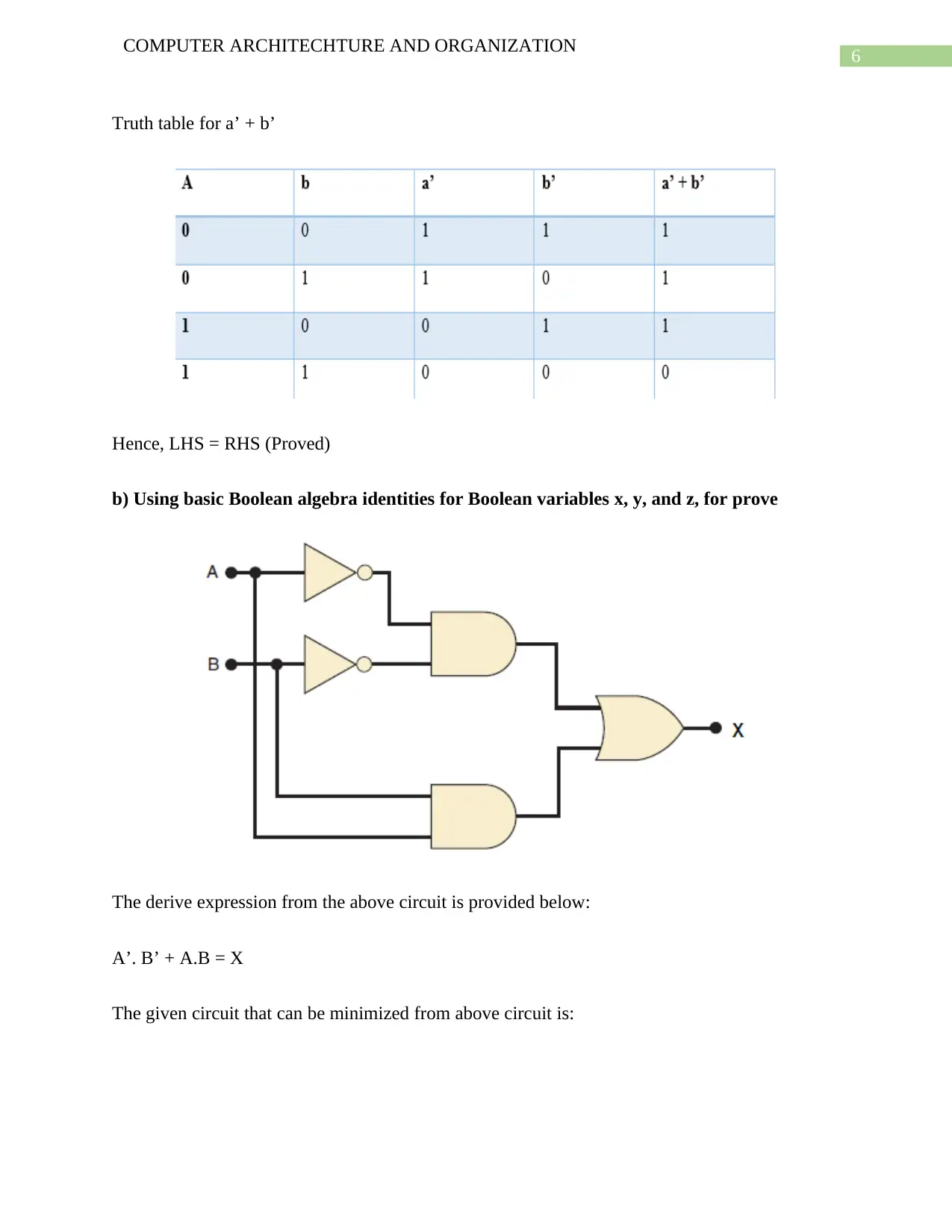
This document presents a detailed solution to a Computer Architecture and Organization assignment, specifically for the course ITC544. The assignment covers topics such as number base conversions, including converting between base-16, base-3, base-7, base-10, and binary representations. It also explores 1's complement, 2's complement, and signed magnitude representations, determining the highest and lowest values for each. Furthermore, the solution includes proofs using Boolean algebra identities and De-Morgan's Law, along with analysis and minimization of logic circuits. Desklib offers this assignment solution as part of its collection of solved assignments and study resources to aid students in their learning.

Running head: COMPUTER ARCHITECHTURE AND ORGANIZATION
Computer Architecture and Organization
Full name:
Student ID:
Subject Code: ITC544
Author’s Note

1
COMPUTER ARCHITECHTURE AND ORGANIZATION
Table of Contents
Question 1:.......................................................................................................................................2
a.) Determining the value of base x if (152) x = (6A) 16............................................................2
b) Conversions.............................................................................................................................2
c) Representation of value..........................................................................................................5
Question 2:.......................................................................................................................................5
a) Prove........................................................................................................................................5
b) Using basic Boolean algebra identities for Boolean variables x, y, and z, for prove..............7
c) Prove:......................................................................................................................................7

2
COMPUTER ARCHITECHTURE AND ORGANIZATION
Answer to Question 1:
A.) Value of base x if (152) x = (6A) 16
The value of base is considered as X
Provided:
(152) x = (6A) 16
Or, X^2 + 5X + 2*X = 6*16 + A
Or, X^2 + 5X + 2*X = 6*16 + 10
X^2 + 5X + 2 = 106
X^2 + 5X- 104 = 0
X^2 + 13X- 8X – 104 = 0
X (X + 13) – 8(X + 13) = 0
(X - 8) (X + 13) = 0
X = 8 and X = -13
Therefore the value of X is 8.
b) Conversions
i) BED16 converting to base-3
= B * 16*16 + E * 16 + D
= 2816 + 224 + 13
= (3053)10

3
COMPUTER ARCHITECHTURE AND ORGANIZATION
(3053)10 =
Therefore,(BED)16 = (11012002)3
ii) 3217 into 2-base (binary) representation
(321)7 = (3 * 72) + (2 * 71) + (1 * 70)
= (162)10
Again, (162)10 =

4
COMPUTER ARCHITECHTURE AND ORGANIZATION
Hence, (162)10 = (10100010)2
iii) (1235)10 conversion to octal representation
Solution:
Therefore, (1235)10 = (2323)8
iv) 21.218 conversion to decimal representation
21.218 = (2 * 81) + (1 * 80). (2 * 8-1) + (1 * 7=8-2)
= 17 + 0.25 + 0.015625
= 17.265625
c) Representation of value
i) Highest and lowest value for 1’s complement
Highest Value is 011
Lowest Value is 100
ii) Highest and lowest value for 1’s complement
Highest Value is 011
Lowest Value is 101
iii) Highest and lowest value signed Magnitude

5
COMPUTER ARCHITECHTURE AND ORGANIZATION
Highest Value is 011
Lowest Value is 111
Question 2:
a) Prove
The expression for the above logic diagram is: (a.b)’
Truth table for (a.b)’
The expression of the logic diagram
a’ + b’

6
COMPUTER ARCHITECHTURE AND ORGANIZATION
Truth table for a’ + b’
Hence, LHS = RHS (Proved)
b) Using basic Boolean algebra identities for Boolean variables x, y, and z, for prove
The derive expression from the above circuit is provided below:
A’. B’ + A.B = X
The given circuit that can be minimized from above circuit is:

7
COMPUTER ARCHITECHTURE AND ORGANIZATION
c) Prove:
X’ + Y’ + XYZ’
= X’ + Y’ + (X’ + Y’ + Z)’ [by using De-Morgan’s Law]
= (XY (X’ + Y’ + Z))’ [by using De-Morgan’s Law]
= (XX’Y + XYY’ + XYZ)
= (0 + 0 + XYZ)
= (XYZ)’
= X’ + Y’ + Z’ [by using De-Morgan’s Law]
Therefore, X’ + Y’ + XYZ’ = X’ + Y’ + Z’ [PROVED]