Exploring Data Representation & Digital Logic in Architecture

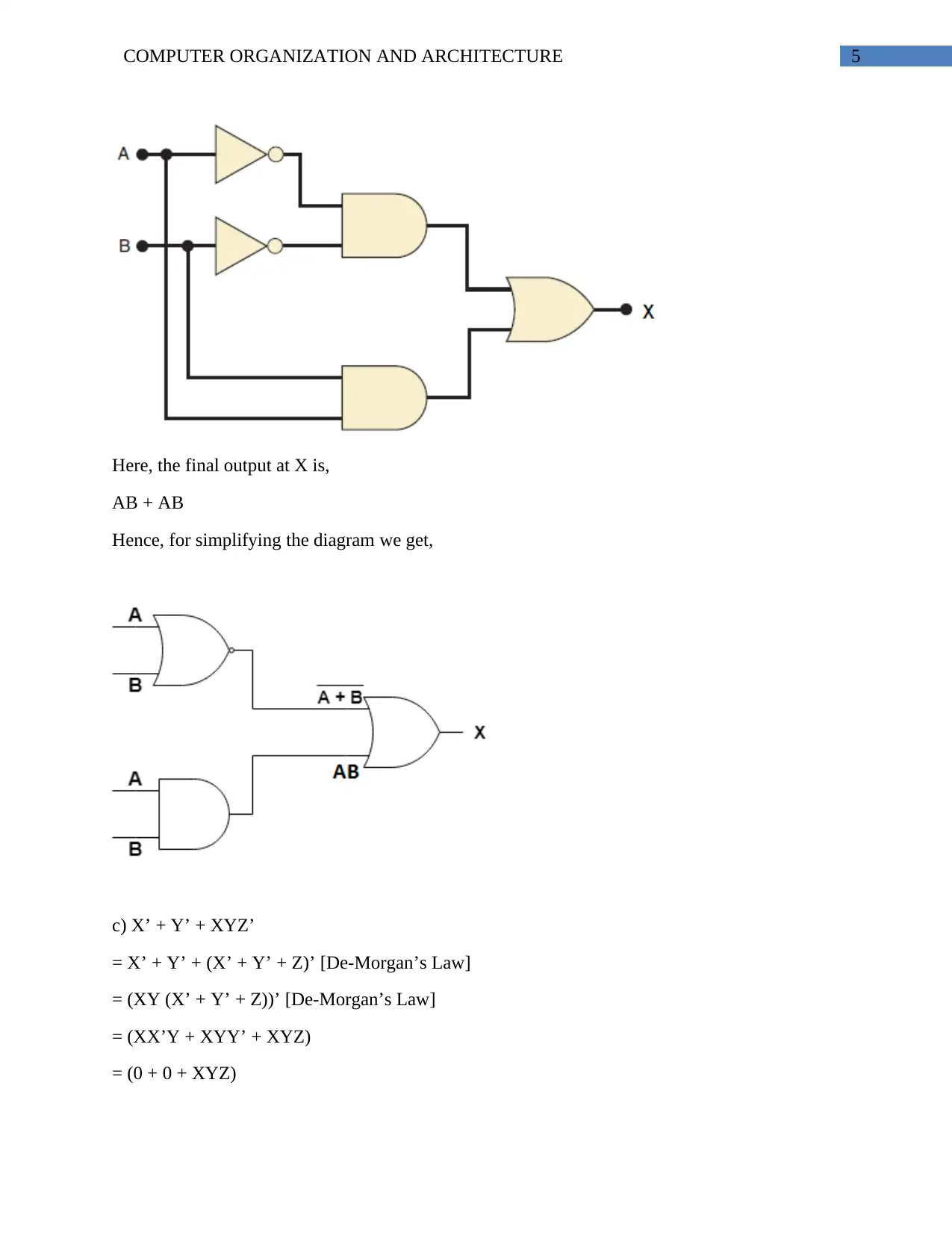
This assignment focuses on data representation and digital logic within the context of computer organization and architecture. It includes problems related to base conversion, such as converting between hexadecimal, base-3, base-2, octal, and decimal representations. The assignment also explores the limitations of a tiny computer with a 3-bit word size, examining the lowest and highest values it can represent using one's complement, two's complement, and signed magnitude representations. Furthermore, it delves into digital logic, verifying the equivalence of logic circuits and simplifying Boolean expressions using De-Morgan's Law. This solved assignment provides comprehensive solutions and explanations, aiding students in understanding key concepts in computer architecture. Desklib offers a wealth of similar resources and past papers to support student learning.

Running head: COMPUTER ORGANIZATION AND ARCHITECTURE
Assignment 1: Data Representation and Digital Logic
Name of the Student:
Student ID:
Name of the University:
Author’s note:

1COMPUTER ORGANIZATION AND ARCHITECTURE
Question 1
a. Determine the value of base x if (152)x = (6A)16
Solution:
Given,
(152) x= (6A) 16
LHS,
(152) x
= X2 + (5 * X1) + (2 * X0)
= X2 + 5X + 2
RHS,
(6A) 16
= (6 * 161) + (10 * 160)
= 106
Since, LHS=RHS. Therefore,
X2 + 5X + 2=106
=) X2 + 5X - 104 = 0
=) X2 + 13X - 8X – 104 = 0
=) X(X + 13) – 8(X + 13) = 0
=) (X - 8) (X + 13) = 0
Therefore,
Either X=8 or -13
Since, X is a base and hence it cannot be in negative power. Therefore the final solution for X is
8.
Answer: The value of X is 8 for (152)x = (6A)16
b) Convert the followings:
i. BED16 into 3-base representation

2COMPUTER ORGANIZATION AND ARCHITECTURE
For converting BED16 into base 3, first we need to convert it into decimal form,
BED16
= (B * 162) + (E * 161) + (D * 160)
= 2816 + 224 + 13
= (3053)10
Now, 305310=
Divisor Dividend Remainder
3 3053 2
3 1017 0
3 339 0
3 113 2
3 37 1
3 12 0
3 4 1
1
Therefore, (BED)16 = (11012002)3
ii) 3217 conversion to base-2
For converting 3217 into base 2, first we need to convert it into decimal form,
(321)7
= (3 * 72) + (2 * 71) + (1 * 70)
= (162)10
Now, (162)10=
Divisor Dividend Remainder
2 162 0
2 81 1
2 40 0
2 20 0
2 10 0
2 5 1
2 2 0
1
Therefore, (321)7= (10100010)2
iii) (1235)10 conversion to octal representation

3COMPUTER ORGANIZATION AND ARCHITECTURE
(1235)10 =
Divisor Dividend Remainder
8 1235 3
8 154 2
8 19 3
2
Therefore, (1235)10 = (2323)8
iv) 21.218 conversion to decimal representation
21.218
= (2 * 81) + (1 * 80). (2 * 8-1) + (1 * 7=8-2)
= 17 + 0.25 + 0.015625
= 17.265625
Therefore,
21.218= 17.26562510
c) Given a (very) tiny computer that has a word size of 3 bits, what are the lowest value (negative
number) and the highest value (positive number) that this computer can represent in each of the
following representations?
i) One's complement
ii) Two's complement
iii) Signed Magnitude
Answer:
For a computer size of 3 bit,
Highest Lowest
One's complement 011 100
Two's complement 011 101
Signed Magnitude 011 111
Question 2
a) From the given question, output of L.H.S is

4COMPUTER ORGANIZATION AND ARCHITECTURE
a 0 0 1 1
b 0 1 0 1
c 0 0 0 1
d 1 1 1 0
From the given R.H.S., the output of the circuit is
a 0 0 1 1
b 0 1 0 1
c 1 1 0 1
d 1 0 1 0
e 1 1 1 0
Therefore, the output of given L.H.S. is same as the output of the given R.H.S.
b) The given circuit is:

5COMPUTER ORGANIZATION AND ARCHITECTURE
Here, the final output at X is,
AB + AB
Hence, for simplifying the diagram we get,
c) X’ + Y’ + XYZ’
= X’ + Y’ + (X’ + Y’ + Z)’ [De-Morgan’s Law]
= (XY (X’ + Y’ + Z))’ [De-Morgan’s Law]
= (XX’Y + XYY’ + XYZ)
= (0 + 0 + XYZ)

6COMPUTER ORGANIZATION AND ARCHITECTURE
= (XYZ)’
= X’ + Y’ + Z’ [De-Morgan’s Law]
Hence, X’ + Y’ + XYZ’ = X’ + Y’ + Z’ [PROVED]

7COMPUTER ORGANIZATION AND ARCHITECTURE
Bibliography
Harris, S., & Harris, D. (2015). Digital Design and Computer Architecture: ARM Edition.
Morgan Kaufmann.
Jaeger, R. C., & Blalock, T. N. (2015). Microelectronic circuit design. McGraw-Hill
Science/Engineering/Math.
Martí-Campoy, A., Petit, S., Atienza, V., Rodríguez, F., & Gassó, M. T. (2014, June). Using
peer-assessed returnables in multiple stages to improve learning in computer organization
courses. In Tecnologias Aplicadas a la Ensenanza de la Electronica (Technologies
Applied to Electronics Teaching)(TAEE), 2014 XI (pp. 1-6). IEEE.
Prinz, P., Crawford, T., Hennessy, J. L., & Patterson, D. A. (2018). Computer Architecture: A
Quantitative Approach.
Siewiorek, D., & Swarz, R. (2017). Reliable Computer Systems: Design and Evaluatuion. Digital
Press.
Tolpygo, S. K. (2016). Superconductor digital electronics: Scalability and energy efficiency
issues. Low Temperature Physics, 42(5), 361-379.