Computer Organization Assignment: Base Conversion and Logic Gates

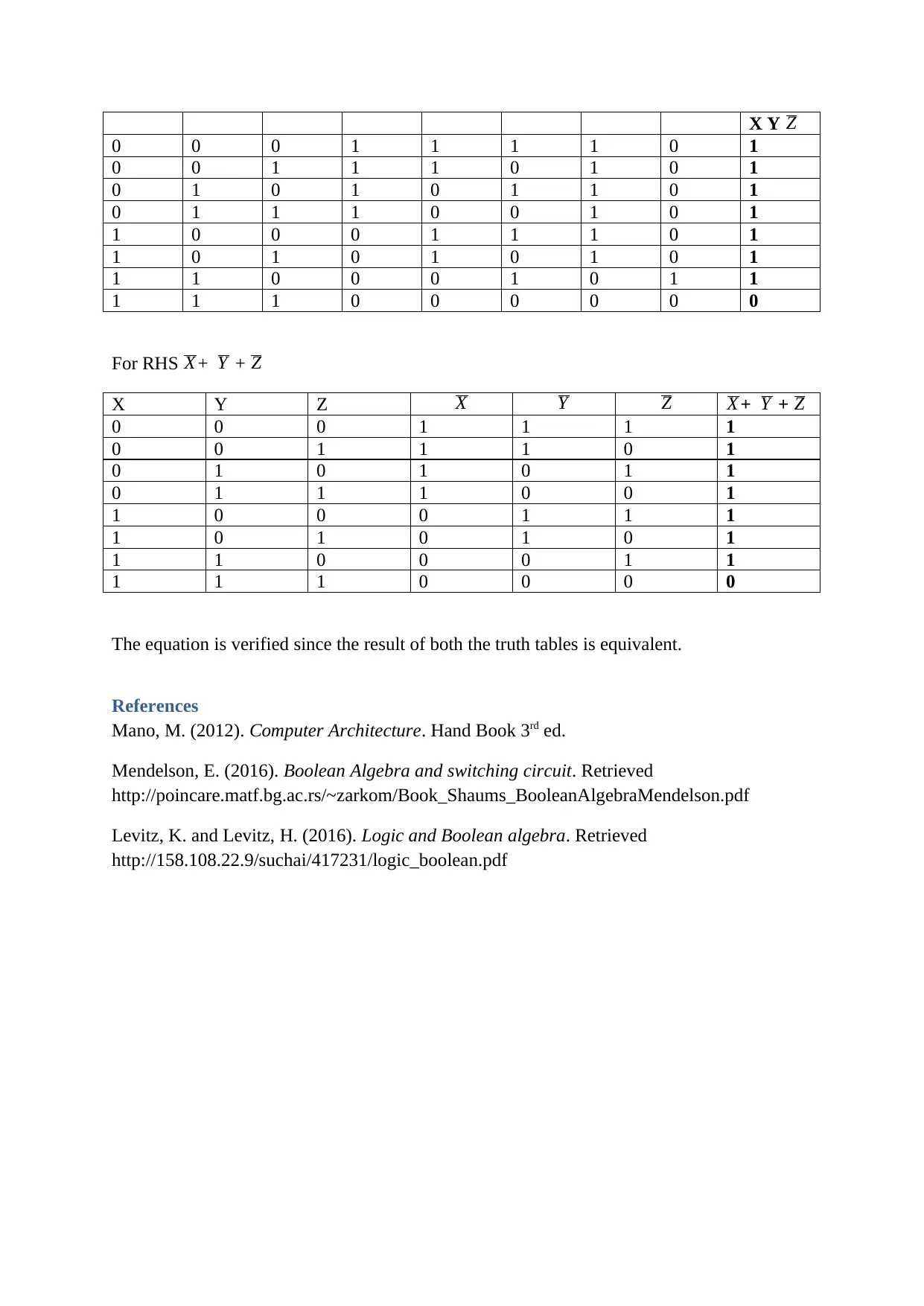
This assignment focuses on computer organization, addressing questions related to number base conversions and logic circuits. It covers converting numbers between different bases such as base 7 to base 2 and base 10 to base 8, including fractional numbers. Additionally, it explores logic circuits, using truth tables to prove the equivalence of two circuits and to simplify a complex circuit into an OR gate. The assignment also verifies a Boolean algebra equation using truth tables, demonstrating the relationship between logical operations. The document concludes with a list of references used in solving the problems. Desklib provides similar solved assignments and resources for students.

Computer Organization

Contents
Question 1:.................................................................................................................................2
Question 2:.................................................................................................................................3
References..................................................................................................................................5

Question 1:
Answer 1:
1) The answer are given below
a) 0*BED is the incorrect notation to convert it into base 3 notation.
b) (321)7 = (10100010)2
Digits 3 2 1
Numbering 2 1 0
First converting base 7 to base 10
3* 72 + 2 * 71 + 1 * 70
147 + 14 + 1
= 162
Now we will convert base 10 to base 2 with the division method
Divisor Dividend Remainder
2 162
2 81 0
2 40 1
2 20 0
2 10 0
2 5 0
2 2 1
2 1 0
(321)7 = (10100010)2
c) (1235)10 = (2323)8
Divisor Dividend Remainder
8 1235
8 154 3
8 19 2
8 2 3
(1235)10 = (2323)8

a) (21.21)8 = (17.265625)10
Place value Tens One Tenth Hundredth
Digit 2 1 2 1
Numbering 81 80 8-1 8-2
= 2 * 81 + 1 * 80 + 2 * 8-1 + 2 * 8-2
= 16 + 1 + 0.125 + 0.03215
=17.265625
(21.21)8 = (17.265625)10
2) One’ complement:
The lowest value is 101
The highest value is 110
Two’s complement
The lowest value is 011
The highest value is 101
Signed magnitude
The lowest value is 001
The highest value is 111
Question 2:
a) The result of the following truth table helps in predicting that the given two circuits
are equivalent or not:
Truth table for circuit one
Operand A Operand B A*B (A AND B) NOT (A AND B)
0 0 0 1
0 1 0 1
1 0 0 1
1 1 1 0
Truth table for circuit two:
Operand A Operand B Operand A NOT Operand B NOT A NOT OR B

NOT
0 0 1 1 1
0 1 1 0 1
1 0 0 1 1
1 1 0 0 0
From the result of both the truth table we are able to measure that both the circuit are
equivalent.
b) The truth table for the given circuit is :
A B NOT A NOT B NOT A
AND NOT
B
A AND B (NOT A
AND NOT
B) OR (A
AND B)
0 0 1 1 1 0 1
0 1 1 0 0 0 0
1 0 1 1 1 0 1
1 1 0 0 0 1 1
The result of the truth table is equivalent to the truth table of the OR gate. Therefore, the
given complete circuit can be replaced with the OR gate.
A B A OR B
0 0 0
0 1 1
1 0 1
1 1 1
The output of table 1 and 2 are equivalent as the signal will off only when both the input are
off otherwise the result is true.
The Logic Diagram of the resultant circuit is:
c) X + Y + X Y Z = X + Y + Z
For LHS X + Y + X Y Z
X Y Z X Y Z X + Y X Y Z X + Y +
Operand A
Operand B
Operand A OR Operand B

X Y Z
0 0 0 1 1 1 1 0 1
0 0 1 1 1 0 1 0 1
0 1 0 1 0 1 1 0 1
0 1 1 1 0 0 1 0 1
1 0 0 0 1 1 1 0 1
1 0 1 0 1 0 1 0 1
1 1 0 0 0 1 0 1 1
1 1 1 0 0 0 0 0 0
For RHS X + Y + Z
X Y Z X Y Z X + Y + Z
0 0 0 1 1 1 1
0 0 1 1 1 0 1
0 1 0 1 0 1 1
0 1 1 1 0 0 1
1 0 0 0 1 1 1
1 0 1 0 1 0 1
1 1 0 0 0 1 1
1 1 1 0 0 0 0
The equation is verified since the result of both the truth tables is equivalent.
References
Mano, M. (2012). Computer Architecture. Hand Book 3rd ed.
Mendelson, E. (2016). Boolean Algebra and switching circuit. Retrieved
http://poincare.matf.bg.ac.rs/~zarkom/Book_Shaums_BooleanAlgebraMendelson.pdf
Levitz, K. and Levitz, H. (2016). Logic and Boolean algebra. Retrieved
http://158.108.22.9/suchai/417231/logic_boolean.pdf