Computer Architecture and Organization Assignment Solution

This document presents a detailed solution to a computer architecture and organization assignment. The solution covers several key topics, including binary, one's complement, two's complement, and signed magnitude representations. It includes conversions between binary, octal, hexadecimal, and base-5 number systems, along with decimal conversions. Furthermore, the assignment addresses Boolean algebra, proving identities and simplifying expressions. The solution also involves constructing a truth table, deriving a minimized Boolean function using a Karnaugh map, and designing a corresponding circuit diagram. Finally, it includes the analysis of assessment criteria for passing a subject with multiple components.

UNIVERSITY AFFILIATION
DEPARTMENT OR FACULTY
COURSE CODE
COMPUTER ARCHITECTURE AND ORGANIZATION
STUDENT NAME
STUDENT REGISTRATION NUMBER
DATE OF SUBMISSION
1

QUESTION 1
(a) Given a tiny computer that has a word size of 8 bits, what are the smallest negative numbers
and the largest positive numbers that this computer can represent in each of the following
representations? (2+2+2+2=8 marks)
i. One's complement
For the one’s complement,
01111111=27 −1=127 … for largest positive number
10000000=−(01111111)=−(27−1)=−127 … for largest negative number
ii. Two's complement
For the two’s complement,
01111111=27 −1=127 … for largest positive number
10000000=−(10000000)=−(27)=−128 … for largest negative number
iii. Signed magnitude
−12710 ¿+12710
The leftmost bit is the sign bit. It represents the sign of the magnitude,
Binary equivalent of 12710=111 11112
Therefore,
−12710=1 111 11112
to
+12710 =0 11111112
iv. Unsigned magnitude
smallest unsigned=010 , largest unsigned=25510
000000002=010 ¿ 111111112=25510
(b) Convert the followings: (7 marks)
i. 0x5AB into Octal
0 x 5 AB∈hexadecimal=5 AB16
Conversion: Hexadecimal to Binary to Octal
2

To binary,
0 x 5=0101 b
0 xA=1010 b
0 xB=1011b
Therefore,
0 x 5 AB=010110101011 b
To octal,
¿ 010 110 101011 b → octal
¿ 26538
ii. 101101.1012 into Decimal
Factor 25 24 23 22 21 20 2-1 2-2 2-3
Binary 1 0 1 1 0 1 . 1 0 1
Decimal 32 0 8 4 0 1 . 0.5 0 0.125
¿ 32+8+ 4+1+0.5+ 0.125
¿ 45.62510
iii. 12348 into Binary
¿ octal ¿ binary
1 2 3 4
001 010 011 100
¿ 001 010 011100 b
¿ 10100111002
iv. 679810 into Base 5 number
¿ 679810
¿ 6798
5 =1359+ 3
5 →3
¿ 1359
5 =271+ 4
5 → 4
¿ 271
5 =54+ 1
5 → 1
¿ 54
5 =10+ 4
5 → 4
¿ 10
5 =2+0
5 → 0
3

¿ 2
5 → 2
¿ 2041435
v. 976.6310 into Binary
Dividing the section into two,
The whole part,
¿ 976
2 =488 R → 0
¿ 488
2 =244 R → 0
¿ 244
2 =122 R → 0
¿ 122
2 =61 R → 0
¿ 61
2 =30 R → 1
¿ 30
2 =15 R → 0
¿ 15
2 =7 R → 1
¿ 7
2 =3 R→ 1
¿ 3
2 =1 R → 1
¿ 1
2 =1 R →1
¿ 11110100002=97610
The fractional part,
¿ .63∗2=1 .26
¿ .26∗2=0 .52
¿ .52∗2=1.04
¿ .04∗2=0.08
4

¿ .08∗2=0 .16
¿ .16∗2=0 .32
¿ .32∗2=0 .64 …. starts recurring
¿ 0.10100002=0.6310
Therefore,
¿ 1111010000.10100002
vi. 1001001011 into Hexadecimal
Dividing into four-bit words,
¿ 0010 0100 1011
¿ 0 x 24 B
vii. 10011110 (8-bit 2’s complement representation) to Decimal
1 0011110=signed value ( negative )
Changing the sign to get the magnitude of the number,
1 0011110→ 011000012 +12=011000102
Converting to decimal,
011000102 →9810
For a negative number,
¿−9810
QUESTION 2
(a) Using basic Boolean algebra identities for Boolean variables X and Y, prove that
X ’ (X +Y )+( XX+Y )(Y ’+ X )=Y +X . Please show all steps and mention the identities
used. (6 marks)
Simplifying the Boolean algebra,
X ’ (X +Y )+( XX+Y )(Y ’+ X )=Y +X
( x' x +x' y ) + ( xx + y ) ( y' + x )
But , x' x → 0
Therefore,
¿ x' y + ( xx + y ) ( y'+ x )
5

¿ x' y + ( xx y'+ xxx + y y' + xy )
But , xxx → x
¿ yy ' →0
while , xx y' → x y'
Hence,
¿ x' y +x y' + x + xy
¿ x' y + x ( y' +1 ) +xy
¿ ( y' +1 ) =1
¿ x' y + x + xy
¿ y ( x'+ x ) + x
¿ ( x'+ 1 )=1
¿ y +x
(b) A subject has 4 assessments, such as Assignment, Blog, Discussion Forum and Quiz. In
order to pass in the subject, a student must get as below:
 Assignment component must pass (50 or above)
 Any 2 more assessments must pass
 Fail otherwise
Construct a truth table and find the minimized Boolean function. Draw a circuit diagram
for the Boolean function. (9 marks)
Let,
A=assignment component
B=Blog
C=discussion Forum
D=Quiz
A B C D Output
0 0 0 0 0
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 0
0 1 0 1 0
0 1 1 0 0
0 1 1 1 0
1 0 0 0 0
1 0 0 1 0
1 0 1 0 0
1 0 1 1 1
1 1 0 0 0
6

1 1 0 1 1
1 1 1 0 1
1 1 1 1 1
¿ ABCD+ ABC D' + ABC' D+ A B' CD
Using the Karnaugh map to simplify the output,
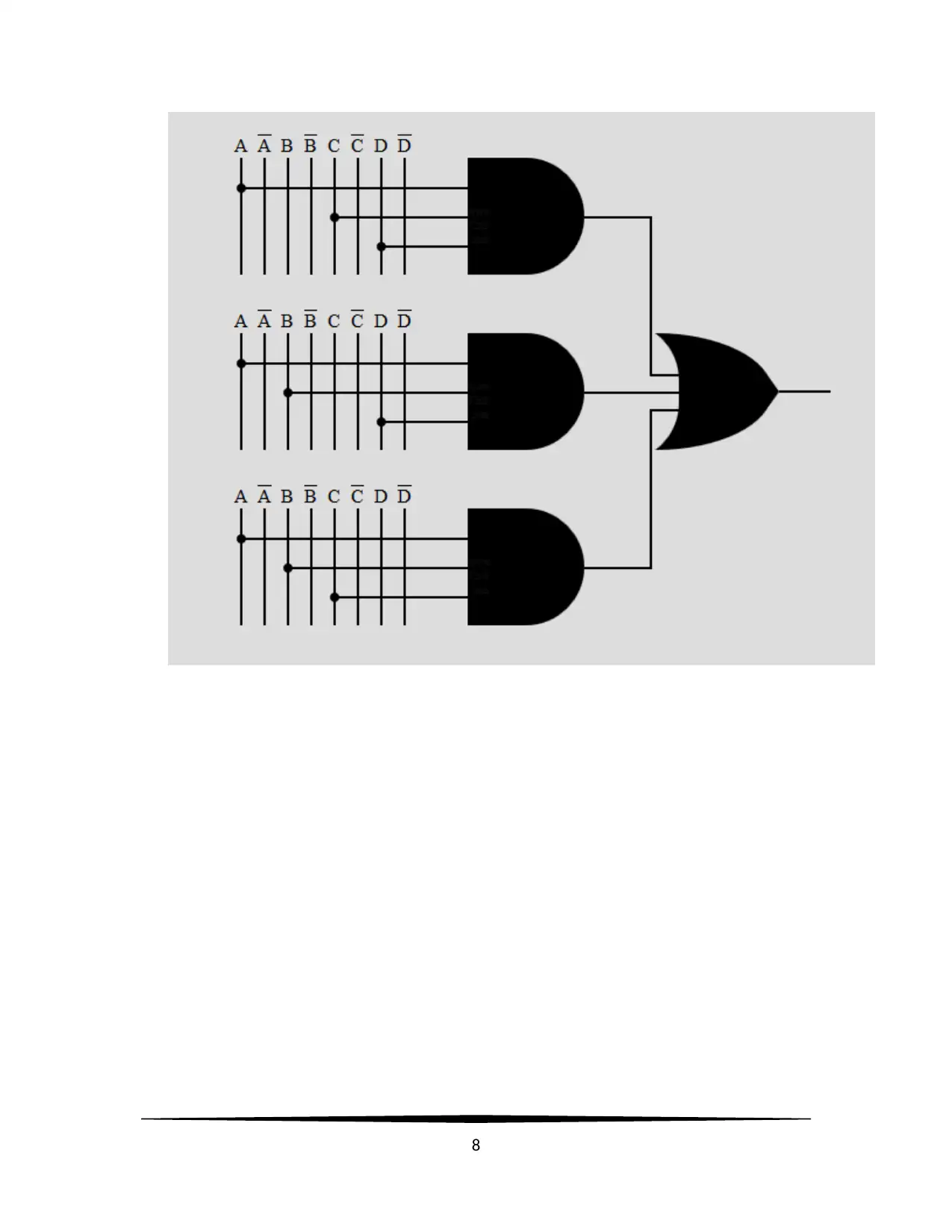
y= ACD+ ABC + ABD
The circuit design,
7

8