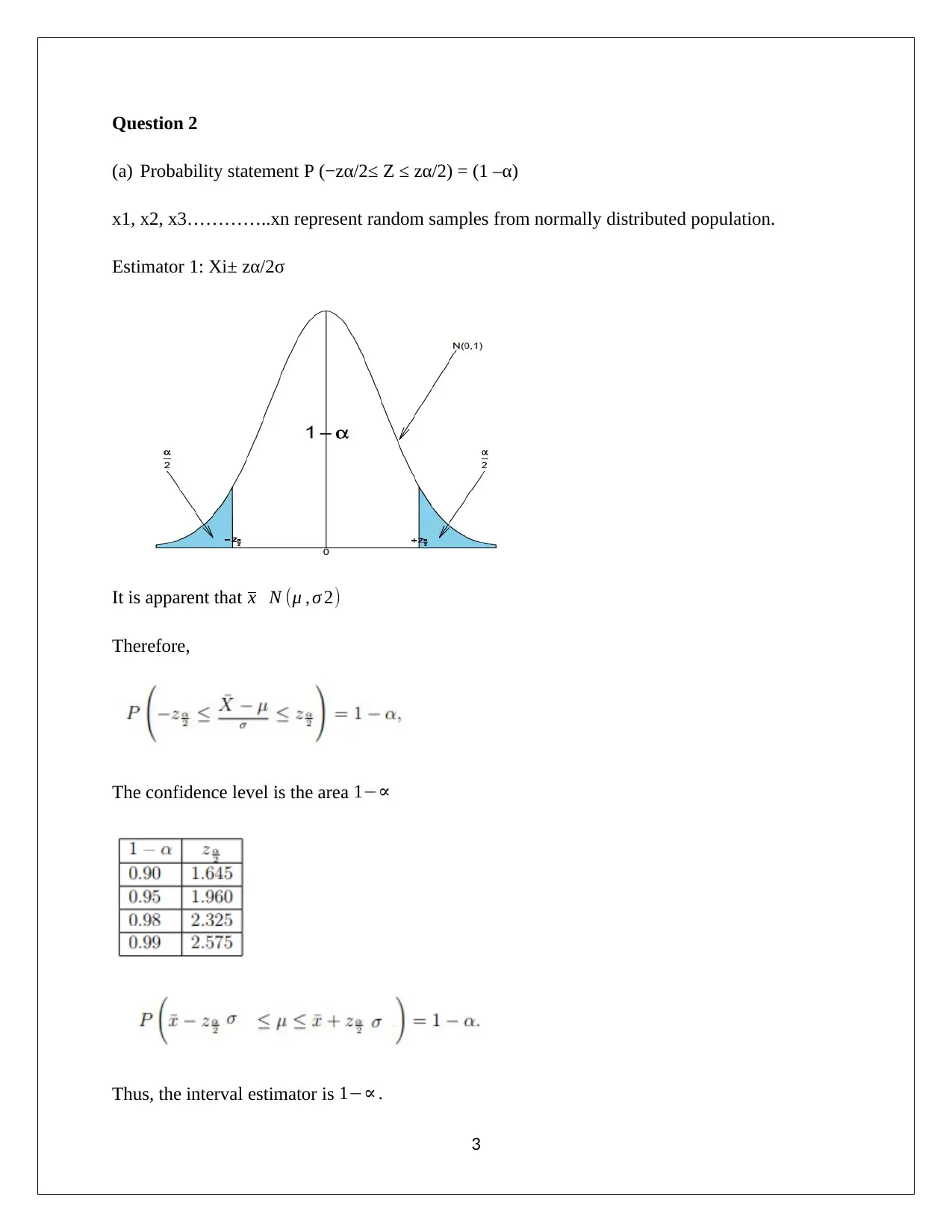
Quantitative Methods: Analyzing Confidence Intervals and Hypothesis

This assignment solution covers key concepts in quantitative methods, including the calculation and interpretation of confidence intervals and hypothesis testing. It begins with calculating a 95% confidence interval for a given dataset and then conducts a hypothesis test to determine if standard wine bottles contain an average of 750 ml. The solution also discusses the selection and appropriate use of different statistical estimators, considering scenarios where data may not be normally distributed. Part B consists of multiple-choice questions on related statistical concepts, providing a comprehensive overview of the topics. Desklib offers this assignment and many more to help students excel.

QUANTITATIVE METHODS
Student Name
[Pick the date]

Part A
Question 1
(a) Calculation of 95% confidence interval
Set of data observation = n= 12
Average of data (x bar) = (745+752+754+745+748+753+746+742+745+748+741+746)/12
=747.083
Standard deviation
For 95% confidence interval, z value = 1.960
1

(b) Null and alternative hypotheses
Dof =12−1=11
Hypothesis testing = Two tailed test
The respective p value (for input, test statistics, dof and two tailed test) = 0.0321
Let the alpha (significance level) = 5%
The p value << alpha
Reject null hypothesis and can be concluded that “standard bottles of wine does not contain an
average of exactly 750 ml.”
(c) A key observation is that the confidence interval computed in part (a) does not contain the
value 750 which implies that it is not a possible value and hence there is significant
difference from 750 ml. This clearly is same as the outcome in part (b).
2

Question 2
(a) Probability statement P (−zα/2≤ Z ≤ zα/2) = (1 –α)
x1, x2, x3…………..xn represent random samples from normally distributed population.
Estimator 1: Xi± zα/2σ
It is apparent that x N (μ , σ 2)
Therefore,
The confidence level is the area 1−∝
Thus, the interval estimator is 1−∝ .
3

(b) Estimator 2 would be commonly used owing to the computation of the interval estimate with
a higher accuracy and would also capture the basic idea of accuracy of population mean estimate
enhancing with the sample size increasing. This is also in line with the Central Limit Theorem
and unlike estimator (1) does not provide a conservative estimate (Newcombe 189).
(c) A key problem with regards to the usage of estimator (2) arises when the underlying variable
X does not exhibit a normal distribution. In such situation, the basic assumption about higher
sample size being more accurate is not necessarily true. As a result, it would make sense to use
estimator (1) which is not linked to the normality assumption and therefore provides a more
conservative interval which is more accurate in this scenario (Harmon 102).
(d) For the appropriate use of estimator (2) when X is not normally distributed, it would be
imperative for the sample size to be large so that in accordance with Central Limit Theorem, the
deviations from the mean can reduce at higher sample sizes.
Part B
1. D
2. E
3. D
4. A
5. C
6. B
4

References
Harmon, Mark. Hypothesis Testing in Excel - The Excel Statistical Master .Florida: Mark
Harmon, 2015.
Newcombe, Robert. Confidence intervals for Proportions and Related Measures of Effect Size.
Sydney: CRC Press 2016.
5