University Calculus Assignment on Conic Sections and Polar Equations

This assignment solution covers various aspects of conic sections, including hyperbolas, parabolas, and ellipses. It begins with finding the standard form of a hyperbola given its foci and vertices, followed by determining the focus and directrix of parabolas. The solution then identifies conic sections represented by polar equations and addresses the transformation of equations in rotated systems. Further questions involve identifying conic sections without completing the square, finding vertices and foci of hyperbolas, eliminating parameters from parametric equations, and solving problems related to elliptical orbits and the distance of Halley's Comet. The assignment also includes problems on finding the standard form of an ellipse, identifying hyperbolas from graphs, parameterizing curves, and applying conic section concepts to real-world scenarios like suspension bridges and baseball trajectories. Finally, it includes questions on finding the directrix, focus, and symmetry of various conic sections.

1. Find the standard form of the equation of the hyperbola satisfying the following conditions.
Foci: (–10, 0), (10, 0); vertices: (–4, 0), (4,0)
A.
B.
C.
D.
Solution: Given that the foci and vertices of the hyperbola are respectively.
That is this gives and vertices this gives . We
know that . Substitute the values of a and c we get
Since, the standard form of hyperbola is . Substitute the values of a and b we get,
Hence, option D is correct.
2. Find the focus and directrix of the parabola with the following equation:
x2 = 36y

A. focus: (0, 9); directrix: y = –9
B. focus: (9, 0); directrix: y = 9
C. focus: (0, -9); directrix: y = 9
D. focus: (9, 0); directrix: x = –9
Solution: We know that if the general form of parabola is , then its focus and directrix
are and respectively. Now compare with we get
So, focus: and directrix:
Hence, option A is correct.
3. Find the focus and directrix of the parabola with the following equation:
y2 = 12x
A. focus: (3, 0); directrix: x = –3
B. focus: (0, -3); directrix: y = –3
C. focus: (3, 0); directrix: x = 3
D. focus: (0, 3); directrix: y = –3

Solution: We know that if the general form of parabola is , then its focus and directrix
are and respectively. Now compare with we get
So, focus: and directrix:
Hence, option A is correct.
4. Identify the conic section that the following polar equations represents:
A. ellipse
B. hyperbola
C. circle
D. parabola
Solution: Compare the conic section with we get
. Since, so the given conic is in ellipse. Hence option A is correct.
5. Write the following equation in terms of a rotated x′y′-system using θ, the angle of rotation.
Write the equation involving x′ and y′ in standard form.
xy + 16 = 0; θ = 45°

A.
B.
C.
D.
Solution: .
Given that so,
Since, . Substitute the values of x and y we get
Hence, option A is correct.
6. Identify the following equation without completing the square:

5x2 – 6y2 + 2x – 3y – 5 = 0
A. hyperbola
B. circle
C. ellipse
D. parabola
Solution: Note that a non- degenerate conic section of the form
where A and C are non zero, is
A circle if
A parabola if
An ellipse if and
A hyperbola if
Here and
Therefore, given conic is a hyperbola. Hence, option A is correct.
7. Find the vertices and locate the foci for the following hyperbola equation:
A. vertices: (–12, 0), (12, 0)

foci: (–5, 0), (5, 0)
B. vertices: (–5, 0), (5, 0)
foci: (–13, 0), (13, 0)
C. vertices: (0, –12), (0, 12)
foci: (–13, 0), (13, 0)
D. vertices: (–12, 0), (12, 0)
foci: (–13, 0), (13, 0)
Solution: Compare the hyperbola with we get
And
We know that
So, the vertices are and foci are . Hence, option D is correct.
8. Eliminate the parameter from the parametric form of the following equation:
x = a + bt; y = c + dt
A.
B.
C.
D.

Solution: Given that . Simplify we get
Equating the both values of t we get,
Hence, option B is correct.
9. Halley's Comet has an elliptical orbit with the sun at one focus. Its orbit shown below is given
approximately by . In the formula, r is measured in astronomical units. (One
astronomical unit is the average distance from Earth to the sun, approximately 93 million miles.)
Find the distance from Halley's Comet to the sun at its greatest distance from the sun. Round to
the nearest hundredth of an astronomical unit and the nearest million miles.
A. 11.36 astronomical units; 1057 million miles

B. 5.57 astronomical units; 518 million miles
C. 5.68 astronomical units; 528 million miles
D. 295.68 astronomical units; 27,498 million miles
Solution: Given . Differentiate with respect to we get
Form maximum, we get
.
So maximum value at is
Since, One astronomical unit = 93 million miles
So, 295.68 astronomical units = 27,498 million miles million miles
Hence, option D is correct.
10. Find the standard form of the equation of the ellipse satisfying the following conditions.
Endpoints of major axis: (–4, –8) and (–4, 4); endpoints of minor axis: (–9, –2) and (1, - 2);

A.
B.
C.
D.
Solution: Given that endpoints of major axis: (–4, –8) and (–4, 4); endpoints of minor axis: (–9,
–2) and (1, -2).
We know that length of major axis is and length of minor axis is
and center of the ellipse is
So, the equation of ellipse is
Substitute the values of a, b and center we get
Hence, option B is correct.
11. What's the standard form of the equation of the following hyperbola?

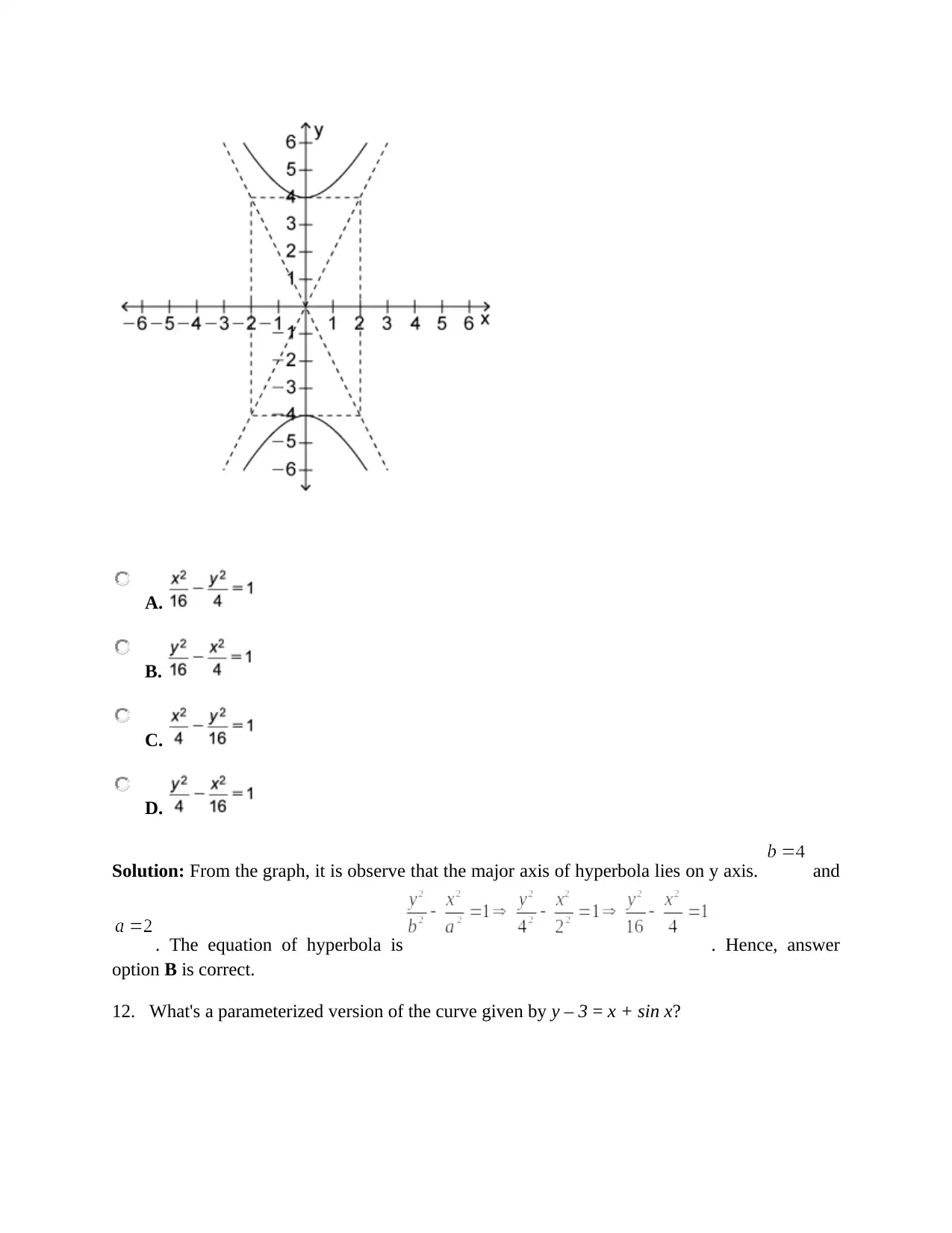
A.
B.
C.
D.
Solution: From the graph, it is observe that the major axis of hyperbola lies on y axis. and
. The equation of hyperbola is . Hence, answer
option B is correct.
12. What's a parameterized version of the curve given by y – 3 = x + sin x?

A. t = x, sin x – y + 3
B. t = –3 = y, t + sin t = x
C. y = –3t, x = y + sin t
D. x = t, y = t + sin t + 3
Solution: Given . Let this implies that
Hence, answer option D is correct.
13. An experimental model for a suspension bridge is built. In one section, cable runs from the
top of one tower down to the roadway, just touching it there, and up again to the top of a second
tower. The towers stand 60 inches apart. At a point between the towers and 18 inches along the
road from the base of one tower, the cable is 1.44 inches above the roadway. Find the height of
the towers.
A. 9.5 in
B. 11 in
C. 8.5 in
D. 9 in
Solution:

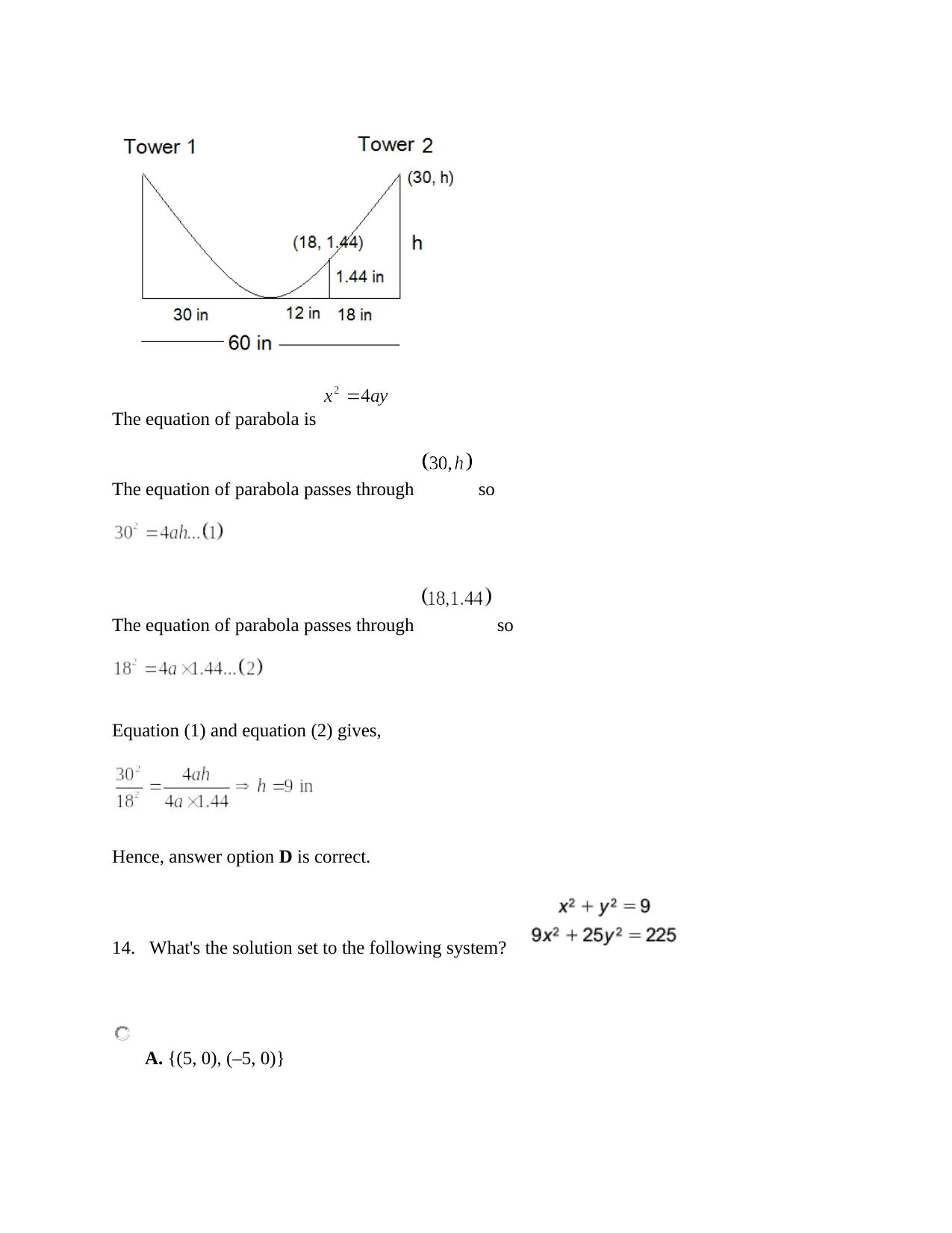
The equation of parabola is
The equation of parabola passes through so
The equation of parabola passes through so
Equation (1) and equation (2) gives,
Hence, answer option D is correct.
14. What's the solution set to the following system?
A. {(5, 0), (–5, 0)}

B. {(3, 0), (–3, 0)}
C. {(0, 5), (0, –5)}
D. {(0, 3), (0, –3)}
Solution: Given that
From equation (1)
From equation (2)
For , the value of x is 0.
Hence, the solutions of the given system are . Therefore answer option D is
correct.
15. A batter hits a baseball from 3 feet above home plate along the path x = 69t, y = 3 + 40t –
16t2. How long is the ball in flight, and how far does it travel?

A. 0.389s, 26.8'
B. 2.573s, 177.5'
C. 0.073s, 5.04'
D. 13.723s, 946.9'
Solution: Given that the vertical and horizontal paths are x = 69t, y = 3 + 40t – 16t2 respectively.
Solve for
Use general quadratic formula
At
Hence, answer option B is correct.
16. What's the equation of the directrix for the conic section
A. y = –6

B. x = 2
C. y = 6
D. x = –3
Solution: Given that equation of conic section is . We know that the directrix of
polar equation is . Here so the equation of directrix is .
17. Which graph matches the polar equation below?
A.

B.
C.

D.
Solution: The graph of the polar curve is
Hence, answer option D is correct.
18. What's the focus of the parabola x2 = –4y

A. (0, 1)
B. (0, –1)
C. (–1, 0)
D. (1, 0)
Solution: Given parabola is . Note that the focus of standard form of parabola
is . Here . So, focus is . Hence, answer option B is
correct.
19. Which of the following is symmetrical about the polar (or x) axis?
A.
B.
C.
D.
Solution: A polar equation is symmetrical about x –axis if and this condition is
satisfied by option C. Hence, answer option C is correct.
20. Which of these is a valid geometric definition of a parabola?

A. The graph of y = x2
B. The set of points equidistant from a directrix and a focus not on the directrix
C. The set of points equidistant from two asymptotes that cross at the origin.
D. The set of points equidistant from two foci
Solution: A parabola is defined as follows: For a given point, called the focus, and a given line
not through the focus, called the directrix, a parabola is the locus of points such that the distance
to the focus equals the distance to the directrix.
Hence, answer option B is correct.