Control Systems Homework Assignment Solution and Response Analysis
VerifiedAdded on 2022/08/22
|13
|791
|25
Homework Assignment
AI Summary
This document presents a complete solution to a control systems homework assignment, analyzing two different problems. The first problem focuses on determining the transfer function of an open-loop system and then analyzing the response of both unity and non-unity feedback systems. The solution involves deriving the transfer functions, calculating time constants, and comparing the transient responses of each system, including rise time and settling time. The second problem delves into a second-order system, deriving the transfer function from a given response graph. It calculates key parameters such as natural frequency and damping ratio. Furthermore, the solution compares the performance of open-loop, unity feedback, and non-unity feedback systems, including their stability and transient response characteristics. The document includes relevant graphs illustrating system responses and concludes with a bibliography of cited sources.

1
Control systems
Student’s Name
Institutional Affiliation
Date
Control systems
Student’s Name
Institutional Affiliation
Date
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
2
Q1
a)
The general transfer function is given as,
G ( s )= k
(1+ τs)
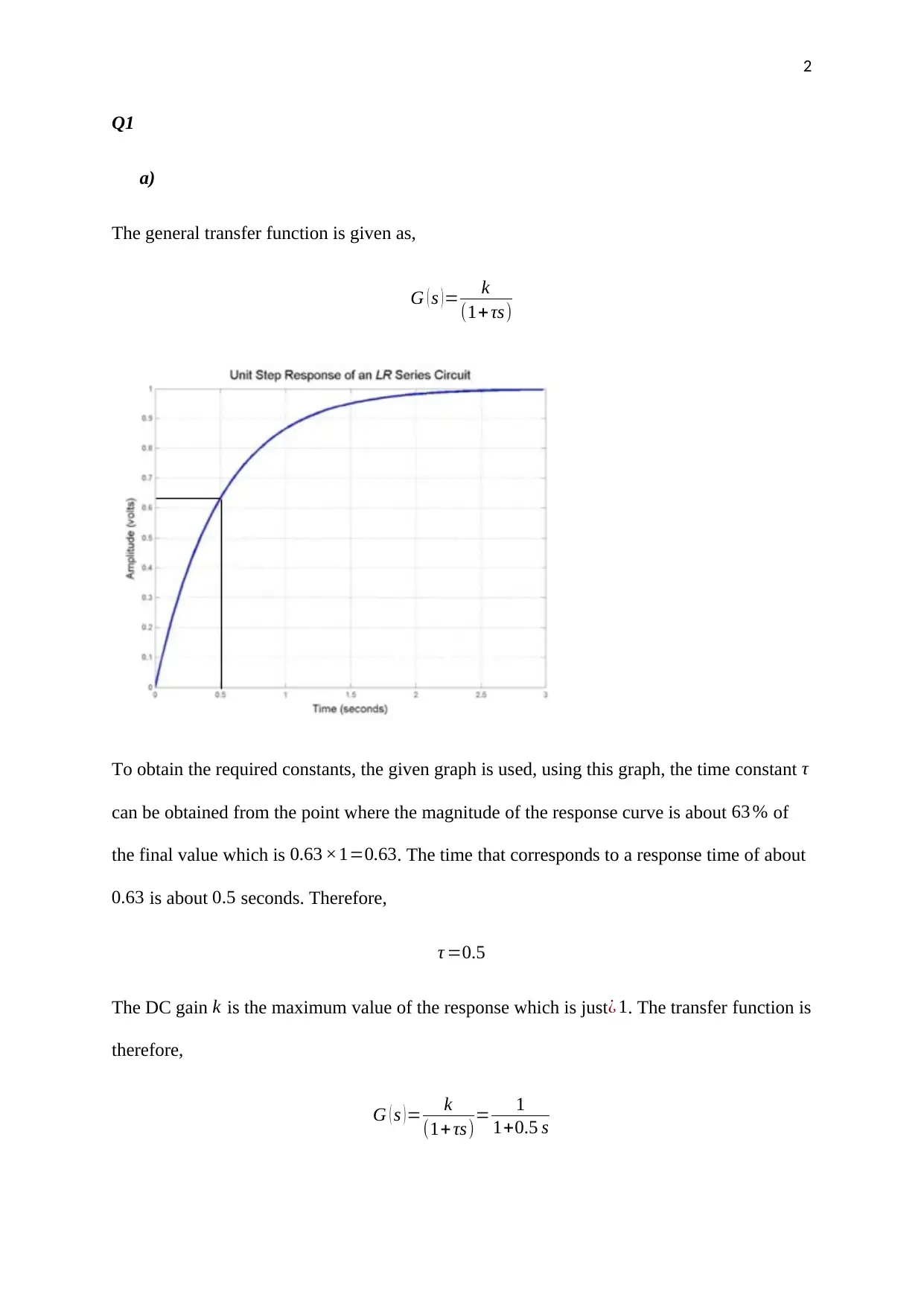
To obtain the required constants, the given graph is used, using this graph, the time constant τ
can be obtained from the point where the magnitude of the response curve is about 63 % of
the final value which is 0.63 ×1=0.63. The time that corresponds to a response time of about
0.63 is about 0.5 seconds. Therefore,
τ =0.5
The DC gain k is the maximum value of the response which is just¿ 1. The transfer function is
therefore,
G ( s )= k
(1+ τs)= 1
1+0.5 s
Q1
a)
The general transfer function is given as,
G ( s )= k
(1+ τs)
To obtain the required constants, the given graph is used, using this graph, the time constant τ
can be obtained from the point where the magnitude of the response curve is about 63 % of
the final value which is 0.63 ×1=0.63. The time that corresponds to a response time of about
0.63 is about 0.5 seconds. Therefore,
τ =0.5
The DC gain k is the maximum value of the response which is just¿ 1. The transfer function is
therefore,
G ( s )= k
(1+ τs)= 1
1+0.5 s
3
G ( s )= 2
s +2
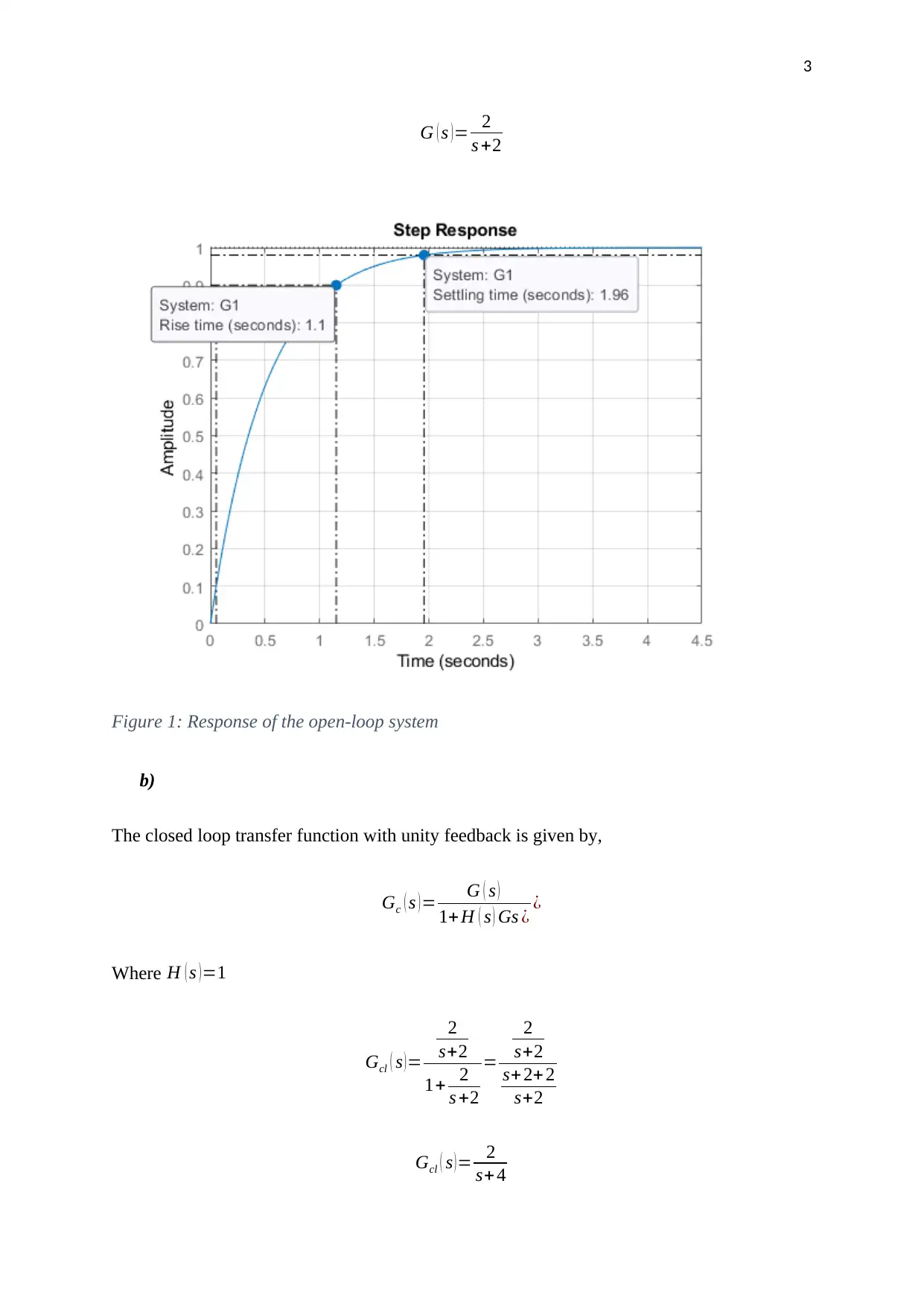
Figure 1: Response of the open-loop system
b)
The closed loop transfer function with unity feedback is given by,
Gc ( s ) = G ( s )
1+ H ( s ) Gs ¿ ¿
Where H ( s )=1
Gcl ( s )=
2
s+2
1+ 2
s +2
=
2
s+2
s+ 2+ 2
s+2
Gcl ( s ) = 2
s+ 4
G ( s )= 2
s +2
Figure 1: Response of the open-loop system
b)
The closed loop transfer function with unity feedback is given by,
Gc ( s ) = G ( s )
1+ H ( s ) Gs ¿ ¿
Where H ( s )=1
Gcl ( s )=
2
s+2
1+ 2
s +2
=
2
s+2
s+ 2+ 2
s+2
Gcl ( s ) = 2
s+ 4
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
4
Gcl ( s ) = 0.5
1+0.25 s
From which,
τ =0.25
k =0.5
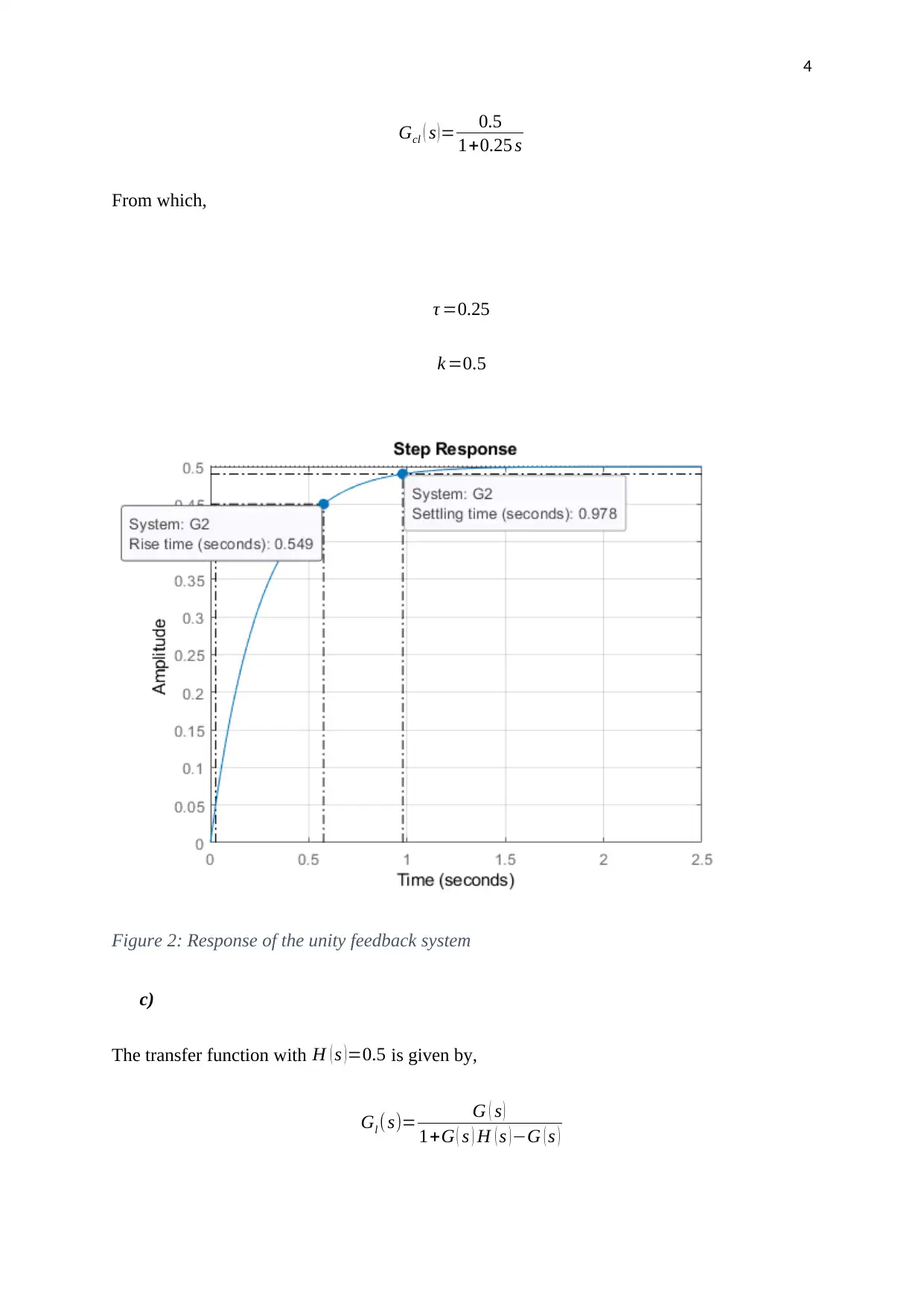
Figure 2: Response of the unity feedback system
c)
The transfer function with H ( s )=0.5 is given by,
Gl ( s)= G ( s )
1+G ( s ) H ( s )−G ( s )
Gcl ( s ) = 0.5
1+0.25 s
From which,
τ =0.25
k =0.5
Figure 2: Response of the unity feedback system
c)
The transfer function with H ( s )=0.5 is given by,
Gl ( s)= G ( s )
1+G ( s ) H ( s )−G ( s )
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
5
Gl ( s)=
2
s+ 2
1+ 2
s+2 H ( s ) − 2
s+ 2
Gl (s)=
2
s +2
1+ 2( 0.5)
s +2 − 2
s+2
Gl ( s )= 2
s +1
This gives,
τ =1
k =2
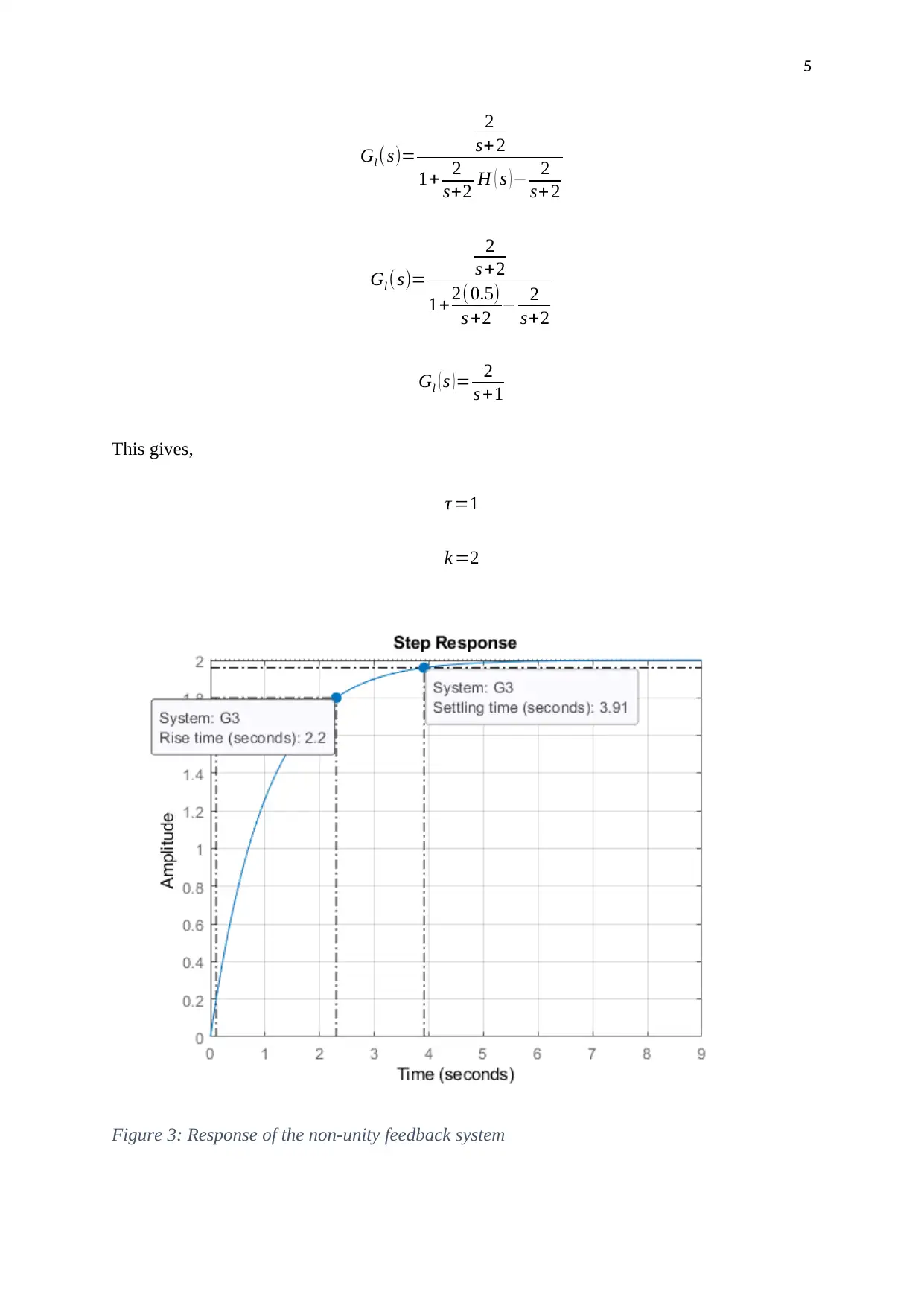
Figure 3: Response of the non-unity feedback system
Gl ( s)=
2
s+ 2
1+ 2
s+2 H ( s ) − 2
s+ 2
Gl (s)=
2
s +2
1+ 2( 0.5)
s +2 − 2
s+2
Gl ( s )= 2
s +1
This gives,
τ =1
k =2
Figure 3: Response of the non-unity feedback system
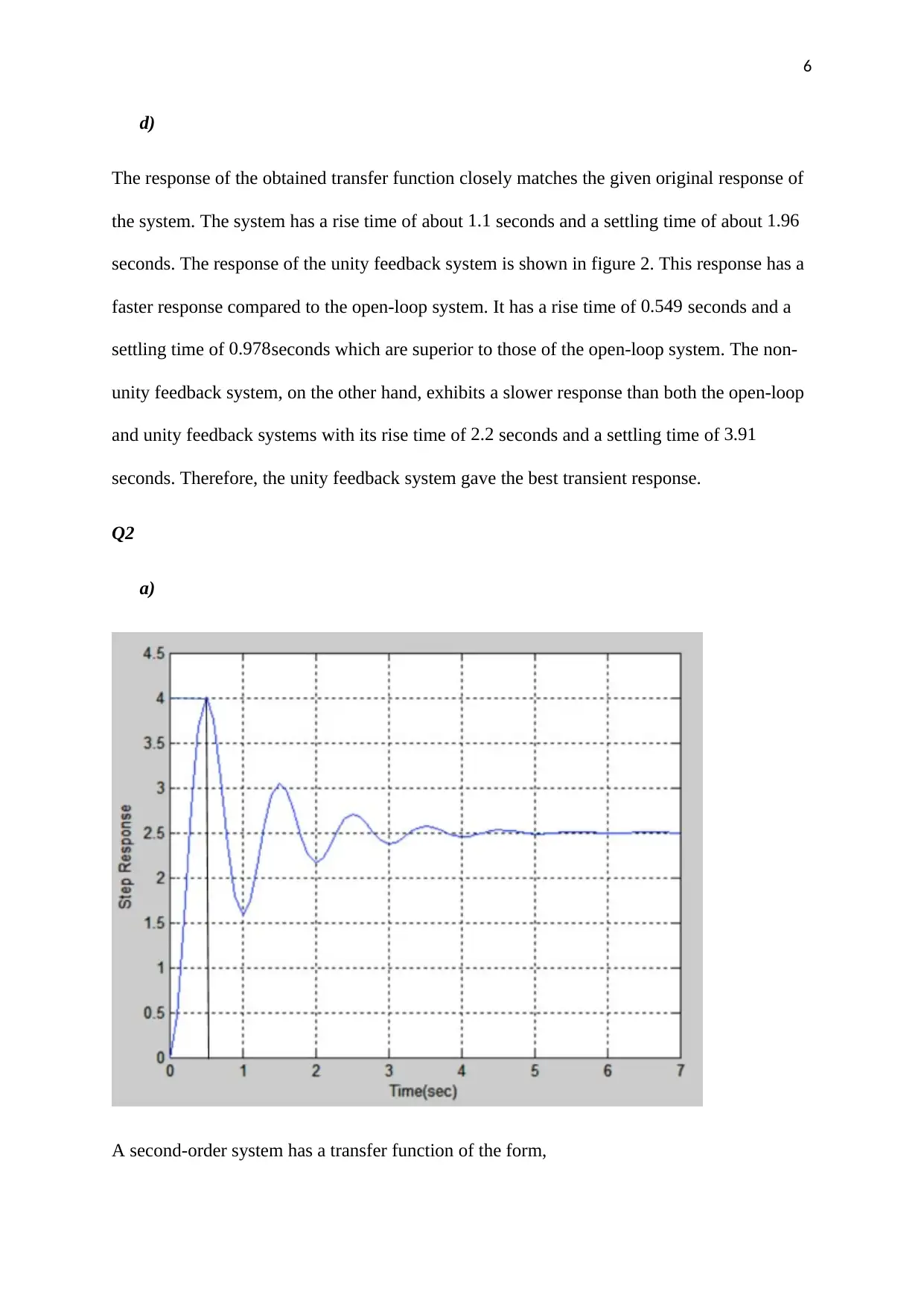
6
d)
The response of the obtained transfer function closely matches the given original response of
the system. The system has a rise time of about 1.1 seconds and a settling time of about 1.96
seconds. The response of the unity feedback system is shown in figure 2. This response has a
faster response compared to the open-loop system. It has a rise time of 0.549 seconds and a
settling time of 0.978seconds which are superior to those of the open-loop system. The non-
unity feedback system, on the other hand, exhibits a slower response than both the open-loop
and unity feedback systems with its rise time of 2.2 seconds and a settling time of 3.91
seconds. Therefore, the unity feedback system gave the best transient response.
Q2
a)
A second-order system has a transfer function of the form,
d)
The response of the obtained transfer function closely matches the given original response of
the system. The system has a rise time of about 1.1 seconds and a settling time of about 1.96
seconds. The response of the unity feedback system is shown in figure 2. This response has a
faster response compared to the open-loop system. It has a rise time of 0.549 seconds and a
settling time of 0.978seconds which are superior to those of the open-loop system. The non-
unity feedback system, on the other hand, exhibits a slower response than both the open-loop
and unity feedback systems with its rise time of 2.2 seconds and a settling time of 3.91
seconds. Therefore, the unity feedback system gave the best transient response.
Q2
a)
A second-order system has a transfer function of the form,
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

7
G ( s ) = k ss ωn
2
s2 +2 ξ ωn s+ωn
2
The natural frequency and damping ratio can be obtained from the parameters for a second
system. The peak time is about 0.5 seconds from the given graph and its formula is,
t p= π
ωd
=0.5 , ωd = π
0.5 =2 π
Analytically, the damped natural frequency is obtained from the formula,
ωd=ωn √ 1−ξ2=2 π
The settling time is given as 4 seconds according to the 2 % criterion. It is obtained from the
formula,’
ts= 4
ξωn
=4 , ξωn = 4
4 =1
ωn= 1
ξ
Substituting in the equation for damped natural frequency we have,
ωn √1−ξ2=2 π
1
ξ √1−ξ2=2 π = √ 1
ξ2 ( 1−ξ2 )
√ ( 1
ξ2 − ξ2
ξ2 )=2 π = √ ( 1
ξ2 −1 )
( 2 π )2= 1
ξ2 −1
1
ξ2 =1+ 4 π2
G ( s ) = k ss ωn
2
s2 +2 ξ ωn s+ωn
2
The natural frequency and damping ratio can be obtained from the parameters for a second
system. The peak time is about 0.5 seconds from the given graph and its formula is,
t p= π
ωd
=0.5 , ωd = π
0.5 =2 π
Analytically, the damped natural frequency is obtained from the formula,
ωd=ωn √ 1−ξ2=2 π
The settling time is given as 4 seconds according to the 2 % criterion. It is obtained from the
formula,’
ts= 4
ξωn
=4 , ξωn = 4
4 =1
ωn= 1
ξ
Substituting in the equation for damped natural frequency we have,
ωn √1−ξ2=2 π
1
ξ √1−ξ2=2 π = √ 1
ξ2 ( 1−ξ2 )
√ ( 1
ξ2 − ξ2
ξ2 )=2 π = √ ( 1
ξ2 −1 )
( 2 π )2= 1
ξ2 −1
1
ξ2 =1+ 4 π2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

8
ξ2= 1
( 1+4 π2 )
ξ=
√ 1
( 1+4 π2 )
ξ=0.157
The undamped natural frequency is thus,
ωn= 1
ξ = 1
0.157 =6.369 rad /s
The transfer function is thus,
G ( s )= k ss ωn
2
s2 +2 ξ ωn s+ωn
2 = 40.56 k ss
s2+2 s+40.56
From the graph, the DC gain is2.5, therefore,
G ( s )= 101.4
s2 +2 s+ 40.56
ξ2= 1
( 1+4 π2 )
ξ=
√ 1
( 1+4 π2 )
ξ=0.157
The undamped natural frequency is thus,
ωn= 1
ξ = 1
0.157 =6.369 rad /s
The transfer function is thus,
G ( s )= k ss ωn
2
s2 +2 ξ ωn s+ωn
2 = 40.56 k ss
s2+2 s+40.56
From the graph, the DC gain is2.5, therefore,
G ( s )= 101.4
s2 +2 s+ 40.56
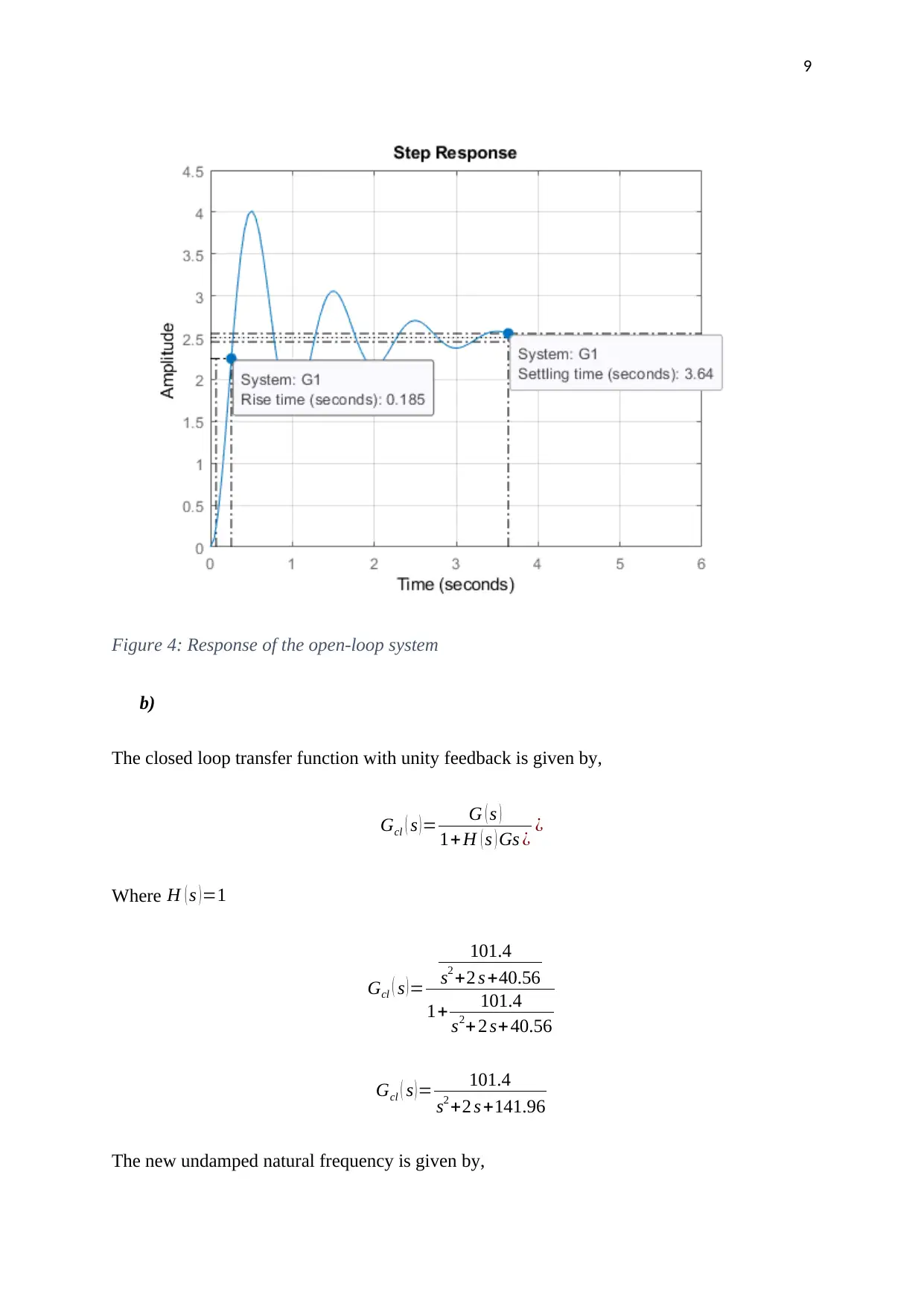
9
Figure 4: Response of the open-loop system
b)
The closed loop transfer function with unity feedback is given by,
Gcl ( s )= G ( s )
1+ H ( s ) Gs ¿ ¿
Where H ( s )=1
Gcl ( s ) =
101.4
s2 +2 s +40.56
1+ 101.4
s2+ 2 s+40.56
Gcl ( s ) = 101.4
s2 +2 s +141.96
The new undamped natural frequency is given by,
Figure 4: Response of the open-loop system
b)
The closed loop transfer function with unity feedback is given by,
Gcl ( s )= G ( s )
1+ H ( s ) Gs ¿ ¿
Where H ( s )=1
Gcl ( s ) =
101.4
s2 +2 s +40.56
1+ 101.4
s2+ 2 s+40.56
Gcl ( s ) = 101.4
s2 +2 s +141.96
The new undamped natural frequency is given by,
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
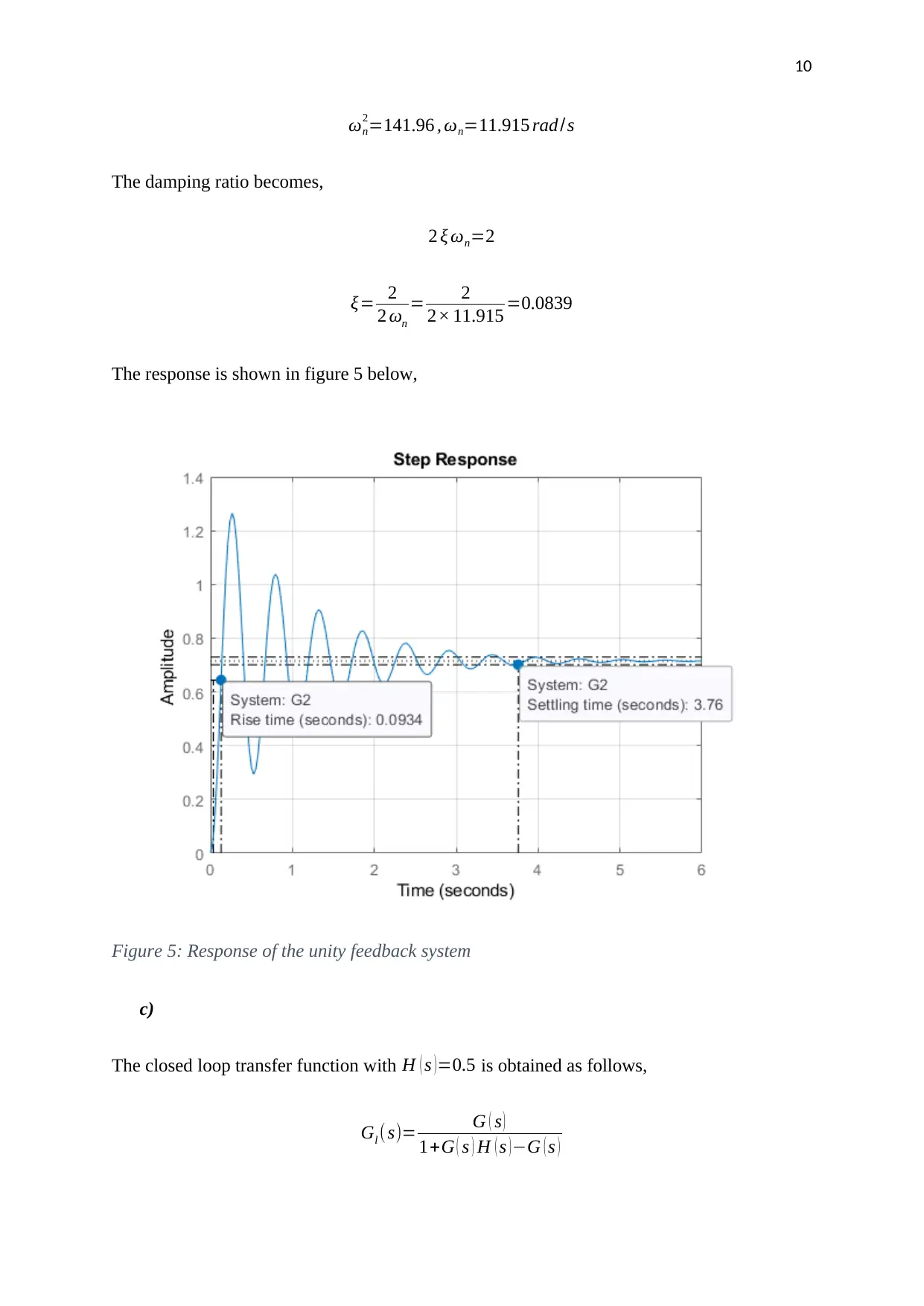
10
ωn
2=141.96 , ωn=11.915 rad /s
The damping ratio becomes,
2 ξ ωn=2
ξ= 2
2 ωn
= 2
2× 11.915 =0.0839
The response is shown in figure 5 below,
Figure 5: Response of the unity feedback system
c)
The closed loop transfer function with H ( s )=0.5 is obtained as follows,
Gl ( s)= G ( s )
1+G ( s ) H ( s )−G ( s )
ωn
2=141.96 , ωn=11.915 rad /s
The damping ratio becomes,
2 ξ ωn=2
ξ= 2
2 ωn
= 2
2× 11.915 =0.0839
The response is shown in figure 5 below,
Figure 5: Response of the unity feedback system
c)
The closed loop transfer function with H ( s )=0.5 is obtained as follows,
Gl ( s)= G ( s )
1+G ( s ) H ( s )−G ( s )
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
11
Gl ( s)=
101.4
s2 +2 s+ 40.56
1+ 101.4
s2 +2 s +40.56 ×0.5− 101.4
s2+ 2 s+ 40.56
Gl ( s)=
101.4
s2 +2 s+ 40.56
1+ 101.4
s2 +2 s +40.56 ×0.5− 101.4
s2+ 2 s+ 40.56
Gl ( s)=
101.4
s2 +2 s+40.56
1+ 50.7
s2 +2 s +40.56 − 101.4
s2 +2 s +40.56
Gl ( s ) =
101.4
s2+ 2 s+ 40.56
1+ 50.7−101.4
s2 +2 s +40.56
=
101.4
s2 +2 s+ 40.56
s2+2 s+ 40.56+50.7−101.4
s2 +2 s+ 40.56
Gl ( s ) =
101.4
s2 +2 s +40.56
s2 +2 s +40.56−50.7
s2 +2 s +40.56
Gl ( s )= 101.4
s2+ 2 s+ 40.56 × s2 +2 s +40.56
s2 +2 s +40.56−50.7 = 101.4
s2 +2 s−10.14
The undamped natural frequency is thus,
ωn
2=−10.14
ωn= √ −10.14
ωn= j √ 10.14= j 3.184 rad /s
The damping ratio becomes,
2 ξ ωn=2
Gl ( s)=
101.4
s2 +2 s+ 40.56
1+ 101.4
s2 +2 s +40.56 ×0.5− 101.4
s2+ 2 s+ 40.56
Gl ( s)=
101.4
s2 +2 s+ 40.56
1+ 101.4
s2 +2 s +40.56 ×0.5− 101.4
s2+ 2 s+ 40.56
Gl ( s)=
101.4
s2 +2 s+40.56
1+ 50.7
s2 +2 s +40.56 − 101.4
s2 +2 s +40.56
Gl ( s ) =
101.4
s2+ 2 s+ 40.56
1+ 50.7−101.4
s2 +2 s +40.56
=
101.4
s2 +2 s+ 40.56
s2+2 s+ 40.56+50.7−101.4
s2 +2 s+ 40.56
Gl ( s ) =
101.4
s2 +2 s +40.56
s2 +2 s +40.56−50.7
s2 +2 s +40.56
Gl ( s )= 101.4
s2+ 2 s+ 40.56 × s2 +2 s +40.56
s2 +2 s +40.56−50.7 = 101.4
s2 +2 s−10.14
The undamped natural frequency is thus,
ωn
2=−10.14
ωn= √ −10.14
ωn= j √ 10.14= j 3.184 rad /s
The damping ratio becomes,
2 ξ ωn=2
12
ξ ωn =1
ξ= 1
ωn
= 1
j3.184
ξ=− j 0.314
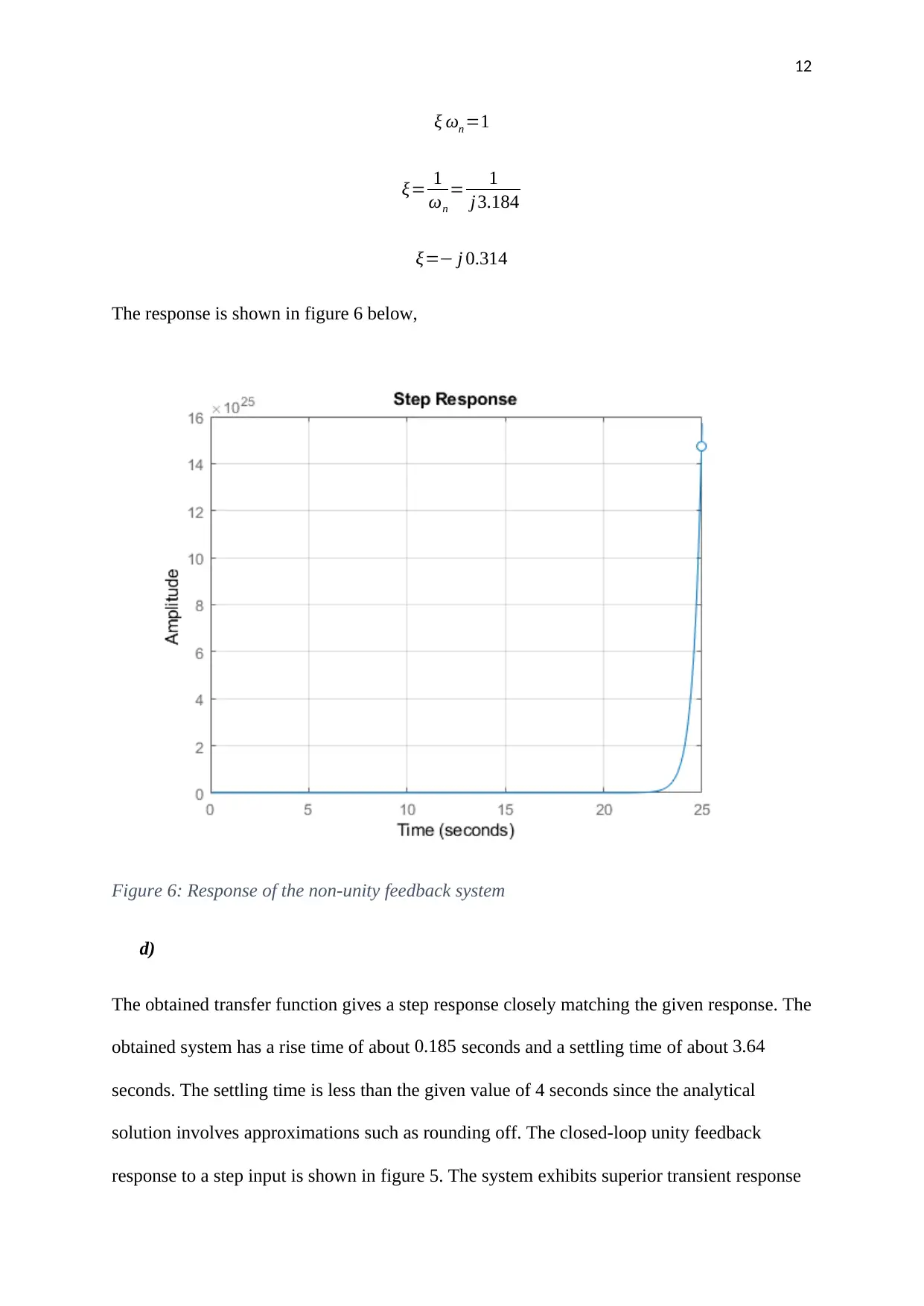
The response is shown in figure 6 below,
Figure 6: Response of the non-unity feedback system
d)
The obtained transfer function gives a step response closely matching the given response. The
obtained system has a rise time of about 0.185 seconds and a settling time of about 3.64
seconds. The settling time is less than the given value of 4 seconds since the analytical
solution involves approximations such as rounding off. The closed-loop unity feedback
response to a step input is shown in figure 5. The system exhibits superior transient response
ξ ωn =1
ξ= 1
ωn
= 1
j3.184
ξ=− j 0.314
The response is shown in figure 6 below,
Figure 6: Response of the non-unity feedback system
d)
The obtained transfer function gives a step response closely matching the given response. The
obtained system has a rise time of about 0.185 seconds and a settling time of about 3.64
seconds. The settling time is less than the given value of 4 seconds since the analytical
solution involves approximations such as rounding off. The closed-loop unity feedback
response to a step input is shown in figure 5. The system exhibits superior transient response
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 13
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





