Control Systems Analysis Coursework: First and Second Order Systems

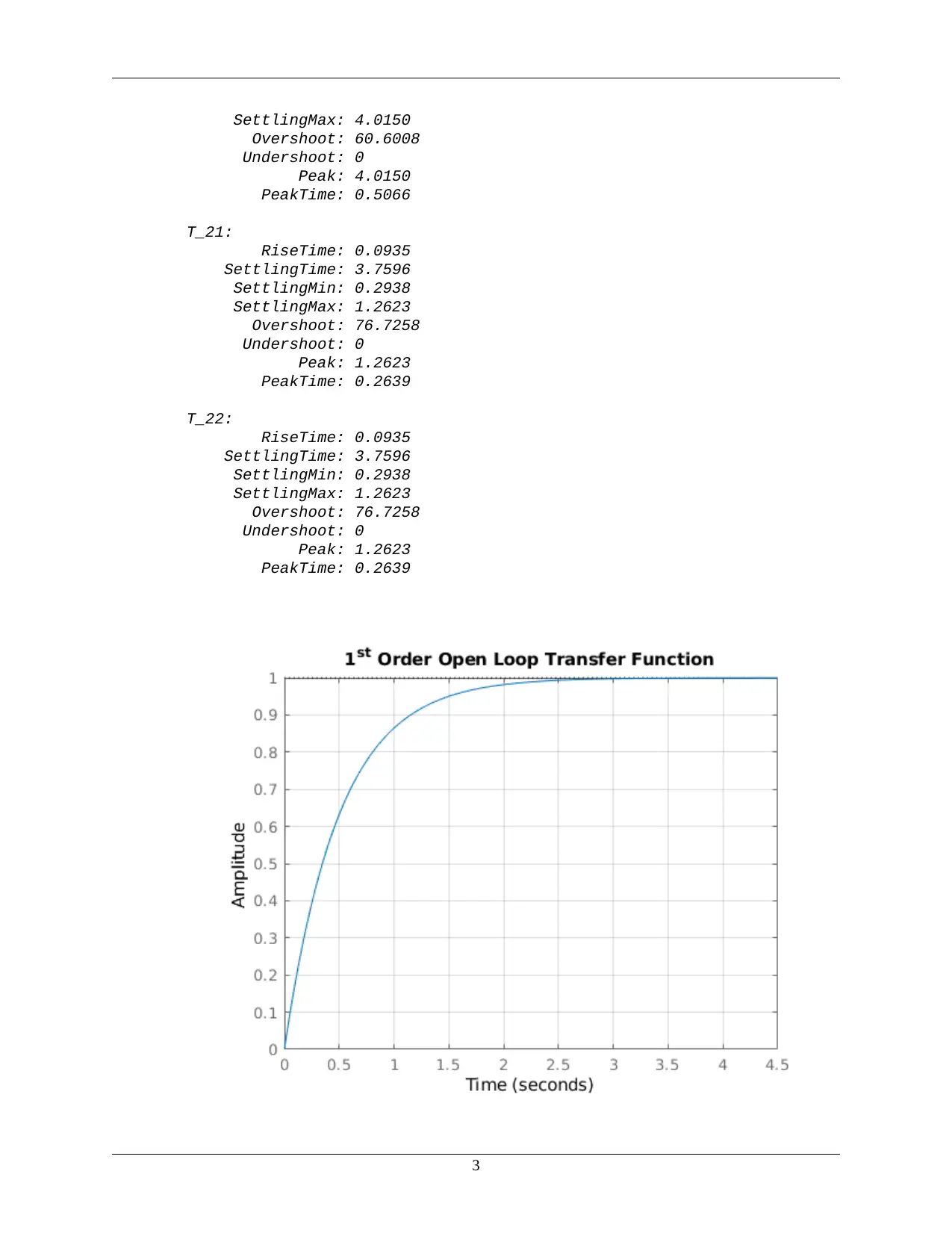
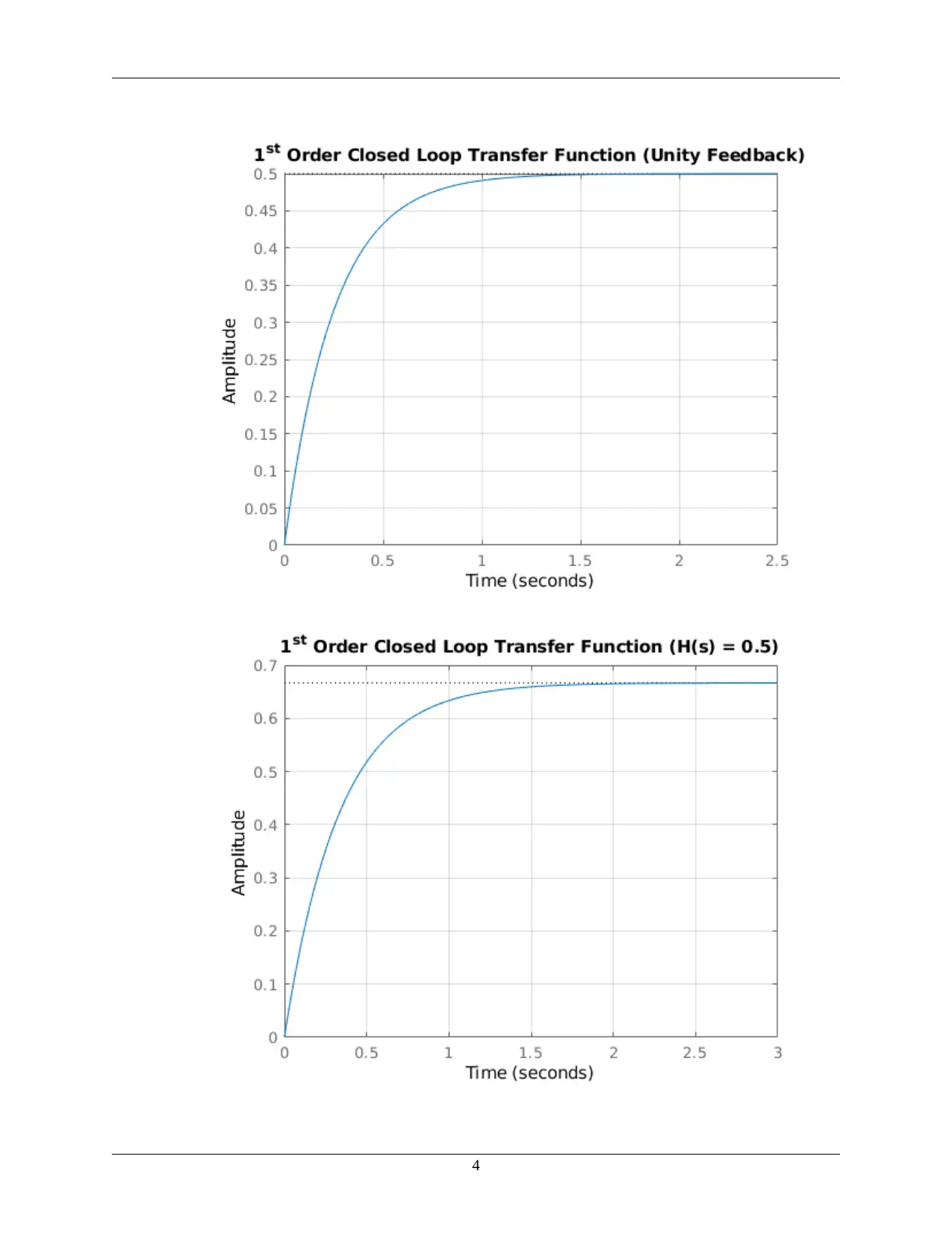
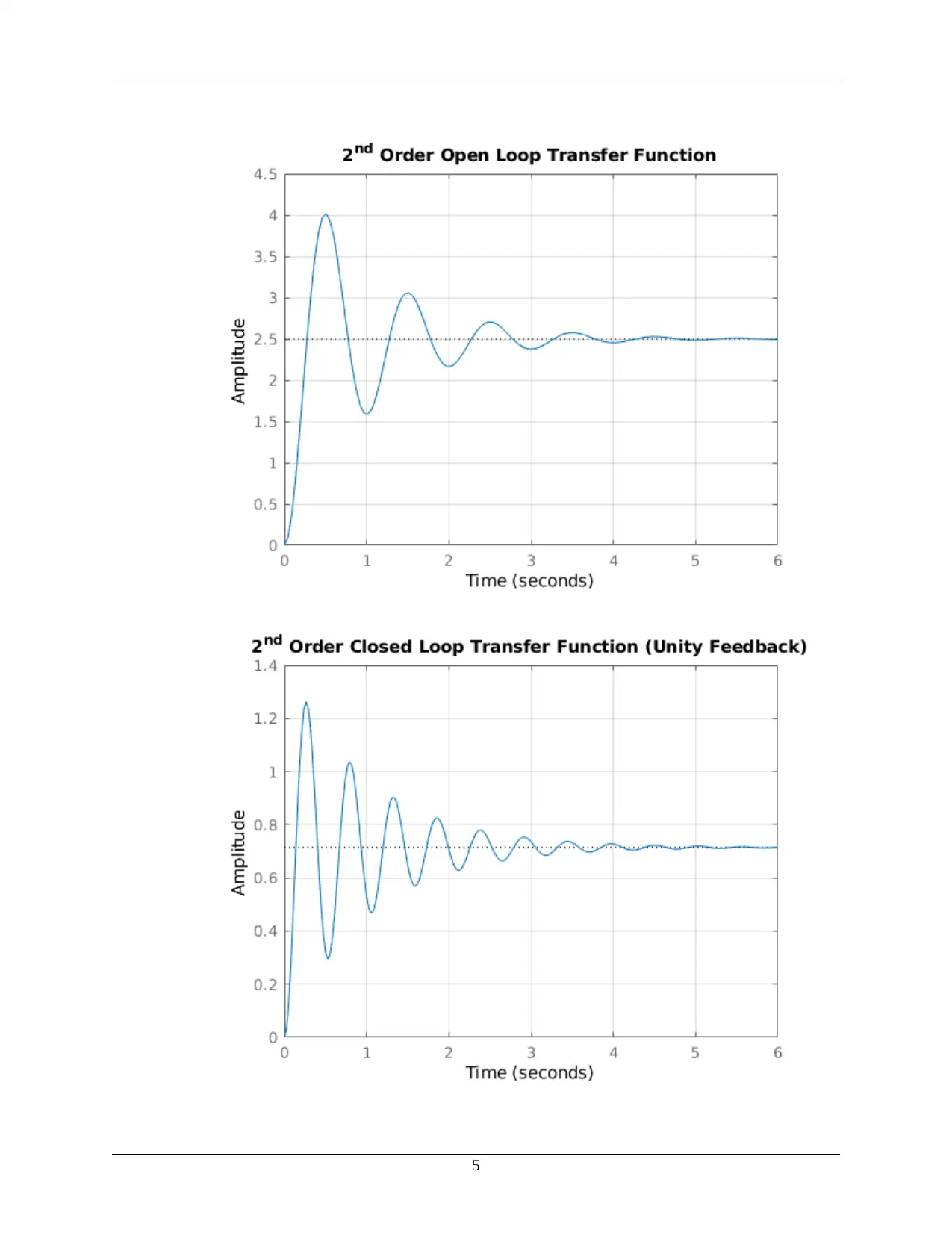
This assignment presents a MATLAB-based solution for analyzing first and second-order control systems. The solution begins by clearing the workspace and defining the s-domain transfer function variable. It then defines and analyzes the open-loop transfer function of a first-order system, plotting its step response and extracting key performance metrics like rise time and settling time. The analysis continues by evaluating the closed-loop transfer function with unity feedback and a feedback gain of 0.5, generating corresponding step responses and performance data. The assignment then proceeds to a second-order system, repeating the open-loop and closed-loop analysis with unity and 0.5 feedback, including plots and performance characteristics. The MATLAB code calculates and displays step response information for each configuration, providing a comprehensive analysis of system behavior under different feedback conditions. The results are saved as images, and the performance metrics are displayed for each transfer function, demonstrating the impact of feedback on system response. The assignment aims to determine the transfer function of first and second order systems from experimental data and analyze the effect of feedback on these systems.

% clear the console, workspace and close all open figures
clc; clear; close all;
% define s variable for s-domain transfer function
s = tf('s');
% Open loop trasfer function (OLTF)
G_1 = 1/(1+0.5*s);
% Step response of OLTF
figure(1);
step(G_1), grid;
title('1^{st} Order Open Loop Transfer Function');
disp('G_1: ');
disp(stepinfo(G_1));
saveas(gcf,'FO_OLTF.png');
% Closed loop transfer function (CLTF) with unity feedback (H(s) = 1)
T_11 = feedback(G_1, 1);
% Step response for unity feedback CLTF
figure(2);
step(T_11), grid;
title('1^{st} Order Closed Loop Transfer Function (Unity Feedback)');
disp('T_11: ');
disp(stepinfo(T_11));
saveas(gcf,'FO_CLTF_Unity.png');
% Closed loop transfer function (CLTF) with H(s) = 0.5
T_12 = feedback(G_1, 0.5);
% Step response for feedback CLTF, H(s) = 0.5
figure(3);
step(T_12), grid;
title('1^{st} Order Closed Loop Transfer Function (H(s) = 0.5)');
disp('T_12: ');
disp(stepinfo(T_12));
saveas(gcf,'FO_CLTF_0.5.png');
% Second order system
G_2 = 101.20/(s^2 + 2*s + 40.48);
% Step response of OLTF
figure(4);
step(G_2), grid;
title('2^{nd} Order Open Loop Transfer Function');
disp('G_2: ');
disp(stepinfo(G_2));
saveas(gcf,'SO_OLTF.png');
% Closed loop transfer function (CLTF) with unity feedback (H(s) = 1)
T_21 = feedback(G_2, 1);
1

% Step response for unity feedback CLTF
figure(5);
step(T_21), grid;
title('2^{nd} Order Closed Loop Transfer Function (Unity Feedback)');
disp('T_21: ');
disp(stepinfo(T_21));
saveas(gcf,'SO_CLTF_Unity.png');
% Closed loop transfer function (CLTF) with H(s) = 0.5
T_22 = feedback(G_2, 0.5);
% Step response for feedback CLTF, H(s) = 0.5
figure(6);
step(T_22), grid;
title('2^{nd} Order Closed Loop Transfer Function (H(s) = 0.5)');
disp('T_22: ');
disp(stepinfo(T_21));
saveas(gcf,'SO_CLTF_Unity.png');
G_1:
RiseTime: 1.0985
SettlingTime: 1.9560
SettlingMin: 0.9045
SettlingMax: 1.0000
Overshoot: 0
Undershoot: 0
Peak: 1.0000
PeakTime: 5.2729
T_11:
RiseTime: 0.5493
SettlingTime: 0.9780
SettlingMin: 0.4523
SettlingMax: 0.5000
Overshoot: 0
Undershoot: 0
Peak: 0.5000
PeakTime: 2.6365
T_12:
RiseTime: 0.7323
SettlingTime: 1.3040
SettlingMin: 0.6030
SettlingMax: 0.6666
Overshoot: 0
Undershoot: 0
Peak: 0.6666
PeakTime: 3.5153
G_2:
RiseTime: 0.1857
SettlingTime: 3.6395
SettlingMin: 1.5835
2

SettlingMax: 4.0150
Overshoot: 60.6008
Undershoot: 0
Peak: 4.0150
PeakTime: 0.5066
T_21:
RiseTime: 0.0935
SettlingTime: 3.7596
SettlingMin: 0.2938
SettlingMax: 1.2623
Overshoot: 76.7258
Undershoot: 0
Peak: 1.2623
PeakTime: 0.2639
T_22:
RiseTime: 0.0935
SettlingTime: 3.7596
SettlingMin: 0.2938
SettlingMax: 1.2623
Overshoot: 76.7258
Undershoot: 0
Peak: 1.2623
PeakTime: 0.2639
3

4

5

Published with MATLAB® R2018b
6