EEE 303A: Comprehensive Solutions for Control Systems Test 1 Problems

This document presents comprehensive solutions to an Electrical Engineering assignment, specifically focusing on control systems. The solutions cover various aspects, including the analysis of Continuous-Time (CT) and Discrete-Time (DT) systems. The assignment requires students to derive ma...Read More

SOLUTIONS: EEE 303A TEST1
Solution 1
Part-1
1.1. H1 ( s ) = ( s+1)
(s+2)( s2 + s+16)
Putting s = jw, we get
H1 ( jw ) = ( jw+ 1)
( jw+ 2)(−w2 + jw +16)
So, magnitude = |H1 ( jw )∨¿ √ (w2+1)
√ (w2+4)√ ((16−w2)+ w2 )
Phase = ∠ H1 ( jw ) =tan−1 w−tan−1 w
2 −¿ tan−1 w
(16−w2) −πu(w2−16)¿
Asymptotic plot:
Asymptotes at corner frequencies of 1 rad/s(20dB/dec, 90deg), 2 rad/s (-20dB/dec, -90deg) and √16
rad/s(-40dB/dec, -180deg)
The transfer function has quadratic terms in the denominator. On comparing the quadratic terms
with the standard form of s2 +2 ξ wn s+ wn
2, we get wn=¿ √16 and ξ= 1
8 =0.125<1. Hence, the
system is underdamped. The asymptotic plot also shows significant resonance.

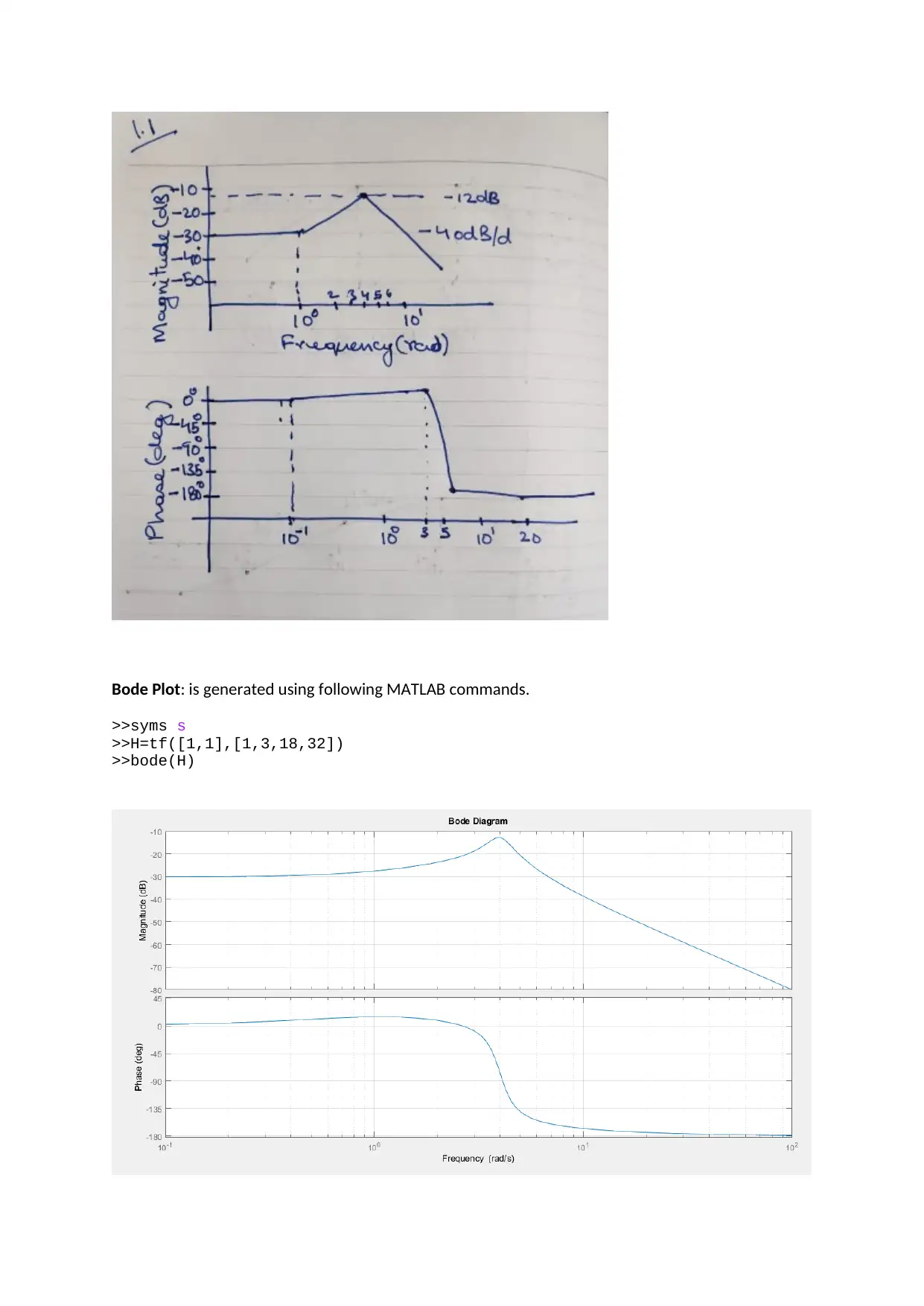
Bode Plot: is generated using following MATLAB commands.
>>syms s
>>H=tf([1,1],[1,3,18,32])
>>bode(H)

1.2. H2 ( s )= s
(s+10)( s+1)
Putting s = jw, we get
H2 ( jw )= jw
( jw+ 10)( jw +1)
So, magnitude = | H2 ( jw ) ∨¿ w
√ (w2+100)√ (w2+1)
Phase = ∠ H2 ( jw ) = π
2 −tan−1 w
10 −¿ tan−1 w ¿
Asymptotic Plot:
Asymptotes at corner frequencies of 1rad/s (-20dB/dec, -90deg), 10rad/s (-20dB/dec, -90deg) and 0
rad/s(20dB/dec, 90deg)
Bode Plot: is generated using following MATLAB commands.
>>syms s

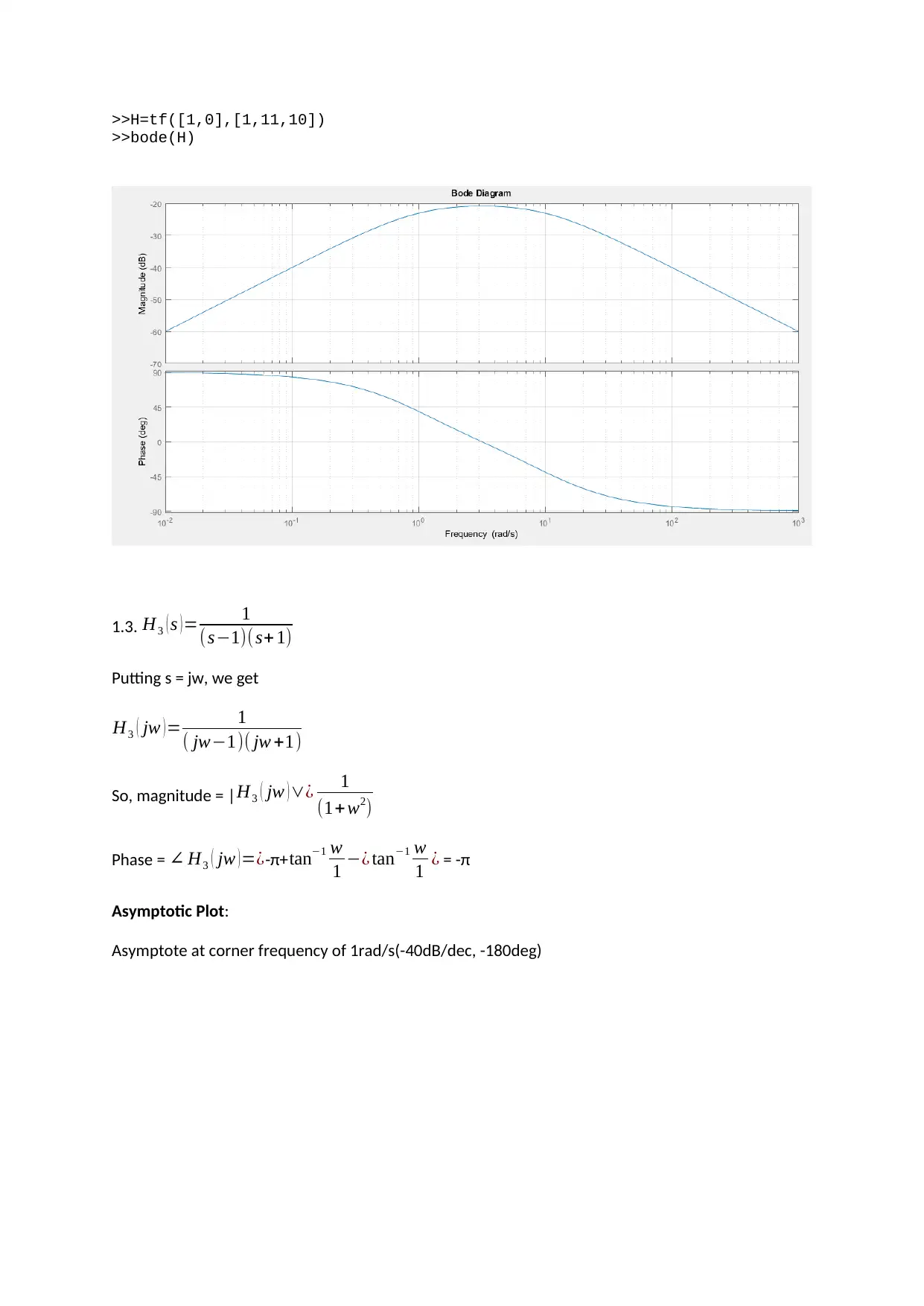
>>H=tf([1,0],[1,11,10])
>>bode(H)
1.3. H3 ( s )= 1
(s−1)( s+ 1)
Putting s = jw, we get
H3 ( jw )= 1
( jw−1)( jw +1)
So, magnitude = |H3 ( jw )∨¿ 1
(1+ w2)
Phase = ∠ H3 ( jw )=¿-π+tan−1 w
1 −¿ tan−1 w
1 ¿ = -π
Asymptotic Plot:
Asymptote at corner frequency of 1rad/s(-40dB/dec, -180deg)

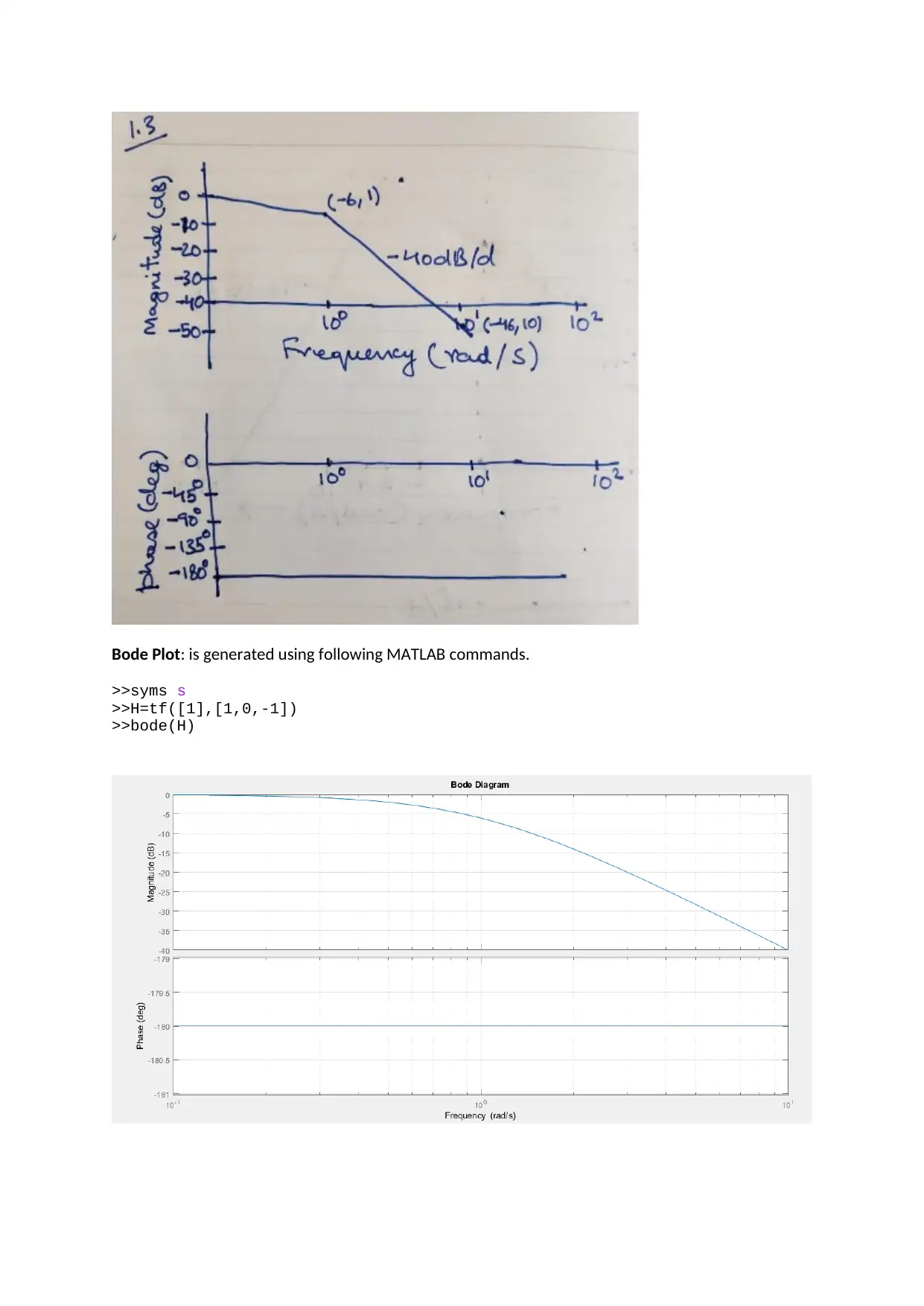
Bode Plot: is generated using following MATLAB commands.
>>syms s
>>H=tf([1],[1,0,-1])
>>bode(H)

1.4. H4 ( s ) = s
(s +1)( s2+ s+16)
Putting s = jw, we get
H4 ( jw ) = jw
( jw +1)(−w2+ jw +16)
So, magnitude = | H4 ( jw ) ∨¿ w
√(w2 +1)√ ((16−w2)+w2)
Phase = ∠ H4 ( jw ) = π
2 −tan−1 w
1 −¿ tan−1 w
( 16−w2 )−πu (w2−16)¿
Asymptotic Plot:
Asymptotes at corner frequencies of 0 rad/s (+20dB/dec, +90deg), 1rad/s (-20dB/dec, -90deg) and
√16 rad/s(-40dB/dec, -180deg)
The transfer function has quadratic terms in the denominator. On comparing the quadratic terms
with the standard form of s2 +2 ξ wn s+ wn
2, we get wn=¿ √16 and ξ= 1
8 =0.125<1. Hence, the
system is underdamped. The asymptotic plot also shows significant resonance.

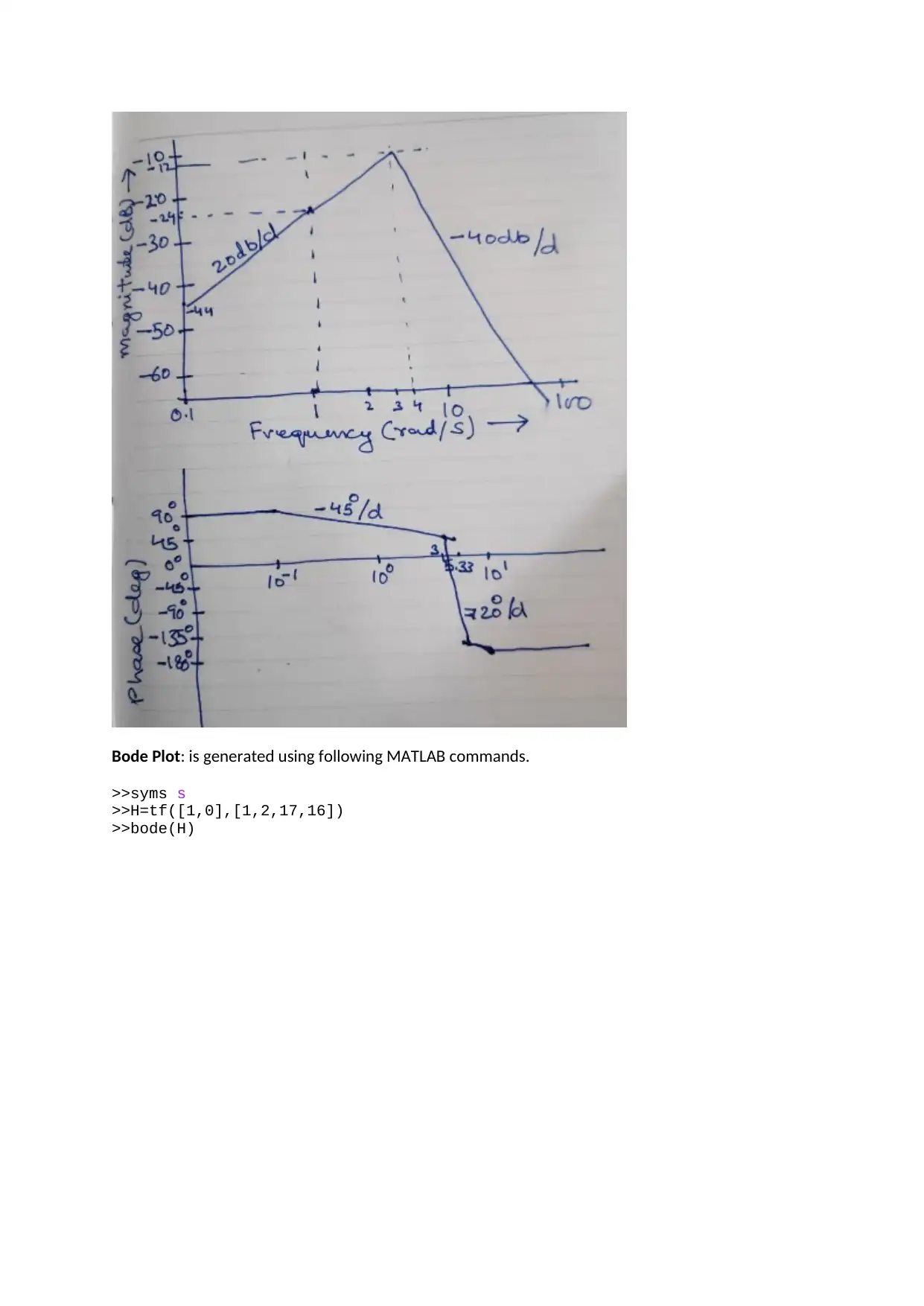
Bode Plot: is generated using following MATLAB commands.
>>syms s
>>H=tf([1,0],[1,2,17,16])
>>bode(H)

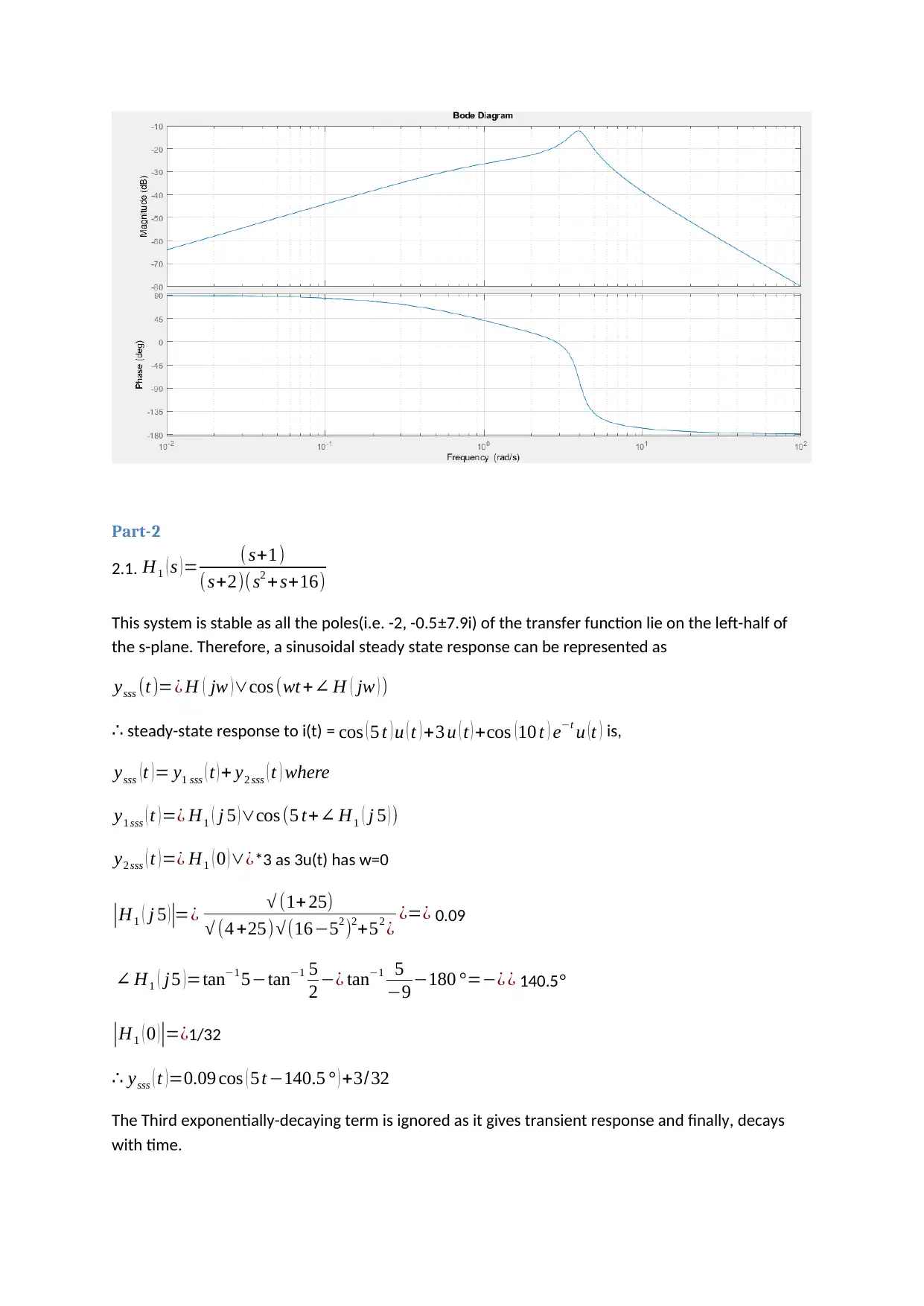
Part-2
2.1. H1 ( s )= ( s+1)
(s+2)( s2 + s+16)
This system is stable as all the poles(i.e. -2, -0.5±7.9i) of the transfer function lie on the left-half of
the s-plane. Therefore, a sinusoidal steady state response can be represented as
ysss (t)=¿ H ( jw ) ∨cos (wt +∠ H ( jw ) )
∴ steady-state response to i(t) = cos ( 5 t ) u ( t ) +3 u ( t ) +cos (10 t ) e−t u (t ) is,
ysss (t )= y1 sss ( t ) + y2 sss ( t ) where
y1 sss ( t ) =¿ H1 ( j 5 ) ∨cos (5 t+∠ H1 ( j 5 ) )
y2 sss ( t ) =¿ H1 ( 0 ) ∨¿*3 as 3u(t) has w=0
|H1 ( j 5 )|=¿ √ (1+ 25)
√ (4 +25)√(16−52 )2+52 ¿ ¿=¿ 0.09
∠ H1 ( j5 )=tan−1 5−tan−1 5
2 −¿ tan−1 5
−9 −180 °=−¿ ¿ 140.5°
|H1 ( 0 )|=¿1/32
∴ ysss ( t ) =0.09 cos ( 5 t −140.5 ° ) +3/32
The Third exponentially-decaying term is ignored as it gives transient response and finally, decays
with time.

2.2. H2 ( s )= s
(s+10)( s+1)
This system is stable as all the poles(i.e. -10, -1) of the transfer function lie on the left-half of the s-
plane. Therefore, a sinusoidal steady state response can be represented as
ysss (t)=¿ H ( jw ) ∨cos (wt +∠ H ( jw ) )
∴ steady-state response to i(t) = cos ( 5 t ) u ( t ) +3 u ( t ) +cos (10 t ) e−t u (t ) is,
ysss ( t ) = y1 sss ( t ) + y2 sss ( t ) where
y1 sss ( t )=¿ H2 ( j 5 )∨cos (5 t+∠ H2 ( j 5 ) )
y2 sss ( t ) =¿ H2 ( 0 ) ∨¿*3 as 3u(t) has w=0
|H2 ( j 5 )|=¿ 5
√ (100+25)√(1+25)=¿ 0.087, ∠ H2 ( j5 ) =90 °−tan−1 5
10 −tan−1 5
1 = -15°
|H2 ( 0 )|=¿0
∴ ysss ( t ) =0.087 cos ( 5 t−15 ° )
2.3. H3 ( s )= 1
(s−1)( s+ 1)
This system is unstable as one of the poles(i.e. s =+1) of the transfer function lies on the right-half of
the s-plane. Therefore, a steady state response is not well-defined.
2.4. H4 ( s ) = s
(s +1)( s2+ s+16)
This system is stable as all the poles(i.e. -1, -0.5±7.9i) of the transfer function lie on the left-half of
the s-plane. Therefore, a sinusoidal steady state response can be represented as
ysss (t)=¿ H ( jw ) ∨cos (wt +∠ H ( jw ) )
∴ steady-state response to i(t) = cos ( 5 t ) u ( t ) +3 u ( t ) +cos (10 t ) e−t u (t ) is,
ysss (t )= y1 sss ( t ) + y2 sss ( t ) where
y1 sss ( t ) =¿ H4 ( j5 ) ∨cos( 5t +∠ H4 ( j 5 ) )
y2 sss ( t )=¿ H4 ( 0 )∨¿*3 as 3u(t) has w=0
|H 4 ( j 5 )|=¿ 5
√ (1+ 25)√ (16−52 )2+52 ¿ ¿=¿ 0.095
∠ H1 ( j5 ) =90 ° −tan−1 5−¿ tan−1 5
−9 −180 °=−140 ° ¿

|H 4 ( 0 )|=¿0
∴ ysss ( t ) =0.095 cos ( 5 t−140 ° )
Solution 2
Part-1
1.1. H1 ( z ) = z
(z−0.5)( z−0.7)
Putting z = e j Ω, we get
H1 ( e j Ω ) = e j Ω
(e j Ω −0.5)(e j Ω −0.7) = cos Ω+ jsinΩ
(cos Ω−.5+ jsinΩ)(cos Ω−.7+ jsinΩ)
So, magnitude = | H1 ( e j Ω ) ∨¿ 1
√ (cos Ω−.5)2 +(sinΩ)2
√ (cos Ω−.7)2+(sinΩ)2
Phase = ∠ H1 ( e j Ω ) =Ω−tan−1 sinΩ
(cos Ω−.5) −tan−1 sinΩ
(cos Ω−.7) + Lπ
(L: add π whenever denominator of tan−1 num
den is negative ¿
Asymptotic Plot:
Approximate asymptotes are drawn at the corner frequencies of the transformation z = 1 + s for
roots near 1. The asymptotes are valid until about one decade below 3.14 (Nyquist frequency).
Asymptotes at corner frequencies of 0.5 rad/s (-20dB/dec, -90deg) and 0.3 rad/s(-20dB/dec, -90deg);
the second one is close to the limit of validity of our approximation, but the first is clearly beyond it.

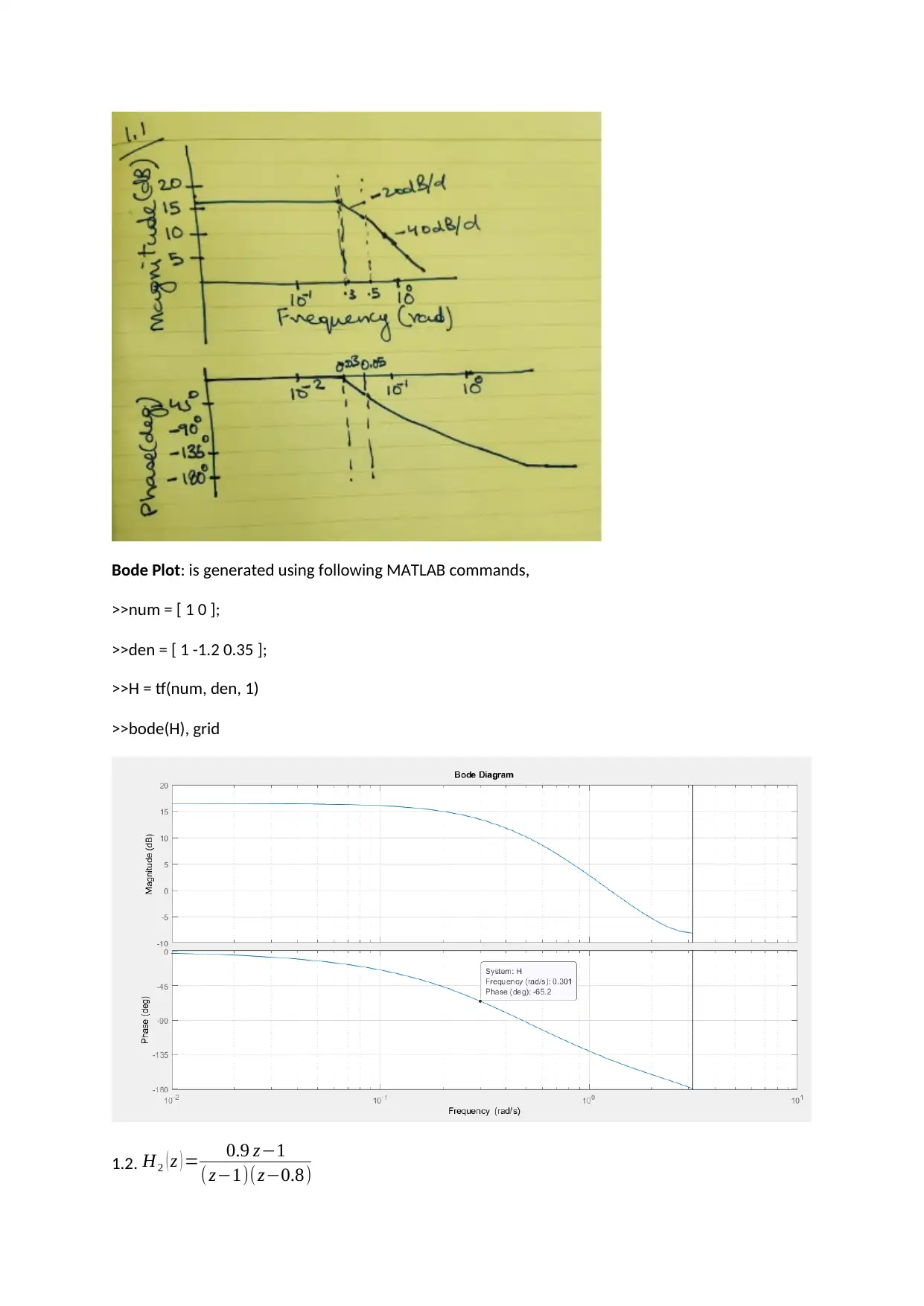
Bode Plot: is generated using following MATLAB commands,
>>num = [ 1 0 ];
>>den = [ 1 -1.2 0.35 ];
>>H = tf(num, den, 1)
>>bode(H), grid
1.2. H2 ( z ) = 0.9 z−1
( z−1)(z−0.8)

Putting z = e j Ω, we get
H2 (e j Ω ) = 0.9 e j Ω−1
(e j Ω −1)(e j Ω−0.8) = 0.9 cos Ω+ j 0.9 sinΩ−1
( cos Ω−1+ jsinΩ)(cos Ω−.8+ jsinΩ)
So, magnitude = | H2 ( e j Ω ) ∨¿ √ (0.9 cos Ω−1)2 +(0.9 sinΩ)2
√( cos Ω−1)2 +( sinΩ)2
√ (cos Ω−.8)2 +(sinΩ)2
Phase = ∠ H2 ( e j Ω ) =tan−1 0.9 sinΩ
(0.9 cos Ω−1)−tan
−1 sinΩ
(cos Ω−1) −tan−1 sinΩ
(cos Ω−.8) + Lπ
(L: add π whe never denominator of tan−1 num
den is negative ¿
Asymptotic Plot:
Asymptotes at corner frequencies of 0rad/s, (-20dB/dec, -90deg), 0.11rad/s (+20dB/dec, -90deg)
and 0.2 rad/s(-20dB/dec, -90deg)
Bode Plot: is generated using following MATLAB commands,

>>num = [ 0.9 -1 ];
>>den = [ 1 -1.8 0.8 ];
>>H = tf(num, den, 1)
>>bode(H), grid
1.3. H3 ( z )= 1
(0.5 z−1)( z+ 0.7)
Putting z = e j Ω, we get
H3 ( e j Ω ) = 1
(0.5 e j Ω −1)(e j Ω +0.7) = 1
(0.5 cos Ω−1+ j 0.5 sinΩ)(cos Ω+0.7+ jsinΩ)
So, magnitude = | H3 ( e j Ω ) ∨¿ 1
√ (0.5 cos Ω−1)2 +(0.5 sinΩ)2
√( cos Ω+0.7)2 +( sinΩ)2
Phase = ∠ H3 ( e j Ω ) =−tan−1 0.5 sinΩ
( 0.5cos Ω−1) −tan
−1 sinΩ
(cos Ω+0.7) + L π
(L: add π whenever denominator of tan−1 num
den is negative ¿
Asymptotic Plot:
Asymptotes at corner frequencies of 2, (-20dB/dec, +90deg), clearly beyond the range of our
approximation; the other corner frequency at 0.7 does not satisfy the approximation assumptions
(because of “ringing”). The approximation is only good at DC and “low frequencies” where the
transfer function is approximately constant.

Bode Plot: is generated using following MATLAB commands,
>>num = [ 1 ];
>>den = [ 0.5 -0.65 -0.7 ];
>>H = tf(num, den, 1)
>>bode(H), grid
1.4. H4 ( z ) = z −1
(z −0.9)(z2 −1.8 z +0.9)
Putting z = e j Ω, we get
H4 ( e j Ω )= e j Ω−1
( e j Ω−0.9)( e j 2 Ω−1.8 e j Ω +0.9) = cos Ω−1+ jsinΩ
(cos Ω−0.9+ jsinΩ)(cos 2 Ω−1.8 cosΩ+0.9+ j(sin 2 Ω−1.8 sinΩ))
So, magnitude = |
H4 ( e j Ω )∨¿ √ (cos Ω−1)2+(sinΩ)2
√ (cos Ω−0.9)2 +( sinΩ)2
√ (cos 2 Ω−1.8 cosΩ+0.9)2 +(sin 2 Ω−1.8 sinΩ)2
Phase =
∠ H4 ( e j Ω ) =tan−1 sinΩ
(cos Ω−1)−tan
−1 sinΩ
(cos Ω−0.9) −tan−1 (sin 2 Ω−1.8 sinΩ)
(cos 2 Ω−1.8 cosΩ+0.9) + L π
(L: add π whenever de nominator of tan−1 num
den is negative ¿
Asymptotic Plot:

Asymptotes at corner frequencies of 0, (20dB/dec, +90deg), 0.1, (-20dB/dec, -90deg), √(0.1) = 0.316
(-40dB/dec, - 180deg). 0.316 is the natural frequency of the quadratic term after the conversion z =
1+s. It is near the limit of validity of our approximation.
Bode Plot: is generated using following MATLAB commands,
>>num = [ 1 -1 ];
>>den = [ 1 -2.7 2.52 -0.81 ];
>>H = tf(num, den, 1)
>>bode(H), grid
Part-2
2.1 . H1 ( z )= z
( z−0.5)(z −0.7)
This system is stable as all its poles(|z|=0.5, 0.7 < 1) lie within the unit circle.
If the input is i(n) = sin(0.1n)u(n-10)+2u(n), then, steady state response would also be a sinusoid
given by,
yss (n) = |H1 ( e j 0.1 )∨¿sin(0.1n+∠ H1 ( e j 0.1 ) ¿ + 2*|H1 ( e j 0=1 ) ∨¿
| H1 ( e j 0.1 ) ∨¿ 1
√ (cos 0.1−.5)2+ ( sin 0.1 ) 2
√ ( cos 0.1−.7)2 + ( sin 0.1 ) 2 =6.36

Phase = ∠ H1 ( e j 0.1 )=0.1−tan−1 sin0.1
( cos 0.1−.5) −tan−1 sin 0.1
(cos 0.1−.7)=−24 °
|H1 ( e j 0=1 ) ∨¿ 1
√ ( 1−.5 )2
√ ( 1−.7 )2 = 1
0.5∗0.3 =6.67
Therefore,
yss (n) = 6.36sin(0.1n −24 ° ¿ + 13.3
2.2. H2 ( z ) = 0.9 z−1
( z−1)(z−0.8)
As one of the poles lie on the unit circle, the system is unstable. Therefore, the steady state response
is not well-defined.
2.3. H3 ( z )= 1
(0.5 z−1)( z+ 0.7) = 1
0.5 (z−2)( z+0.7)
Here, the poles of this transfer function are z = 2, -0.7. Since one of the poles lies outside the unit
circle, hence, the system is unstable and so, the steady state response is not well-defined.
2.4 . H4 ( z )= z−1
( z −0.9)( z2 −1.8 z +0.9)
This system is stable as all its poles(|z|=0.9, 0.9±j0.3) lie within the unit circle.
If the input is i(n) = sin(0.1n)u(n-10)+2u(n), then, steady state response would also be a sinusoid
given by,
yss (n) = | H4 ( e j 0.1 ) ∨¿sin(0.1n+∠ H4 ( e j 0.1 ) ¿ + 2*| H4 ( e j 0=1 ) ∨¿
|
H4 ( e j 0.1 )∨¿ √( cos 0.1−1)2+(sin 0.1)2
√(cos 0.1−0.9)2+(sin 0.1)2
√(cos 0.2−1.8 cos 0.1+0.9)2 +( sin 0.2−1.8 sin 0.1)2 =¿
7.97
Phase =
∠ H4 ( e j 0.1 ) =tan−1 sin 0.1
(cos 0.1−1)−tan
−1 sin 0.1
(cos 0.1−0.9)−tan−1 (sin 0.2−1.8 sin 0.1)
(cos 0.2−1.8 cos 0.1+ 0.9) +π=34.4 °
|H1 ( e j 0=1 ) ∨¿ 0
Therefore,
yss (n) = 7.97sin(0.1n +34.4 ° ¿

Solution 3
Let us generate a normalized 2nd order high-pass Butterworth CT filter (assuming ωc=1 rad /s) using
MATLAB commands:
>>[b, a] = butter(2, 1, ‘high’, ‘s’)
>>sys = tf(b, a)
It will give transfer function as:
H ( s ) = s2
s2 +1.414 s +1
And corresponding Bode plot can be generated using matlab command:
>> bode(sys)
As can be seen from above plot, the attenuation of -40 db is achieved at frequencies less than0.1 ωc.
Value of 0.1 ωc = 1 Hz (given) ¿> ωc= 2 π ×1
0.1 =68.2 rad / s
Replace s with s=s /ωc in the above transfer function, we get the transfer function of 2nd-order
high-pass Butterworth CT filter with cutoff frequency ωc :
H ( s )= s2
s2 +88.799 s+3943.83
Using MATLAB we find out phase and magnitude of the transfer function at
10 Hz=¿ ω=2 π ×10=62.8 rad /s:
MATLAB code:
>> syms s
>> H=tf([1,0,0],[1,88.799,3943.83])
>>[m,p]=bode(H,62.8)

We get m=0.707, the amplitude distortion is 1-m=0.293 or -10.6626dB. This will be maximum
distortion and all other frequencies will be distorted less. This can also be verified from below Bode
plot of function H.
Solution 4
The first order transfer function of low pass filter can be characterized by equation,
H ( z )= a
z −(1−a)
Since we are sampling at frequency 20kHz ¿>T = 1
20000 =0.5e-3 seconds, the discrete frequency is
Ω=ωT.
We need to evaluate the magnitude of above mentioned transfer function at the highest frequency
which will be frequency of the maximum distortion,
H |e j Ω
|= a
√ ¿ ¿ ¿ ¿
We can solve this inequality analytically (find the smallest “a” that satisfies the inequality) or
numerically by iterating the bode function evaluations:
MATLAB code:
>>omega = pi*0.001;
>>min_a = 0.1;
>>for a = omega:0.0001:0.1
>> m = bode(tf(a, [1 -(1-a)], 1), omega);
>> if m > 0.99
>> if a < min_a
>> min_a = a;
>> end
>> end

>>end
>>min_a
>>m = bode(tf(min_a, [1 -(1-min_a)], 1), 0.314)
>>20*log10(m)
We find, minimum value of a = 0.022 and magnitude of transfer function as 0.071 or -23dB. The
transfer function with a = 0.022, will be H ( z ) = 0.022
z −0.978
We verify this by plotting Bode plot using MATLAB.
MATLAB code:
>>num = [ 0.022 ];
>>den = [ 1 -0.978 ];
>>H = tf(num, den, 0.0005)
>>bode(H), grid