Newton's Law of Cooling: An Experimental Investigation & Data Analysis

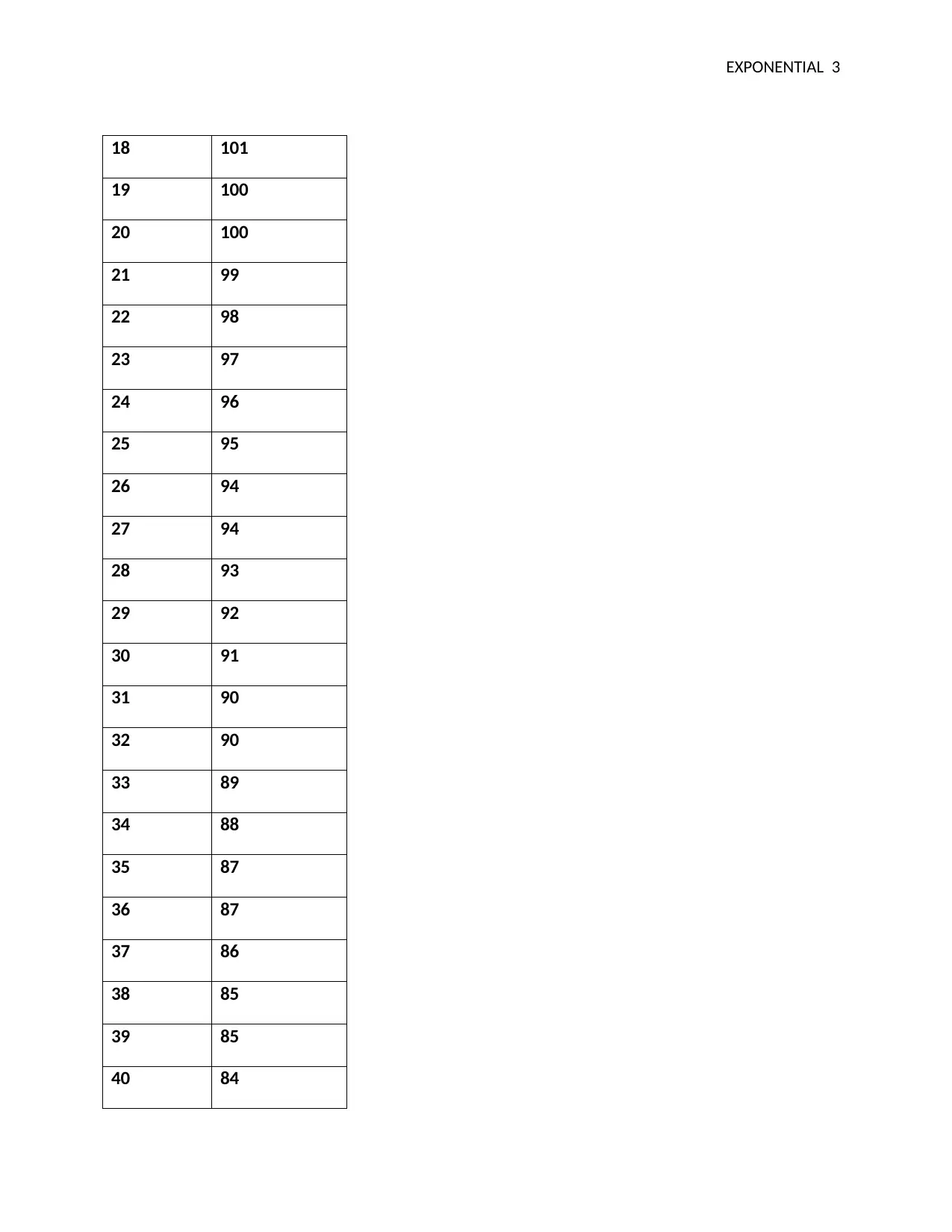
This assignment focuses on understanding exponential decay through an experiment based on Newton's Law of Cooling, which states that the rate of temperature change of an object is proportional to the difference between its temperature and the ambient temperature. The experiment involved measuring the temperature of a liquid over time as it cooled, with an ambient temperature of 19°C. The data collected was used to create a scatterplot and analyze the cooling process. The analysis involved using differential equations and integration methods to derive equations for predicting the temperature at any given time. The growth constant 'k' was calculated, and the time needed for the object to cool to half its initial temperature difference was determined. The relationship between the growth constant and half-life was also explored. The study concludes by demonstrating the application of the derived equations and discussing the assumption of conductive heat exchange in the experiment, and the student can find similar solved assignments and study resources on Desklib.

EXPONENTIAL 1
NAME OF STUDENT:
STUDENT NUMBER: 170830H
INSTITUTION AFFILIATION:

EXPONENTIAL 2
OBJECTIVE:
To build understanding of the exponential decay through an experiment using the Newton's Law of Cooling
INTRODUCTION
The main aim of the experiment was to determine and understand the concept of exponential
growth using Newtons law of cooling which states that the rate of change of temperature of an’
object is proportional to the difference between its own temperature and the ambient
temperature. The temperature of a given surrounding is known as ambient temperature. In our
case, the ambient temperature is 19⁰ c.
So an experiment on the Newtons law of cooling was carried out and the results were obtained’
and a scatterplot was determined as follows:
RESULTS
Time t in
Min
utes
Liquid
Temper
ature in
°C of
T(t) at
time t
9 110
10 109
11 108
12 107
13 106
14 105
15 104
16 103
17 102

EXPONENTIAL 3
18 101
19 100
20 100
21 99
22 98
23 97
24 96
25 95
26 94
27 94
28 93
29 92
30 91
31 90
32 90
33 89
34 88
35 87
36 87
37 86
38 85
39 85
40 84

EXPONENTIAL 4
41 83
42 82
43 82
44 81
45 80
46 80
47 79
48 78
49 78
50 77
51 77
52 76
53 75
54 75
55 74
56 74
57 73
58 72
59 72
60 71
61 71
62 70
63 70

EXPONENTIAL 5
64 69
65 68
66 68
67 67
68 67
69 66
70 66
71 65
72 65
73 64
74 64
75 63
76 63
77 62
78 62
79 62
80 61

EXPONENTIAL 6
DISCUSSION/CONCLUSION
2. Newtons law of cooling depicts that’
    a
d T t k T t T
dt    
where T(t) = temp of objects at any time t,
Ta = ambient temp,
k = growth constant
3. We will use the differential equation to come up with an equation to obtain the temperature at any
time by a method known as integration or by a mehod of separable variables.
(i) Using integration method, The resulting equation therefore has the form Y=Y 0e-k.T(t)-T which is derived
as :
dT/dt=k(T-Ta)

EXPONENTIAL 7
dT/dt-KT=-kTa
IF=eintegral of -kdt = e-kt
e-kt.Y = integral of e-kt. 0dt = 0+c+Ye-kt
So Y=Y0e-kt+c
Where Y= L, Y0=initial temperature change=B-S
So introducing the new terms; L-(B-S)e-k.t + C
Where C=Ta=S
So L=(B-S)e-k.t +S
Introducing an equation with zero equivalent; L-(B-S)e-k.t – S=0
where L = temp of liquid at any time,
S = temp of surroundings,
Y = temp of the liquid – temp of the surroundings.
B = initial temp of the liquid
(ii) Using the method of separable variables, the temperature difference at t=0 and the model is Y 0 =L
S.–
Where L is the temperature of theliuid at time t, S is the temperature of the sorroundings, Y is the
difference between the temperature of the liquid and the sorroundings.
The assumption made was that there was no convective heat exchange but rather only conductive heat
exchange due to temperature difference between the liquid and the sorrounding
The final equation of the model is B-S)e-k.t +S=L

EXPONENTIAL 8
(ii) Where now B is initial temperature of the liquid= 110°C
(i)t t=80 minutes, L=61°C, B=110°C, S=19°C and using these values and the equation
above to calculate the value of k: 61-(110-19)e-80.k 19=0–
So the growth constant k=0.00966
4. Time needed to cool the object to half its initial temperature difference
Initial temperature difference is 110-19=91
Its half is 45.5
= 45.5-91e-0.00966t - 19=0
26.5=91e-0.00966t
The value of t here is then 127 minutes
5. Showing that kThalftime = ln2
k=0.00966
T here is127 minutes
Thalftime=127/2=63.5
kT then= 0.00966x63.5= 0.6341 which is almost equivalent to ln2
6. B-S)e-k.t +S=L So when we double the time and half the time of growth decay gives:
L-(110-19)e-160x0.00966/2 -19=0
L=91x0.4615 +19
L=61
So doubling the time and the half time of growth decay gives the same value of L

EXPONENTIAL 9
7. Using both equations, the liquid temperature remains the same, i.e no cooling takes place.