Corporate Finance Assignment: Analyzing Risk, Return, and Portfolios
VerifiedAdded on 2021/11/13
|5
|903
|22
Homework Assignment
AI Summary
This assignment delves into fundamental concepts in corporate finance, examining the relationship between risk and return in stock investments. It explores the use of standard deviation to quantify risk and its implications for investment decisions, particularly in normally distributed return scenarios. The assignment also addresses portfolio diversification, explaining how adding new stocks can reduce overall portfolio risk based on correlation coefficients. Finally, it provides a mathematical analysis of portfolio risk involving a risk-free asset, demonstrating how the portfolio's risk is influenced by the weight and risk of the risky asset. The assignment draws on established financial literature to support its analysis, offering insights into key financial management principles.

CORPORATE FINANCE
STUDENT ID:
[Pick the date]
STUDENT ID:
[Pick the date]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
CORPORATE FINANCE
PART 1
Question 1
With regards to any stock, two defining characteristics are risk and return. The risk inherent
in the share is on account of movement of the share price owing to which there is variation in
the share returns in different time periods (Damodaran, 2015). This is essentially represented
through standard deviation which highlights the extent of return values dispersion about the
average returns. Thus, if the dispersion of returns is high about the average returns, then it
would lead to higher standard deviation which would imply higher risk associated with the
underlying share (Brealey, Myers. & Allen, 2014).
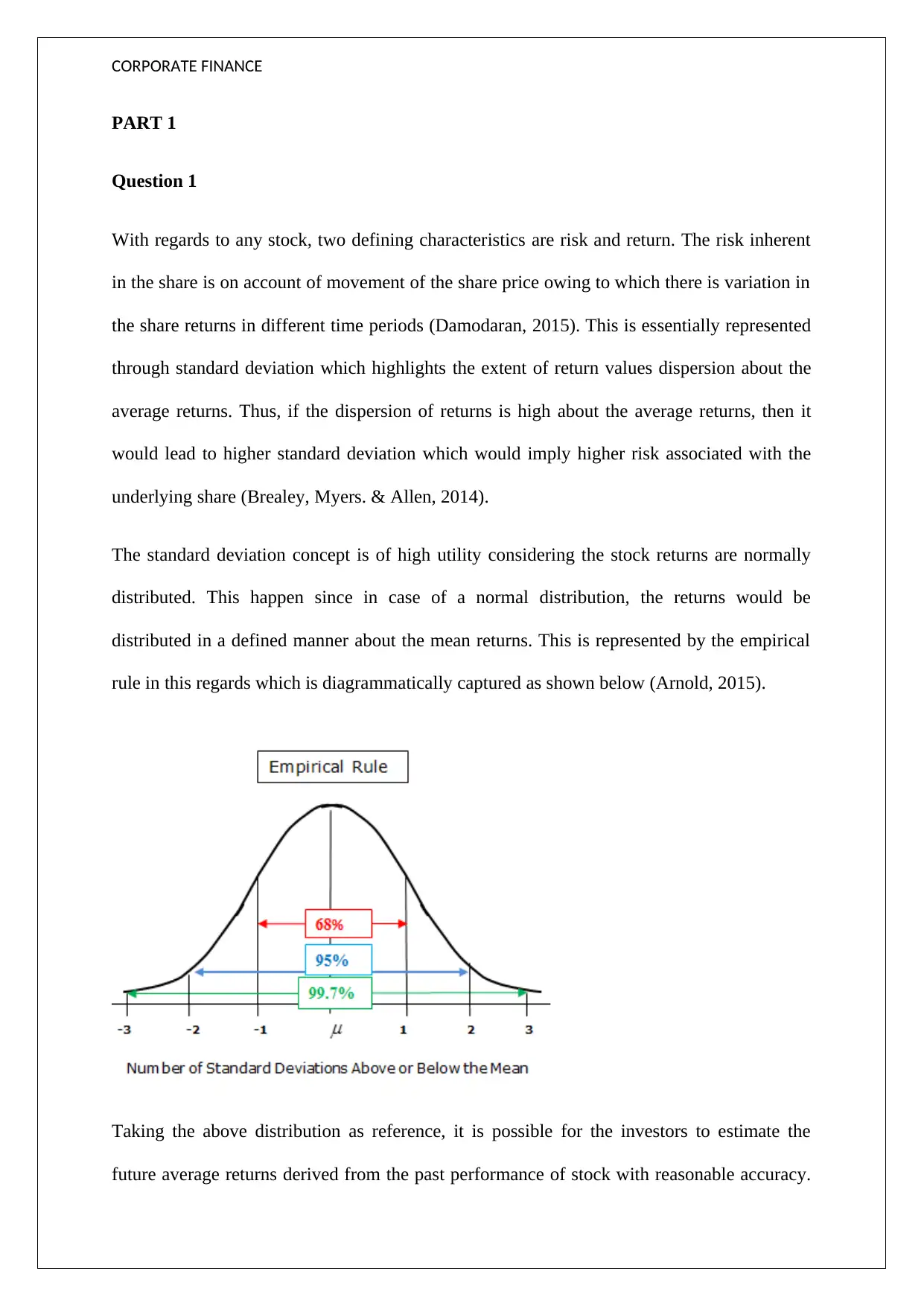
The standard deviation concept is of high utility considering the stock returns are normally
distributed. This happen since in case of a normal distribution, the returns would be
distributed in a defined manner about the mean returns. This is represented by the empirical
rule in this regards which is diagrammatically captured as shown below (Arnold, 2015).
Taking the above distribution as reference, it is possible for the investors to estimate the
future average returns derived from the past performance of stock with reasonable accuracy.
PART 1
Question 1
With regards to any stock, two defining characteristics are risk and return. The risk inherent
in the share is on account of movement of the share price owing to which there is variation in
the share returns in different time periods (Damodaran, 2015). This is essentially represented
through standard deviation which highlights the extent of return values dispersion about the
average returns. Thus, if the dispersion of returns is high about the average returns, then it
would lead to higher standard deviation which would imply higher risk associated with the
underlying share (Brealey, Myers. & Allen, 2014).
The standard deviation concept is of high utility considering the stock returns are normally
distributed. This happen since in case of a normal distribution, the returns would be
distributed in a defined manner about the mean returns. This is represented by the empirical
rule in this regards which is diagrammatically captured as shown below (Arnold, 2015).
Taking the above distribution as reference, it is possible for the investors to estimate the
future average returns derived from the past performance of stock with reasonable accuracy.

CORPORATE FINANCE
Besides, it is also possible to determine the underlying probability of obtaining a particular
value of average return based on empirical stock performance. As a result, decision making is
tremendously aided using the concept of standard deviation and normal distribution of returns
(Petty et. al., 2015).
Question 2
The impact of the addition of new stock in the portfolio can be understood in the backdrop of
diversification theory. Diversification of the portfolio typically reduces the risk of the
portfolio as the stocks may tend to act as natural hedges against the movement of each other
and thereby limit extreme movements in portfolio return in either direction (Parrino &
Kidwell, 2014). However, this would essentially be dependent on the underlying correlation
between the returns of the inserted stock returns .and previous stock returns. In order to
understand this further, reference to mathematical formula for portfolio risk for a portfolio
comprising of two assets is essential (Damodaran, 2015).
The correlation coefficient is indicated by P1,2 while the portfolio risk is captured by the
standard deviation of portfolio returns. It is evident that if the correlation coefficient is
negative, there would be a significant decline in the portfolio risk. This would arise on
account of movements in stock being in opposite direction and thereby reducing the variation
in the portfolio returns (Parrino & Kidwell, 2014). However, to some extent this is also
exhibited in case of positive correlation especially if the magnitude is low. Formation of
diversified portfolio is preferred in comparison to individual stocks as typically these lead to
generation of higher returns for unit assumption of risk which essentially is the objective in
accordance with modern portfolio theory (Brealey, Myers. & Allen, 2014).
Besides, it is also possible to determine the underlying probability of obtaining a particular
value of average return based on empirical stock performance. As a result, decision making is
tremendously aided using the concept of standard deviation and normal distribution of returns
(Petty et. al., 2015).
Question 2
The impact of the addition of new stock in the portfolio can be understood in the backdrop of
diversification theory. Diversification of the portfolio typically reduces the risk of the
portfolio as the stocks may tend to act as natural hedges against the movement of each other
and thereby limit extreme movements in portfolio return in either direction (Parrino &
Kidwell, 2014). However, this would essentially be dependent on the underlying correlation
between the returns of the inserted stock returns .and previous stock returns. In order to
understand this further, reference to mathematical formula for portfolio risk for a portfolio
comprising of two assets is essential (Damodaran, 2015).
The correlation coefficient is indicated by P1,2 while the portfolio risk is captured by the
standard deviation of portfolio returns. It is evident that if the correlation coefficient is
negative, there would be a significant decline in the portfolio risk. This would arise on
account of movements in stock being in opposite direction and thereby reducing the variation
in the portfolio returns (Parrino & Kidwell, 2014). However, to some extent this is also
exhibited in case of positive correlation especially if the magnitude is low. Formation of
diversified portfolio is preferred in comparison to individual stocks as typically these lead to
generation of higher returns for unit assumption of risk which essentially is the objective in
accordance with modern portfolio theory (Brealey, Myers. & Allen, 2014).
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

CORPORATE FINANCE
.Question 3
The variance for a two asset portfolio is found on the basis of the formula shown below.
It is known that one of the asset associated with the portfolio above is a risk free asset. The
word risk free asset would imply no risk and considering that standard deviation tends to be
used as a measure of risk, hence standard deviation associated with the returns of a risk free
asset would be zero (Petty et. al., 2015). The mathematical computation in this regards are
carried out below.
Consider asset 1 as the risk free asset and hence σ1 =0. Hence, the portfolio risk can be
reduced to the following.
σp2 = w12*02 + w22*σ22 + 2w1w2 P1,2 σ2*0
The first and third term in the expression above would reduce to zero.
Hence, σp2 = w22σ22
Taking the square root of both sides, we get
σp = w2σ2
Thus, it is apparent for a two asset portfolio with one asset as the risk free asset, the portfolio
risk would be dependent on the weight of the risky asset and the underlying risk associated
with the risky asset denoted by the respective standard deviation (Damodaran, 2015).
.Question 3
The variance for a two asset portfolio is found on the basis of the formula shown below.
It is known that one of the asset associated with the portfolio above is a risk free asset. The
word risk free asset would imply no risk and considering that standard deviation tends to be
used as a measure of risk, hence standard deviation associated with the returns of a risk free
asset would be zero (Petty et. al., 2015). The mathematical computation in this regards are
carried out below.
Consider asset 1 as the risk free asset and hence σ1 =0. Hence, the portfolio risk can be
reduced to the following.
σp2 = w12*02 + w22*σ22 + 2w1w2 P1,2 σ2*0
The first and third term in the expression above would reduce to zero.
Hence, σp2 = w22σ22
Taking the square root of both sides, we get
σp = w2σ2
Thus, it is apparent for a two asset portfolio with one asset as the risk free asset, the portfolio
risk would be dependent on the weight of the risky asset and the underlying risk associated
with the risky asset denoted by the respective standard deviation (Damodaran, 2015).
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

CORPORATE FINANCE
References
Arnold, G. (2015) Corporate Financial Management. 3rd ed. Sydney: Financial Times
Management.
Brealey, R. A., Myers, S. C. & Allen, F. (2014) Principles of corporate finance, 6th ed. New
York: McGraw-Hill Publications
Damodaran, A. (2015). Applied corporate finance: A user’s manual 3rd ed. New York:
Wiley, John & Sons.
Parrino, R. & Kidwell, D. (2014) Fundamentals of Corporate Finance, 3rd ed. London:
Wiley Publications
Petty, J.W., Titman, S., Keown, A., Martin, J.D., Martin, P., Burrow, M. & Nguyen, H. (2015).
Financial Management, Principles and Applications, 6th ed.. NSW: Pearson Education,
French Forest Australia
References
Arnold, G. (2015) Corporate Financial Management. 3rd ed. Sydney: Financial Times
Management.
Brealey, R. A., Myers, S. C. & Allen, F. (2014) Principles of corporate finance, 6th ed. New
York: McGraw-Hill Publications
Damodaran, A. (2015). Applied corporate finance: A user’s manual 3rd ed. New York:
Wiley, John & Sons.
Parrino, R. & Kidwell, D. (2014) Fundamentals of Corporate Finance, 3rd ed. London:
Wiley Publications
Petty, J.W., Titman, S., Keown, A., Martin, J.D., Martin, P., Burrow, M. & Nguyen, H. (2015).
Financial Management, Principles and Applications, 6th ed.. NSW: Pearson Education,
French Forest Australia
1 out of 5
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





