Course 27th September 2019: Correlation, Causation, and Analysis

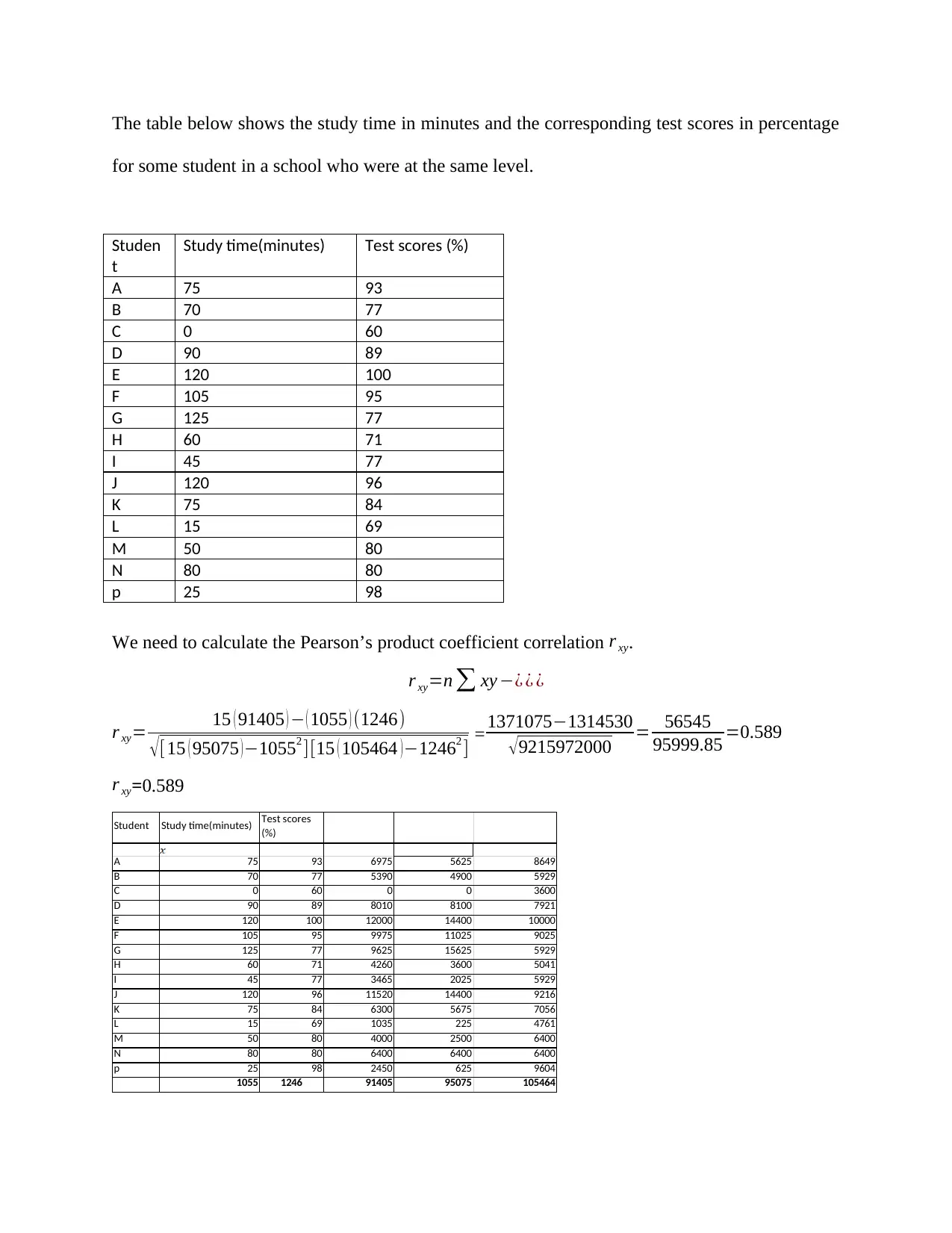
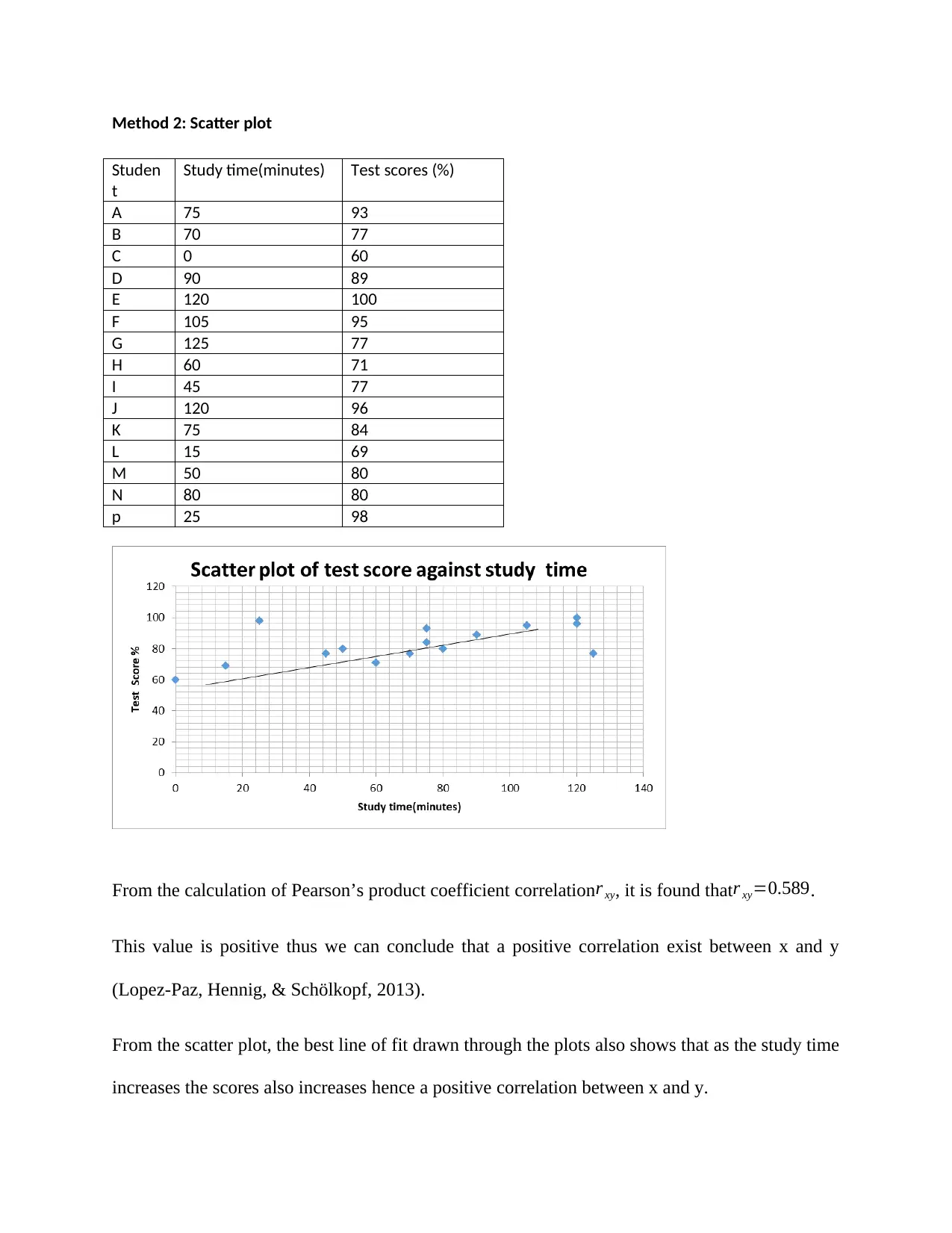
This assignment delves into the concept of correlation as a statistical measure of the linear relationship between two quantitative variables. It emphasizes that correlation does not automatically imply causation, and explores different scenarios where correlation may exist without a direct cause-and-effect relationship, such as reverse causation, common causal causes, and coincidental correlations. The assignment includes an illustrative example examining the correlation between study time and test scores, calculating the Pearson's product-moment correlation coefficient, and creating a scatter plot to visualize the relationship. Despite finding a positive correlation, the assignment clarifies that other factors like coincidence, differing student abilities, and motivation could influence test scores, not just study time. The assignment also discusses bidirectional causation where high test scores could motivate students to study more, and references several key statistical papers.

Mathematics Assignment
Student Name:
Instructor Name:
Course Number:
27th September 2019

Meaning of correlation
This term as used in statistics is simply defined as a measure of a linear relationship between
two quantitative variables.
Two variables x and y are said to have a correlation if a change in x results into a change
in y.
Correlation and causation
Existence of a correlation between x and y doesn’t automatically mean that one event causes the
other one (Mahdavi , 2013). In other words, correlation doesn’t imply causation.
This therefore calls for further investigation to determine whether there is actual cause-effect
relationship. This is because for two correlated events x and y, there are several possible
relationships that may exist (Székely & Rizzo, 2009). This may include
i) Reverse causation
This may mean that y causes x and no the other way round (Székely & Bakirov, 2017). For
example the faster the windmills rotate, the more the wind. Faster wind velocity doesn’t imply
that wind is caused by windmills.
ii) The common causal causes both x and y
iii)There is no connection between x and y i. e the correlation is by coincidence.
Is there correlation between study time (x) and the test scores?
Illustration

The table below shows the study time in minutes and the corresponding test scores in percentage
for some student in a school who were at the same level.
We need to calculate the Pearson’s product coefficient correlation r xy.
r xy=n ∑ xy −¿ ¿ ¿
r xy= 15 ( 91405 ) − ( 1055 ) (1246)
√[15 ( 95075 )−10552 ][15 ( 105464 )−12462 ] = 1371075−1314530
√9215972000 = 56545
95999.85 =0.589
r xy=0.589
Student Study time(minutes) Test scores
(%)
A 75 93 6975 5625 8649
B 70 77 5390 4900 5929
C 0 60 0 0 3600
D 90 89 8010 8100 7921
E 120 100 12000 14400 10000
F 105 95 9975 11025 9025
G 125 77 9625 15625 5929
H 60 71 4260 3600 5041
I 45 77 3465 2025 5929
J 120 96 11520 14400 9216
K 75 84 6300 5675 7056
L 15 69 1035 225 4761
M 50 80 4000 2500 6400
N 80 80 6400 6400 6400
p 25 98 2450 625 9604
1055 1246 91405 95075 105464
Studen
t
Study time(minutes) Test scores (%)
A 75 93
B 70 77
C 0 60
D 90 89
E 120 100
F 105 95
G 125 77
H 60 71
I 45 77
J 120 96
K 75 84
L 15 69
M 50 80
N 80 80
p 25 98

Method 2: Scatter plot
From the calculation of Pearson’s product coefficient correlationr xy, it is found that r xy=0.589.
This value is positive thus we can conclude that a positive correlation exist between x and y
(Lopez-Paz, Hennig, & Schölkopf, 2013).
From the scatter plot, the best line of fit drawn through the plots also shows that as the study time
increases the scores also increases hence a positive correlation between x and y.
Studen
t
Study time(minutes) Test scores (%)
A 75 93
B 70 77
C 0 60
D 90 89
E 120 100
F 105 95
G 125 77
H 60 71
I 45 77
J 120 96
K 75 84
L 15 69
M 50 80
N 80 80
p 25 98

However, despite there being a positive correlation between x and y we cannot conclude that
increase in study time causes an increase in test scores.
Increase in test score could have resulted from the following factors;
 Coincidence
The test scores could have increased as a result coincidence and not increase in time
hence there is no connection between study time and test scores.
 Different level of ability of the students.
The test scores obtained could have increased due to the students having different level of
ability and not due to increase in study time.
 Common cause
Motivation of the students could make the students to take more time while studying .At
the same time the students could be motivated to get score high marks in exams. Thus
motivation
could be the factor making the students to take more time reading and scoring highly
 Bidirectional causation
Perhaps taking more time studying results in an increase in test score. On the other hand
high test score could motivate the students to take more study time. Thus one may not say
with precision that increase in study time leads to an increase in test scores.

References
Lopez-Paz, D., Hennig, P., & Schölkopf, B. (2013). The Randomized Dependence Coefficient.
Conference on Neural Information Processing Systems, 5(2), 45-62.
Mahdavi , D. B. (2013). The Non-Misleading Value of Inferred Correlation: An Introduction to
the Cointelation Model. Wilmott Magazine, 67(5), 50–61.
Székely, G. J., & Bakirov, N. K. (2017). Measuring and testing independence by correlation of
distances. Annals of Statistics, 35(6), 2769–2794.
Székely, G. J., & Rizzo, M. L. (2009). Brownian distance covariance. Annals of Applied
Statistics, 3(4), 1233–1303.
(Lopez-Paz, Hennig, & Schölkopf, 2013)