Advanced Algorithm Analysis: CP5602 Solved Assignment and Insights

This document presents a comprehensive solution to an assignment on algorithm analysis, addressing key problems related to tree structures, search algorithms, sorting techniques, and recurrence relations. It includes a proof demonstrating the relationship between internal and external nodes in a tree where each internal node has three children, an O(lg2n) time algorithm for finding the kth smallest key in the union of two sorted arrays, an analysis of merge sort with insertion sort for small sublists, a solution using the master theorem for recurrence relations, and an algorithm for identifying a universal sink in an adjacency matrix. The solutions provide detailed explanations and complexity analyses, offering valuable insights for students studying advanced algorithm analysis. Desklib provides a platform to access this and many other solved assignments and past papers.

ALGORITHMS
By:
The Name of the class:
Professor:
The Name of The School:
The City and State where it is located:
The Date:

1.show if every internal node has exactly 3 children
When nI = 1, then nE = 2nI + 1 = 2+1=3.
When nI = 2, then nE = 2nI +1 = 4+1 = 5.
Let’s propose that the equation nE is correct for k’< k, that is, for any nI = k’< k, nE = 2nI +1.
Now let’s consider k= nI. Then, 2(k − 1) + 1 + (3 − 1) is equals to nE. The number of nodes
which are external is equal to the nodes which are external fora tree with k − 1 internal nodes
plus 3 (we added an internal node which must have 3 children) minus 1 (in creating the new
internal node, we made an external node into an internal node). Thus, nE = 2k − 2+ 3 = 2k + 1.
In a case where by three externals and 1 root => 3=2*1+1
Let’s Assume true n nodes in a given tree whereby: ne = 2ni + 1.
• A tree can have extended by addition of new nodes:
1. We are unable to add only 1 node without the violation of three--ary tree property
2.only two nodes cannot be added cannot be added without the violation of the three-ary for
Addition of 3 nodes all must be external.
• In such a case, one old external becomes internal, therefore we have: ni-new = ni +1
ne-new = ne-1+3 = 2ni +3
= (2ni +2) +1 = 2(ni +1) + 1
= 2ni-new+1
• Therefore ne-new = 2ni-new +1
-new in both sides cancels
Then Ne=2ni+1
2. an O(lg2n) time algorithm for defining kth smallest key.
The algorithm applies the divide-and-conquer technique to find the kth smallest key. In process
of divide-and-conquer, the sizes of arrays SS and TT which are both sorted will change. We
indicate the length of TT (or, SS) by len(T)len(T) (or len(S)len(S)).
Notations and Basic Idea:
median index of SS should be denoted by sm≜len(S)/2sm≜len(S)/2 and the median
of SS by S[sm]S[sm] At any iteration. Likewise, the median index of TT should be denoted
by tm≜len(T)/2tm≜len(T)/2 and the median of TT by T[tm]T[tm].
The basic idea says that we do the comparison of
sm+tmsm+tm with kk and S[sm]S[sm] with T[tm]
for the determination of which half part either right or right of which (T or S) array can be
discarded and the small sub-problem can be left to recursion.

The algorithm
1.case one (sm+tm≥ksm+tm≥k
Here we have to scenarios where by :
Case 1.1 S[sm]≥T[tm]S[sm]≥T[tm].
The right bigger half of array S can be discarded that is from S(sm) to its end. Recursively the k-th
Can be found by the left smaller half of S and the Smallest element of T.T and S are exchanged
case 1.1 symmetric.
The second scenario
Case 1.2
S[sm] is greater than S[sm]T[tm] and S[sm]T[tm] is greater than T[tm].
2. case 2 (sm+tm<ksm+tm<k):
The first scenario case 2.1 T[tm]≤. T[tm]S[sm]≤ S[sm]
Array’s left smaller half can be discarded. Recursively (k−tm)(k−tm)-th
The right larger half of S and the smallest element of S can be found.
The second scenario 2.2 T
[tm]>S[sm]T[tm]>S[sm].
Time complexity
Half of some array are discarded at each iteration. Therefore time complexity is O(lg(len(S))
+lg(len(T))), which is O(lgn) for the input arrays T and S of n in size
3.
a) sorting the sub lists
When inputting values of K in size, insertion sort in the worst –case time runs on Θ(k2). The
equation of the form (ak2+bk+c) usually gives the running time. the running time of the form
Therefore, time which is worst-case is essential in sorting of the sub lists which are in form of
n/k. each of k in length in the insertion sort:
T(k)=nk(ak2+bk+c)=ank+bn+cny

Where by y is an integer which is usually less than n. Therefore, to get bigger values of n, the
last two term of T(k) can be ignored. Hence T(k)=Θ(nk).
b) a merging the sublists.
we are having n elements; we divide into sub lists of k each of them into n/k sorted sublists in
length. We take two sub lists simultaneously carry on with combining them to enable us merge
the n/k sorted sublist into a single list of n in length which is sorted. This results into
log(n/k)log .And for each step n elements are been compared ,hence the entire procedure
whole runs at Θ(nlg(n/k)).
c)The biggest value in k
when a set of rules are modified for them to be having similar asymptotic time of running as the
one for ordinary com
Solution.
bination so, Θ(nlgn) must be similar to Θ(nk+nlg(n/k)) =Θ(nk+nlgn−nlgk)
in order to content this state, k should not grow asymptotically faster than lg n this is because
when k grow faster than lg n, the set of rules will speed at worst asymptotic time than Θ(nlgn)
because of the nk term. We need to consider for the state k=Θ(lgn), requirements cling to or do
not.
Let’s propose, k to be equal to Θ (lg n)
Θ(nk+nlg(n/k)) =Θ(nk+ n lgn−n lgk)
=Θ (n lg n +n lg n−n lg (lg n))
=Θ (2n lg n−n lg(lgn)) †
=Θ (n lg n)
†lg(lgn) is smaller compared to lg n for bigger quantities of n.
4.a) Recurrence
The recurrences of such form are applicable in master theorem
T(n)=At(n/b) +f(n)
In a case where a is greater or equals to one and b is greater than one they are continual and the
function f(n) is an asymptotically useful role. we have three scenarios:
case 1: A function f(n)= O (n log ba-e) for a particular continual E> 0, then T (n) = Θ (n log b a)
Scenario 2. A function f(n) = Θ (nlogb a logk n) having 1 k ≥ 0, then T (n) = Θ (nlogb a logk+1 n).

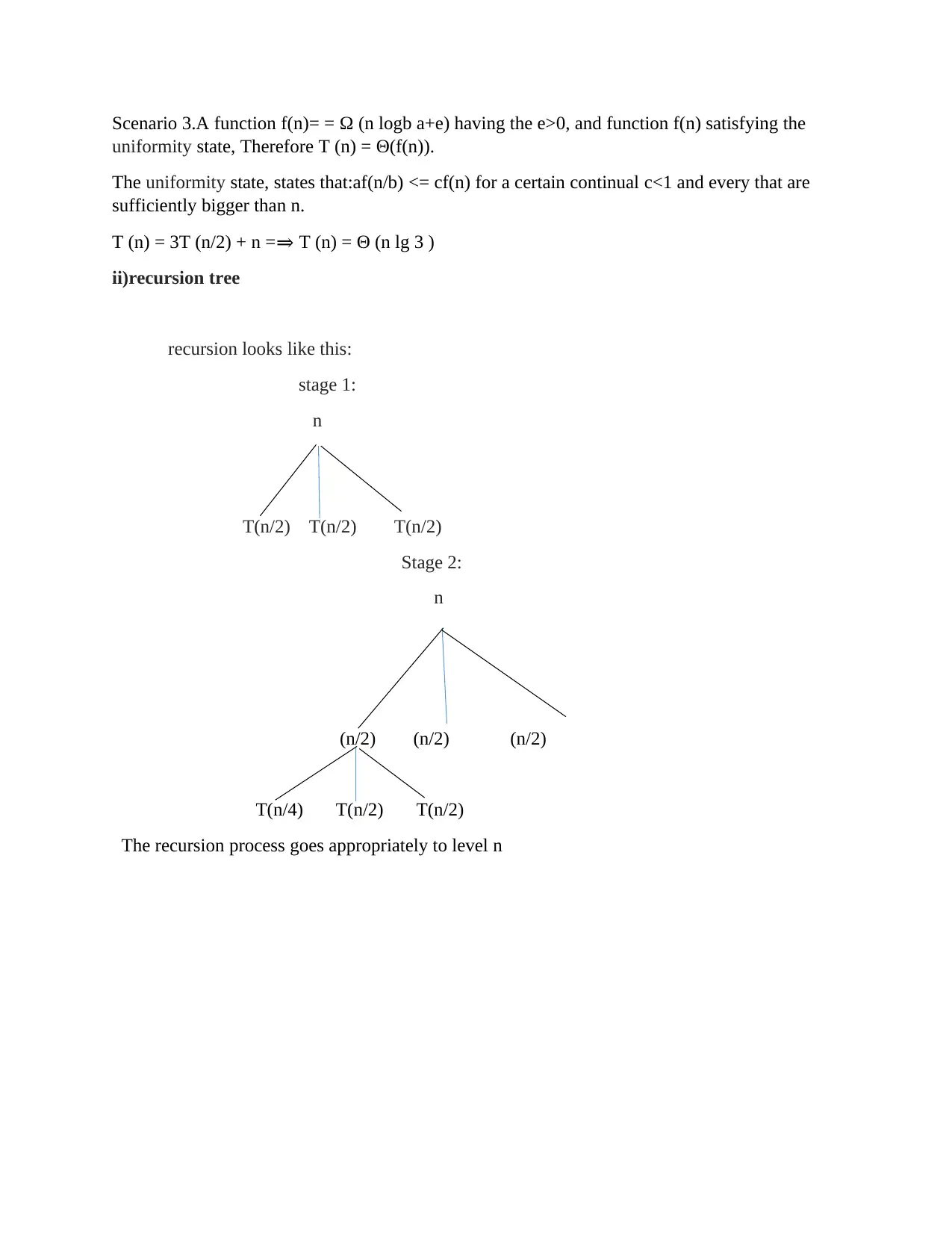
Scenario 3.A function f(n)= = Ω (n logb a+e) having the e>0, and function f(n) satisfying the
uniformity state, Therefore T (n) = Θ(f(n)).
The uniformity state, states that:af(n/b) <= cf(n) for a certain continual c<1 and every that are
sufficiently bigger than n.
T (n) = 3T (n/2) + n =⇒ T (n) = Θ (n lg 3 )
ii)recursion tree
recursion looks like this:
stage 1:
n
T(n/2) T(n/2) T(n/2)
Stage 2:
n
(n/2) (n/2) (n/2)
T(n/4) T(n/2) T(n/2)
The recursion process goes appropriately to level n

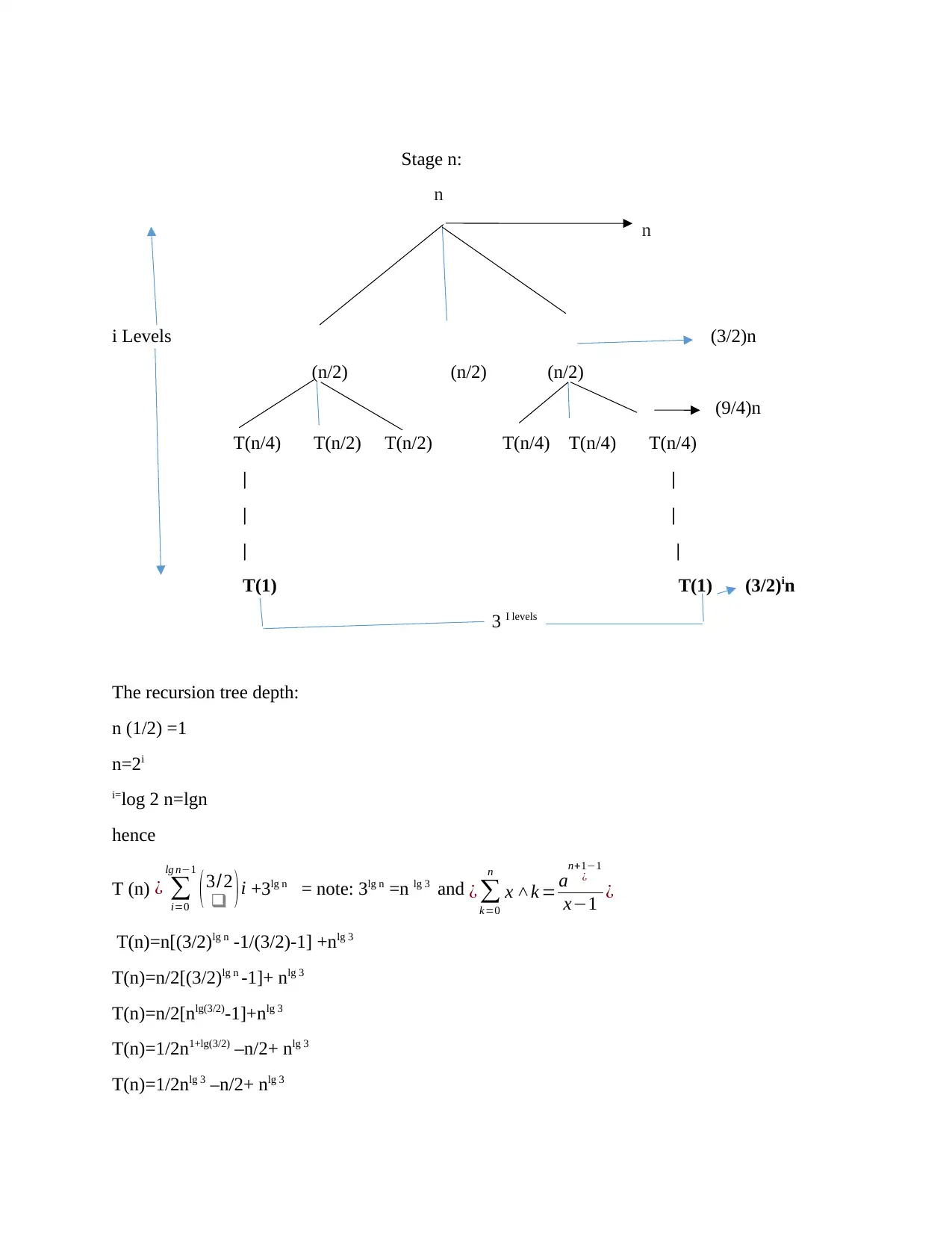
Stage n:
n
n
i Levels (3/2)n
(n/2) (n/2) (n/2)
(9/4)n
T(n/4) T(n/2) T(n/2) T(n/4) T(n/4) T(n/4)
| |
| |
| |
T(1) T(1) (3/2)in
3 I levels
The recursion tree depth:
n (1/2) =1
n=2i
i=log 2 n=lgn
hence
T (n) ¿ ∑
i=0
lg n−1
(3/2
❑ )i +3lg n = note: 3lg n =n lg 3 and ¿ ∑
k=0
n
x ˄k = an+1−1
¿
x−1 ¿
T(n)=n[(3/2)lg n -1/(3/2)-1] +nlg 3
T(n)=n/2[(3/2)lg n -1]+ nlg 3
T(n)=n/2[nlg(3/2)-1]+nlg 3
T(n)=1/2n1+lg(3/2) –n/2+ nlg 3
T(n)=1/2nlg 3 –n/2+ nlg 3

T(n)≤1/2 nlg 3 if -n/2+ nlg 3 ≥ 0
nlg 3-1≥≥1/2
T(n)=O(nlg 3)
We will choose C large so that:
T(1)=3T(└1/2┘+1=m 3T (0)+1=1≤(1) lg 3
T (2) =3T (└2/2┘) +2=3T (1) +2=5≤ c (2) lg 3
This holds for c ≥2
Substitution
T(n)=3T(└n/2┘) +n
T(n)≤3c (n/2) lg 3 +n
T(n)=3cnlg 3-2lg 3+n
T(n)=3cnlg 3+n
T(n)≤cn lg 3
5.Adjacency-matrix
According to the definition if a vertex I is a universal sink, the adjacency-matrix will be zero for
the ith row and one for the i-th column except in entry aii and a such vertex is only one. To be able
to find out if a universal sink really exist we then relate an algorithm for the same.
Starts from a11. we take one steep right if the current entry aij is equals to zero then j=j+1; if aij is
equal to 1 the for i=i+1 we take one step downwards. By doing these we will terminate at akn
ingress of the utmost cordon or akn of the last pier (n is equal to /V/,1 is equal to or less than k and
k is equal to or less than /v/). Starting by checking if the definition of universal sink is satisfied
by vertex k, if it is the we have found it, and if we cannot find it then there is no universal sink.
The total running time is given by O(V). Because we do consistently make a pace down or right,
then examining if an apex is a universal sink can be done in O(V).
No any vertex will be returned by this algorithm if there is no universal sink. The path that starts
from a11 will meet the u-th row or the u-th column at some entry if there is a universal sink u.
Once it’s on the track it cannot really get out of the track and will stop finally at the right entry.

References
Motwani, R., & Raghavan, P. (2010). Randomized algorithms(pp. 12-12). Chapman &
Hall/CRC.
Ali, K. H., Styczynski, Z. A., Shah, M. A., & Ramzan, M. (2014, December). Comparison
between two types of approaches matrix based and tree based to check connectivity between
nodes of a power system network. In Multi-Topic Conference (INMIC), 2014 IEEE 17th
International (pp. 494-499). IEEE.