Solution to Assignment 2: Advanced Algorithm Analysis - CP5602 Course
VerifiedAdded on 2023/03/30
|7
|826
|370
Homework Assignment
AI Summary
This document presents a detailed solution to an assignment on advanced algorithm analysis. It covers topics such as proving properties of trees with specific node structures, inserting data into heaps, binary search trees, AVL trees, and (2,4) trees. Additionally, it analyzes the time complexity of a modified merge sort algorithm using insertion sort for small sublists, determining the optimal value of k to maintain asymptotic running time. The solution also applies the master theorem and recursive tree method to solve recurrence relations and employs the brute force algorithm for pattern matching in a given text. Desklib offers a wide range of such solved assignments and past papers to aid students in their studies.

Running head: ANSWER TO ASSIGNMENT 2
ANSWER TO ASSIGNMENT 2
Name of the Student
Name of the University
Author Note
ANSWER TO ASSIGNMENT 2
Name of the Student
Name of the University
Author Note
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
1ANSWER TO ASSIGNMENT 2
1. In the question nI = internal nodes number, nE = number of external nodes.
To be proved: if every internal node in T has 3 children then nE=2nI +1
Let, this statement is true for lnodes (where l < n)
So, lE =2∗lI +1
Now, we increase the number of internal nodes by 1.
Hence, lInew = lI + 1.
Hence, lEnew = lE – 1+ 3 = 2∗lI +1 – 1 + 3 = (2mI + 2) + 1 = 2(lI + 1) + 1 = 2∗lInew +1
Thus in the same way it can be proved by method of induction when every internal
node of T has exactly 3 children then nE=2nI +1.
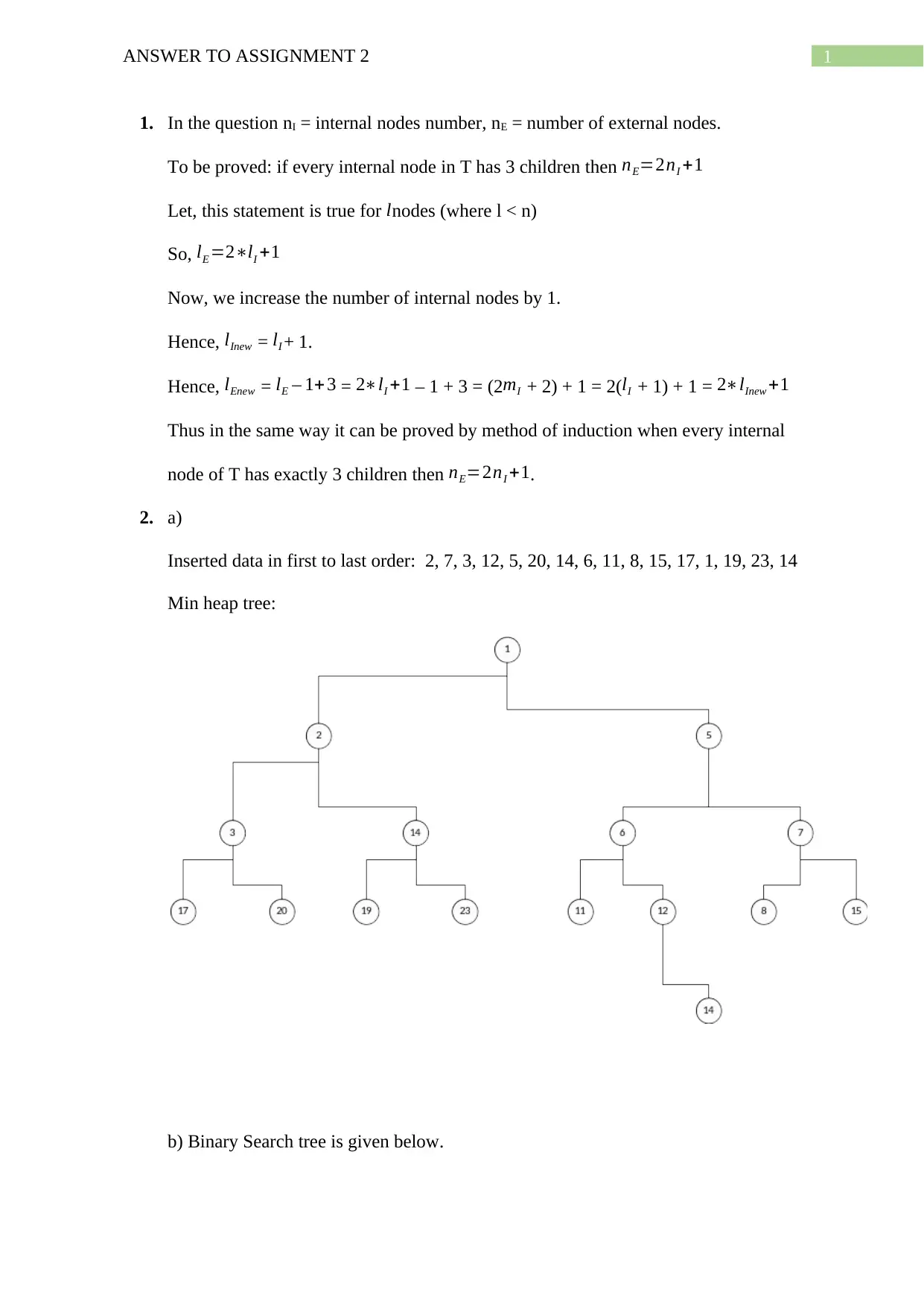
2. a)
Inserted data in first to last order: 2, 7, 3, 12, 5, 20, 14, 6, 11, 8, 15, 17, 1, 19, 23, 14
Min heap tree:
b) Binary Search tree is given below.
1. In the question nI = internal nodes number, nE = number of external nodes.
To be proved: if every internal node in T has 3 children then nE=2nI +1
Let, this statement is true for lnodes (where l < n)
So, lE =2∗lI +1
Now, we increase the number of internal nodes by 1.
Hence, lInew = lI + 1.
Hence, lEnew = lE – 1+ 3 = 2∗lI +1 – 1 + 3 = (2mI + 2) + 1 = 2(lI + 1) + 1 = 2∗lInew +1
Thus in the same way it can be proved by method of induction when every internal
node of T has exactly 3 children then nE=2nI +1.
2. a)
Inserted data in first to last order: 2, 7, 3, 12, 5, 20, 14, 6, 11, 8, 15, 17, 1, 19, 23, 14
Min heap tree:
b) Binary Search tree is given below.

2ANSWER TO ASSIGNMENT 2
c) AVL tree:
c) AVL tree:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3ANSWER TO ASSIGNMENT 2
d) [2,4] tree:
3.
i) Here, it is given that the input size is k and the worst case time complexity of
insertion sort is O(k^2). Thus the running time can be expressed in quadratic form
ak^2 + bk + c. Hence, the worst case time which is required to sort n/k sublists each
of length k size for insertion sort algorithm is provided by the following equation.
T(k) = (n/k)*(ak^2 + bk + c) = ank + bn + cn/k
For very large n the k become sufficiently small in comparison to n and thus the
second and third term of the above expression can be ignored.
Hence, T(k) = O(nk).
ii) Given, n elements are divided in n/k sorted sublists every one having length k.
Now, in order to merge the sorted sublists, 2 sublists are required to be taken at a time
and then merging is continued. Hence, the total steps required to merge n/k sorted
sublists is log(n/k). In each case n elements are compared and thus the time
complexity of the overall process will be O(nlog(n/k)).
iii) In a modified algorithm if the asymptotic running time is exactly same as the
standard time complexity of the standard sort then the time complexity O(nk +
nlog(n/k)) needs to be equal to O(nlogn).
Now, for satisfying the above condition increase of k can’t be faster than the
asymptotic increase of log(n) as if increase of k becomes faster than log(n) then
d) [2,4] tree:
3.
i) Here, it is given that the input size is k and the worst case time complexity of
insertion sort is O(k^2). Thus the running time can be expressed in quadratic form
ak^2 + bk + c. Hence, the worst case time which is required to sort n/k sublists each
of length k size for insertion sort algorithm is provided by the following equation.
T(k) = (n/k)*(ak^2 + bk + c) = ank + bn + cn/k
For very large n the k become sufficiently small in comparison to n and thus the
second and third term of the above expression can be ignored.
Hence, T(k) = O(nk).
ii) Given, n elements are divided in n/k sorted sublists every one having length k.
Now, in order to merge the sorted sublists, 2 sublists are required to be taken at a time
and then merging is continued. Hence, the total steps required to merge n/k sorted
sublists is log(n/k). In each case n elements are compared and thus the time
complexity of the overall process will be O(nlog(n/k)).
iii) In a modified algorithm if the asymptotic running time is exactly same as the
standard time complexity of the standard sort then the time complexity O(nk +
nlog(n/k)) needs to be equal to O(nlogn).
Now, for satisfying the above condition increase of k can’t be faster than the
asymptotic increase of log(n) as if increase of k becomes faster than log(n) then
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

4ANSWER TO ASSIGNMENT 2
because of having nk number of terms the algorithm time complexity will be poor
than worst case asymptotic time O(nlog(n)).
Now, if k = O(log(n)) then
O(nk + nlog(n/k)) = O(nk + nlog(n) – nlog(k)) = O(nlog(n) + nlog(n) – nlog(log(n)))
= O(2nlog(n) – nlog(log(n))) = O(nlog(n)) (as log(logn)) is significantly smaller than
log(n) for large n)
So, the best k value is O(log(n)).
4.
i) In general the master theorem is, if the recurrence relation is of form
T(n) = aT(n/b) + f(n)
Here,
a,b >=1 are positive constants and the function f(n) is asymptotically positive.
If f(n) = O (nlogb (a −e ) ) for some e > 0, then
T(n) = Θ ( nlogb a )
Now, the given recurrence relation is
T(n) = 3T(n/2) + n
a = 3, b = 2, e=1 and f(n) = n = nlog2 (3−1 )
Hence, T(n) = Θ ( nlog2 3 ) by Master theorem.
Hence, the tight asymptotic upper bound by Master theorem of the recurrence relation
is T(n) = Θ ( nlog2 3 ).
ii)
Recursive tree method:
because of having nk number of terms the algorithm time complexity will be poor
than worst case asymptotic time O(nlog(n)).
Now, if k = O(log(n)) then
O(nk + nlog(n/k)) = O(nk + nlog(n) – nlog(k)) = O(nlog(n) + nlog(n) – nlog(log(n)))
= O(2nlog(n) – nlog(log(n))) = O(nlog(n)) (as log(logn)) is significantly smaller than
log(n) for large n)
So, the best k value is O(log(n)).
4.
i) In general the master theorem is, if the recurrence relation is of form
T(n) = aT(n/b) + f(n)
Here,
a,b >=1 are positive constants and the function f(n) is asymptotically positive.
If f(n) = O (nlogb (a −e ) ) for some e > 0, then
T(n) = Θ ( nlogb a )
Now, the given recurrence relation is
T(n) = 3T(n/2) + n
a = 3, b = 2, e=1 and f(n) = n = nlog2 (3−1 )
Hence, T(n) = Θ ( nlog2 3 ) by Master theorem.
Hence, the tight asymptotic upper bound by Master theorem of the recurrence relation
is T(n) = Θ ( nlog2 3 ).
ii)
Recursive tree method:

5ANSWER TO ASSIGNMENT 2
At level 0 cost is n
Level 1 cost will be n/2 + n/2 + n/2 = 3n/2
Level 2 cost will be 9(n/4)
Let at x level the cost is 1.
Hence, by recursion T(n) = Θ ( nlog2 3 )
iii) In the similar way by substitution method it can be shown that for substitution
method the asymptotic bound is T(n) = Θ ( nlog2 3 )
Let, we guess the solution is Θ ( nlog2 3 ).
Now, it is needed to proved by mathematical induction that T(n) <= c*( nlog2 3)
Where, c is any positive constant.
T(n) = 3T(n/2) + n <= c(n/2)log(3)/log(2) + n <= c*n^(log(3)/log(2)) + n <= c*( nlog2 3).
5. Given text is ‘advancedalgorithmanalysis’. Now, for finding the ‘rithm’ pattern the
brute force algorithm is chosen to be employed.
Brute force algorithm:
Algorithm BruteForceMatch(T[0...n-1], P[0...m-1])
At level 0 cost is n
Level 1 cost will be n/2 + n/2 + n/2 = 3n/2
Level 2 cost will be 9(n/4)
Let at x level the cost is 1.
Hence, by recursion T(n) = Θ ( nlog2 3 )
iii) In the similar way by substitution method it can be shown that for substitution
method the asymptotic bound is T(n) = Θ ( nlog2 3 )
Let, we guess the solution is Θ ( nlog2 3 ).
Now, it is needed to proved by mathematical induction that T(n) <= c*( nlog2 3)
Where, c is any positive constant.
T(n) = 3T(n/2) + n <= c(n/2)log(3)/log(2) + n <= c*n^(log(3)/log(2)) + n <= c*( nlog2 3).
5. Given text is ‘advancedalgorithmanalysis’. Now, for finding the ‘rithm’ pattern the
brute force algorithm is chosen to be employed.
Brute force algorithm:
Algorithm BruteForceMatch(T[0...n-1], P[0...m-1])
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

6ANSWER TO ASSIGNMENT 2
for i ← 0 to n-m do
j ← 0
while j < m and P[j] = T[i+j] do
j++
if j = m then return i
return -1
for i ← 0 to n-m do
j ← 0
while j < m and P[j] = T[i+j] do
j++
if j = m then return i
return -1
1 out of 7
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




