ECM 561: Creative Lesson Plan for Junior Secondary Maths, Trigonometry

This assignment is a detailed lesson plan designed for teaching trigonometry to junior secondary mathematics students. The plan emphasizes creative teaching methods to enhance student understanding and engagement. The lesson plan incorporates a variety of activities, including evaluating triangles in polygons and exploring the concept of "What happens if...?" questions to encourage exploration and critical thinking. It also includes an activity where students design a clinometer to measure heights, promoting practical application of trigonometric principles. The plan addresses pre-requisite knowledge, real-life connections, and potential student challenges. The curriculum aims to foster mathematical creativity and talent development through exploration, pattern recognition, and hypothesis formulation. The lesson plan also includes reflections on teaching challenges and student engagement, incorporating strategies to make mathematics more enjoyable and interesting for students. The student will find this assignment on Desklib, a platform that provides past papers and solved assignments.

ECM 561 TEACHING THE CURRICULUM: JUNIOR SECONDARY MATHS
By Name
Course
Instructor
Institution
Location
Date

Introduction
Mathematics is a subject that attempts to comprehend patterns which permeate both the universe
around individuals as well as the mind. There are numerous ways of thinking; the type of
thinking one develops in mathematics is the ability to tackle abstraction besides solving
problems which need mathematics knowledge (Kullberg et al., 2017). Creativity has been
suggested as one of the main components to be incorporated in the education that is offered to
learners in the 21st century hence, the current curriculum ought to lay emphasis on the
development of the creative thinking of students. The main aim of mathematics education
revolves around mathematisation of the thinking of a learner. Clarity of thoughts as well as
pursing of the assumption to a conclusion that is logical and elaborate is pivotal to the
mathematical enterprise. Researchers have developed different dimensions of mathematics
creativity (Catarino et al., 2019).

Concept Map for Trigonometry
Description of Activities
Playfulness is treated as an integral bit in supporting creativity since numerous possible solutions
are explored in a spontaneous manner in play. This is termed as divergent thinking. Play revolves
around exploration as well as experimenting that can be done by a learner of any age (DhayantI
et al., 2018). When learners are experimenting and exploring, it is of essence that they have
choices: the choice to tackles a problem in various ways, the option of making mistakes or even
the choice of coming up with their own conjectures and determine their validity. In the first
activity, I will give the leaners the choice by asking them, ‘In how many ways can you…?’
question.

The aim of this activity is for the learner to become knowledge as well as gain confidence that
closed polygons may be divided into right angles. This will give allow them to do so when they
come across right angles triangles to use later in trigonometry problems for instance when
attempting to prove cosine rule. In such a way, being in a position to play with right-angled
triangles within a polygon may become a tool getting them unstuck in their later assignments
(Huang et al., 2019).
This task is ideal for learners that are exploring possibilities for themselves for the first time and
thereafter discussing the same with the other members of their class to gain more insights and
further refine their thinking.
Activities
Activity 1: Learners evaluating triangles in polygons
I will ask the learners:
 In how many ways can they divided each of the shapes shown below into triangle-angled
triangles?
Figure 1: Hexagon & equilateral triangle

Draw any shape of a right angled triangle. What closed polygon can you made by the triangle as
the main building block?
Figure 2: Right angle triangle
The figure below illustrates an example
Figure 3: A square from 8 right-angled triangles
 Is true that all closed polygons are made by right angled triangles? Explain your answer
Reflection on the teaching

I will reflect afterwards on what went as expected against that which failed after the activity.
Consideration is on questions which led the learners being interest as well as being able to move
on alongside those that needed to be clarified (Huang & Shimizu, 2016). The reflection will aid
in find a script that aids in engaging the learners to find mathematics not only enjoyable but also
interesting. They tend to be less likely involved in case they do not understand thing and are
unable to do something.
Use of the question “What happen if”
The first activity used the question ‘In how many ways…?’ to initiate the leaners to explore,
evaluate and play how a closed polygon might be made up of right angled triangles. Having the
option of how to get about this and making mistakes along the way, the learners were enthused to
take part in the assignment.
This activity will be seeking answers from the learners on ‘What happens if I change..?’ In
answering this question, the learner gets a feeling of ownership and a sense of valued for their
powers of thinking from generating their own conjectures and through the use of their own
examples to work on (Hanif et al., 2019). Collating information on the premise of such various
examples will as well enable generalization to be arrived at by the end of the activity.
The activity as well seeks to instruct the learners to first ponder about what would happen prior
to their ideas being tested. This should aid tem to take into consideration the thinking needed,
known as meta-cognition (Lin et al., 2018). They are likely to feel good when their thoughts turn
out to be right since they get it right. Should their conjectures turn out to be wrong, they may be
surprised and made to feel intrigued regarding ‘why is it that…?’

Activity 2: Leaners discover asking, ‘what happens if…?’
This activity demands the leaners to find out what would happen should they change the side or
even angle of a given triangle and to note the effect of such a change on the other angles or sides.
Part A
I will tell the student to do as below:
 Construct a right angle triangle and label it accordingly
Figure 4: Right-angled triangle example
In the table below, every row shows a transformation to an angle of side of the drawn triangle.
The empty cells should be completed with the manner in which the other sides or angles of the
triangle will change due to the transformation carried out.

 What do you realize?
 Why do you think it happens so?
Part B
In every row of the table below, you are provided with the size of angle C alongside the lengths
of the hypotenuse (side AB) and AC
Construct the triangles and find the values of the missing sides and angles
Still, generate a duplicate of the table and first note what you anticipate would occur prior to
confirming by drawing the rectangles

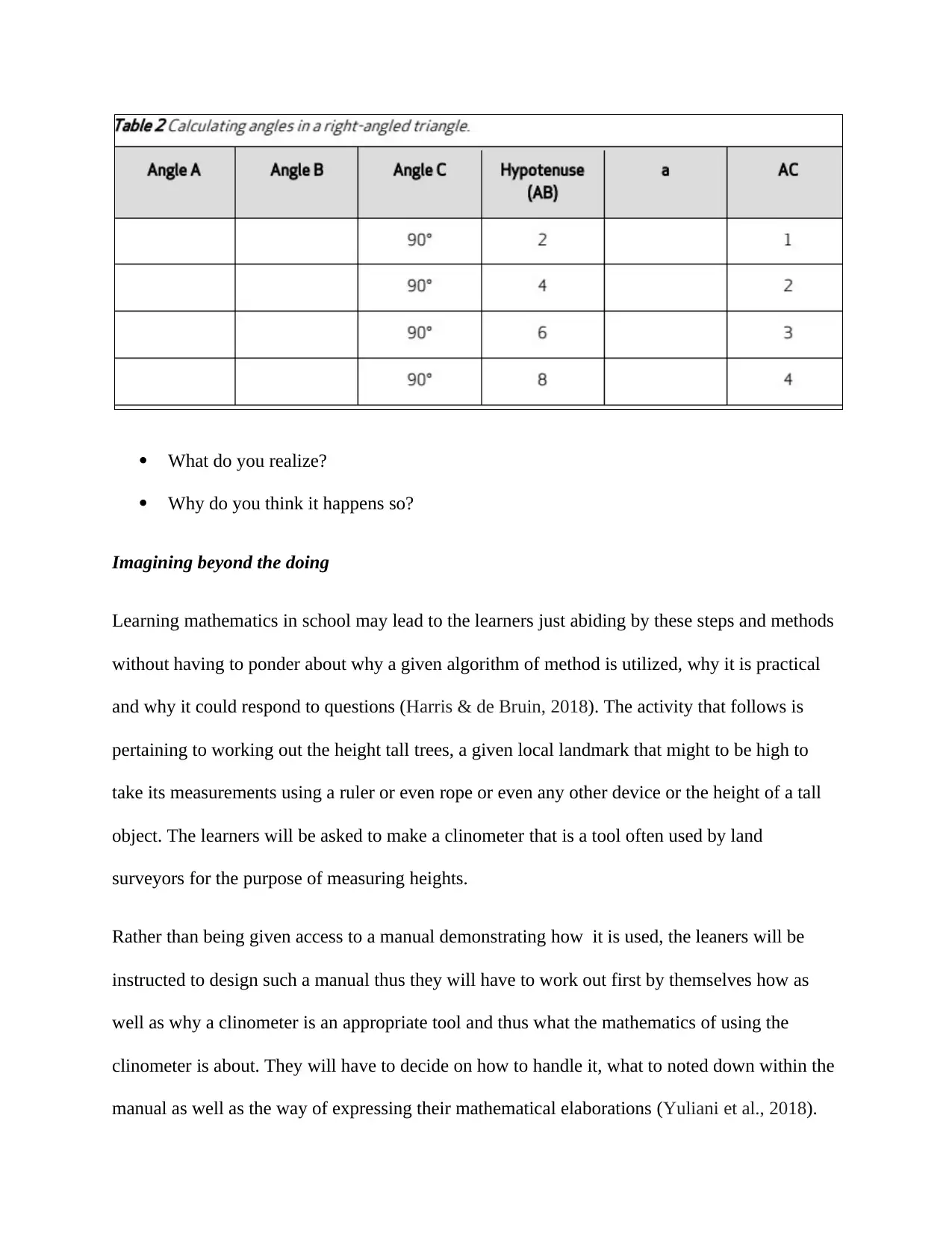
 What do you realize?
 Why do you think it happens so?
Imagining beyond the doing
Learning mathematics in school may lead to the learners just abiding by these steps and methods
without having to ponder about why a given algorithm of method is utilized, why it is practical
and why it could respond to questions (Harris & de Bruin, 2018). The activity that follows is
pertaining to working out the height tall trees, a given local landmark that might to be high to
take its measurements using a ruler or even rope or even any other device or the height of a tall
object. The learners will be asked to make a clinometer that is a tool often used by land
surveyors for the purpose of measuring heights.
Rather than being given access to a manual demonstrating how it is used, the leaners will be
instructed to design such a manual thus they will have to work out first by themselves how as
well as why a clinometer is an appropriate tool and thus what the mathematics of using the
clinometer is about. They will have to decide on how to handle it, what to noted down within the
manual as well as the way of expressing their mathematical elaborations (Yuliani et al., 2018).

Activity 3: Leaners coming up with a clinometer
The learners will be told as follows:
You are asked to come up with a clinometer in this activity. A clinometer is a device used by
surveyors in measuring the heights of tall buildings and structures alongside objects such as trees
and landmarks. You are thereafter asked to assume you work for a firm that design dn
manufactures such clinometer and you are tasked with coming up with the manual that bear the
instructions on its use (Lince, 2016). Bear in mind that your clients are land surveyors who are
extensively informed on mathematics and trigonometry therefore is at liberty to incorporate the
mathematical formulae as well as explanations on the way and reasons for a clinometer being
used in the estimation of heights. Making a clinometer would first call for modification of the
protractor as demonstrated in the figure below
Figure 5: Manufacture of clinometer
The clinometer works by taking measurements of the angle of elevation as demonstrated in the
figure below:

Figure 6: Illustration of elevation angle on clinometer
In the design of the manual, attempt answering the following questions that may be of help in
achieving the objectives of the manual:
 What are the various components of a clinometer? How does a clinometer work? What
mathematics is involved in a clinometer? The answers these questions may aid in
drawing what the leaners feels happens
 Determine how you may use a clinometer in working out the height of a tall object. What
is the mathematics behind the concept? The answers these questions may aid in drawing
what the leaners feels happens
 What is the scenario like when you stand at the base of a hill while the object that needs
to be measured is situated at the hilltop? Is a different method needed to measure the
height of the tall object or not?

 Come up with your manual to elaborate to the users the working of a clinometer and the
manner of using it. The use of drawings in the manual is integral in making it more
precise, clearer and more elaborate
Lesson Plan
Introduction
Mathematical creativity is an integral aspect in mathematical talent development. It is as well
important when it comes to construction of mathematical knowledge in a manner that is more
central than just generating leant knowledge hence teaching mathematics has to concentrate on
establishing solutions in a manner that is creative, exploration of pattern in a unique manner as
well as formulation of hypothesis (Jaworski et al., 2017). This following is a curriculum that can
be used in the creative teaching of junior secondary mathematics topic “Trigonometry” through
the exploration of various creativity techniques that would not only aid the learner to understand
the topic but also gain, to the greatest levels possible, the creativity in solving the mathematical
topic.
Description of Students
The class is made up of 40 learners, 12 girls and 28 boys. In a previous research on the attitude
of learners towards mathematics, 10 pupils answered in the negative. A readiness test illustrated
that 5 pupils could define the various sides of a right angled triangle. They could as well identify
the side that was 90 degrees and calculate a missing angle besides finding the area. It was at well
found that 2 pupils could use Pythagoras theorem to find the sides. More than half of the learners
could appreciate the values of learning Mathematics and gravitating positively towards its study.