Mathematics Major: RSA Cryptography and Prime Number Analysis

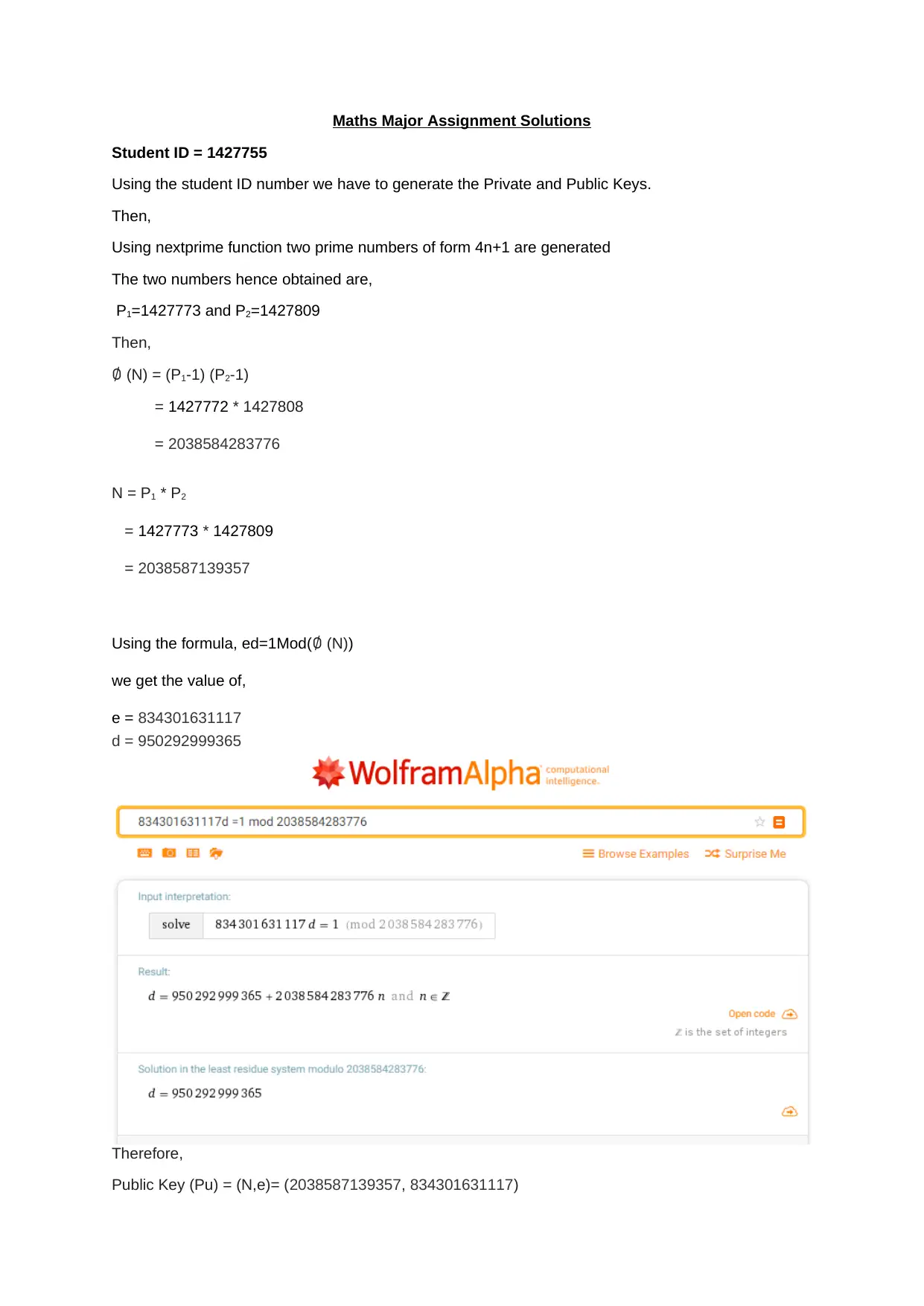
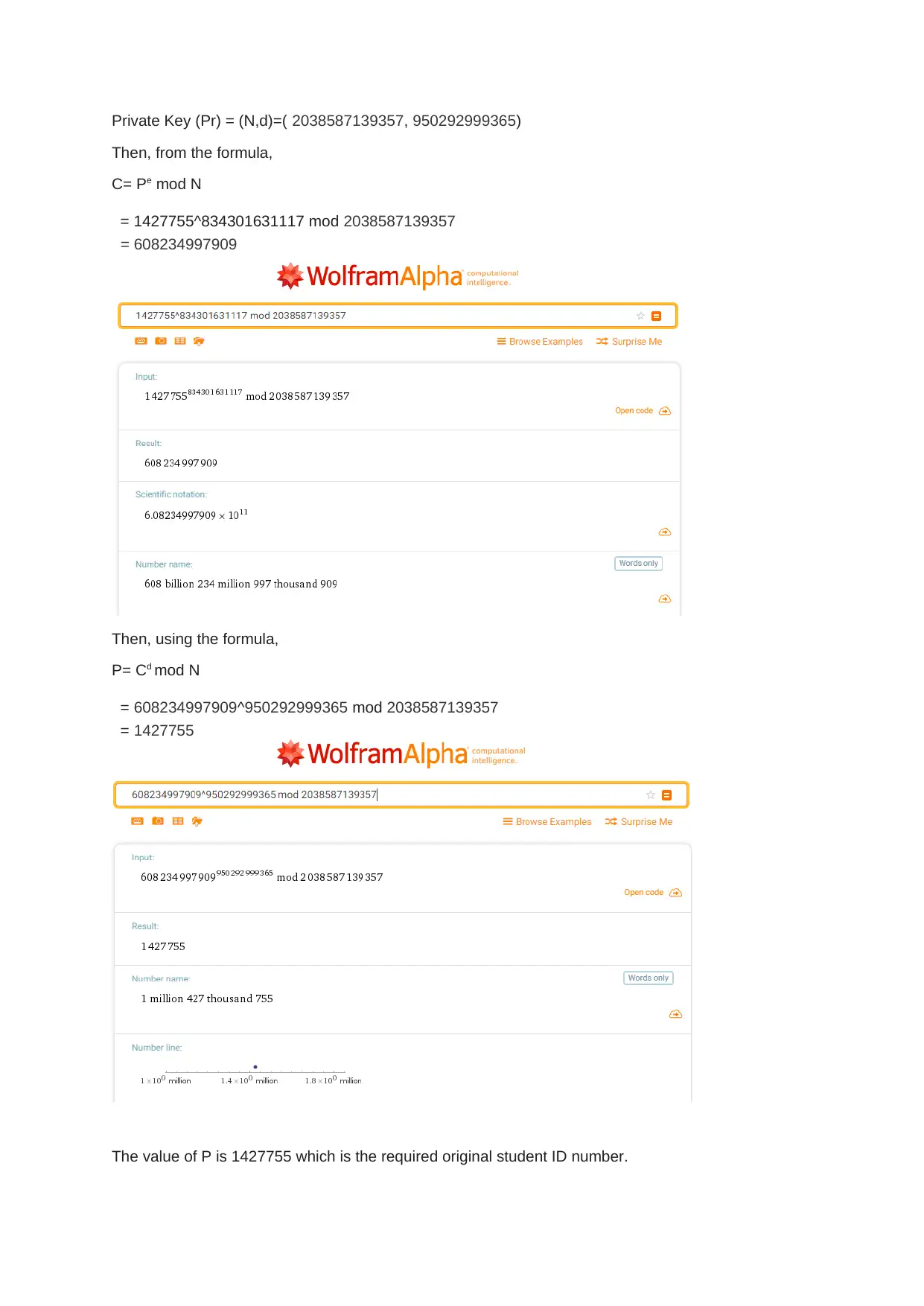
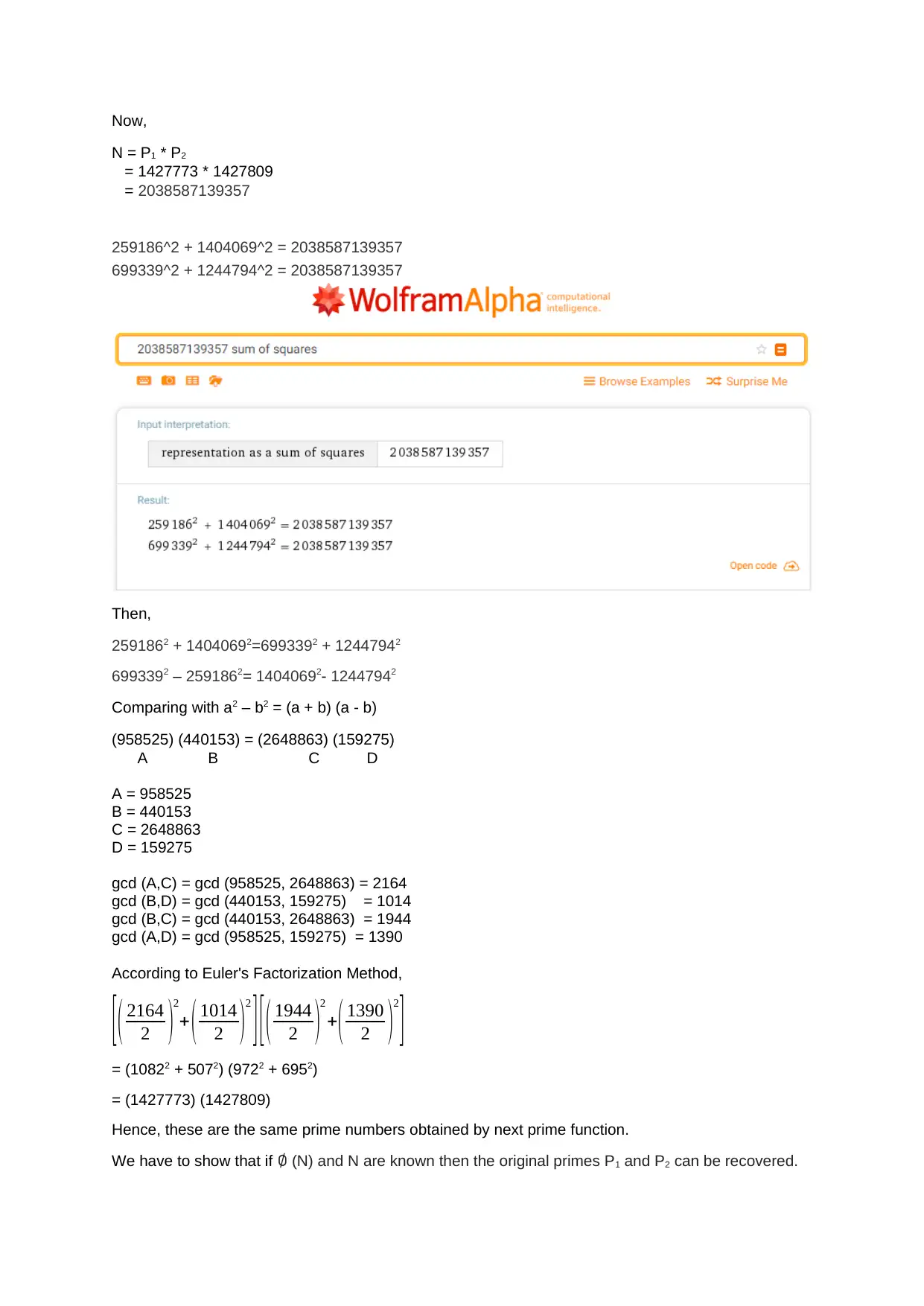
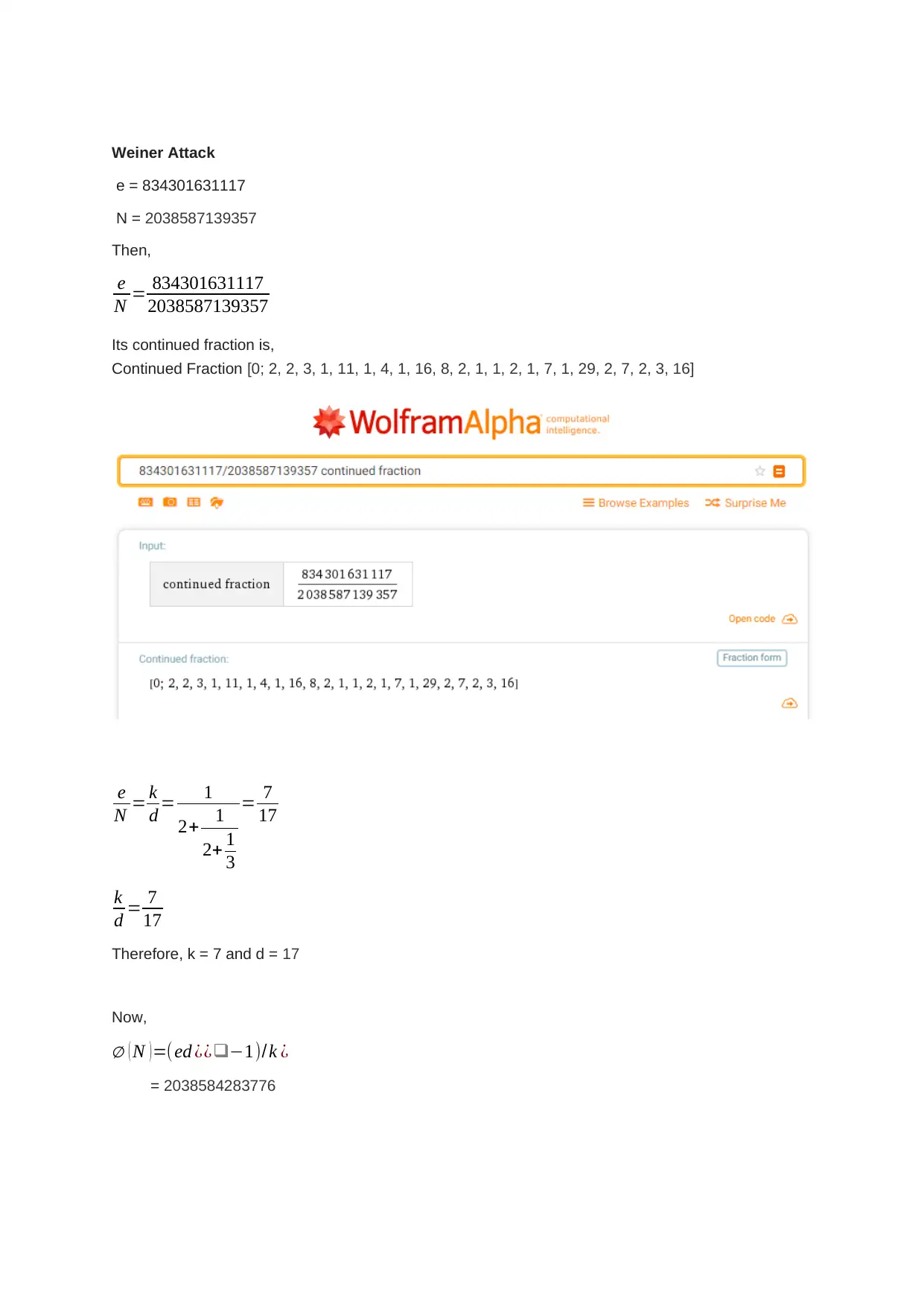
This assignment delves into the core concepts of RSA cryptography. It begins by generating public and private keys using a student ID and the nextprime function to find two prime numbers of the form 4n+1. The solution then demonstrates the encryption and decryption processes using modular exponentiation. Furthermore, the assignment explores breaking the keys by representing the prime numbers as the sum of two squares, drawing right-angled triangles, and applying Euler's Factorization Method. The solution also proves how the original primes P1 and P2 can be recovered if φ(N) and N are known. Finally, it investigates the Weiner attack, analyzing the continued fraction of e/N to potentially reveal the private key, and ultimately demonstrates how the prime factors can be recovered using the provided information, demonstrating the security considerations and vulnerabilities associated with RSA encryption.

Maths Major Assignment Solutions
Student ID = 1427755
Using the student ID number we have to generate the Private and Public Keys.
Then,
Using nextprime function two prime numbers of form 4n+1 are generated
The two numbers hence obtained are,
P1=1427773 and P2=1427809
Then,
∅ (N) = (P1-1) (P2-1)
= 1427772 * 1427808
= 2038584283776
N = P1 * P2
= 1427773 * 1427809
= 2038587139357
Using the formula, ed=1Mod(∅ (N))
we get the value of,
e = 834301631117
d = 950292999365
Therefore,
Public Key (Pu) = (N,e)= (2038587139357, 834301631117)

Private Key (Pr) = (N,d)=( 2038587139357, 950292999365)
Then, from the formula,
C= Pe mod N
= 1427755^834301631117 mod 2038587139357
= 608234997909
Then, using the formula,
P= Cd mod N
= 608234997909^950292999365 mod 2038587139357
= 1427755
The value of P is 1427755 which is the required original student ID number.

Breaking the keys:
P1= 1427773
P2= 1427809
The numbers P1 and P2 are then represented as the sum of two squares.
(1082)2 + (507)2 = 1427773
(695)2 + (972)2 = 1427809
Then, two right angled triangles are drawn,
So, For the 1st triangle
C = n2 + (2m + n - 1)2
= 5072 + (2m + 507 - 1)2
(1082)2 = (2m + 507 - 1)2
2m = 1082–506
m = 288
So, (m1, n1) = (288, 507)
For 2nd triangle,
C = n2 + (2m + n - 1)2
= 6952 + (2m + 695 - 1)2
(972)2 = (2m + 695 - 1)2
2m = 972 – 694
m = 139
So, (m2, n2) = (139, 695)
√1427773
507
1082
√1427809
695
972

Now, Let P1 = C1 and P2 = C2 and let the smallest value of the two squares be n
For the 1st triangle,
a = (2m - 1)(2m + 2n - 1)
= (576 -1) (576 + 1014 - 1)
= 913675
b = 2n (n + 2n -1)
= 1014 (507+ 1014 -1)
= 1541280
C = n2 + (2m + n - 1)2
= 257049 + (576 + 507 - 1)2
= 1427773
For the 2nd triangle,
a = (2m - 1)(2m + 2n - 1)
= (278 - 1)(278 +1390 -1)
= 461759
b = 2n (n + 2n -1)
= 1390 (695 + 1390 -1)
= 2896760
C = n2 + (2m + n - 1)2
= 483025 + (278+695-1)2
=483025 +944784
= 1427809
c1
a1
b1
c2
a2
b2

Now,
N = P1 * P2
= 1427773 * 1427809
= 2038587139357
259186^2 + 1404069^2 = 2038587139357
699339^2 + 1244794^2 = 2038587139357
Then,
2591862 + 14040692=6993392 + 12447942
6993392 – 2591862= 14040692- 12447942
Comparing with a2 – b2 = (a + b) (a - b)
(958525) (440153) = (2648863) (159275)
A B C D
A = 958525
B = 440153
C = 2648863
D = 159275
gcd (A,C) = gcd (958525, 2648863) = 2164
gcd (B,D) = gcd (440153, 159275) = 1014
gcd (B,C) = gcd (440153, 2648863) = 1944
gcd (A,D) = gcd (958525, 159275) = 1390
According to Euler's Factorization Method,
[ ( 2164
2 )
2
+ ( 1014
2 )
2
][ ( 1944
2 )
2
+( 1390
2 )
2
]
= (10822 + 5072) (9722 + 6952)
= (1427773) (1427809)
Hence, these are the same prime numbers obtained by next prime function.
We have to show that if ∅ (N) and N are known then the original primes P1 and P2 can be recovered.

N = P1 * P2
= 1427773* 1427809
= 2038587139357
∅ (N) = (P1-1) (P2-1)
= (1427773- 1) (1427809 - 1)
= 2038584283776
We have,
∅ (N) = (P1-1) (P2-1)
∅ (N) = P1P2 – P1 – P2 + 1
∅ (N) = N – P1 – P2 + 1
P1 + P2 = N - ∅ (N) +1
Then,
P2 = N - ∅ (N) +1 – P1
P1 = N - ∅ (N) +1 – P2
So,
N = P1 (N - ∅ (N) +1 – P1)
= P1N – P1∅ (N) + P1- P12
0 = P12 + P1 (∅ (N) – N - 1) + N
Comparing with the equation ax2 + bx + c = 0, x=−b ± √ b2−4 ac
2 a
a = 1
b = ∅ (N) – N – 1
= -2855582
c = 2038587139357
Then, putting the values of a, b and c in the equation,
For negative sign, x = 1427773 = P1
For positive sign, x = 1427809 = P2

Weiner Attack
e = 834301631117
N = 2038587139357
Then,
e
N = 834301631117
2038587139357
Its continued fraction is,
Continued Fraction [0; 2, 2, 3, 1, 11, 1, 4, 1, 16, 8, 2, 1, 1, 2, 1, 7, 1, 29, 2, 7, 2, 3, 16]
e
N = k
d = 1
2+ 1
2+ 1
3
= 7
17
k
d = 7
17
Therefore, k = 7 and d = 17
Now,
∅ ( N ) =(ed ¿¿❑−1)/k ¿
= 2038584283776

We have,
∅ (N) = (P1-1) (P2-1)
∅ (N) = P1P2 – P1 – P2 + 1
∅ (N) = N – P1 – P2 + 1
P1 + P2 = N - ∅ (N) +1
Then,
P2 = N - ∅ (N) +1 – P1
P1 = N - ∅ (N) +1 – P2
So,
N = P1 (N - ∅ (N) +1 – P1)
= P1N – P1∅ (N) + P1- P12
0 = P12 + P1 (∅ (N) – N - 1) + N
Comparing with the equation ax2 + bx + c = 0, x=−b ± √ b2−4 ac
2 a
a = 1
b = ∅ (N) – N – 1
= -2855582
c = 2038587139357
Then, putting the values of a, b and c in the equation,
For negative sign, x = 1427773 = P1
For positive sign, x = 1427809 = P2