Final Exam: CSC 3110 Problem Solving and Programming, Winter 2020

This document presents a comprehensive solution to the CSC 3110 final exam, focusing on problem-solving and programming concepts. The exam covers a range of topics, including algorithm analysis, with specific questions on Big O notation, and function equivalence. It also delves into algorithm design techniques, such as dynamic programming, and iterative improvement, with detailed explanations and examples. The solution provides step-by-step answers to questions on algorithm efficiency, and shortest path problems using Dijkstra's algorithm. Furthermore, the solution explains the main idea of dynamic programming and its comparison with divide-and-conquer, as well as the concept of prefix-free codes in Huffman coding. Finally, the document illustrates the application of the shortest-augmenting path algorithm to determine maximum flow and minimum cut in a network, making it a valuable resource for students seeking to understand and excel in their computer science studies.

CSC 3110
Problem Solving and Programming
Section 901
Winter Term 2020
Final Exam
Name:____________________________________________________
Please read the following comments before beginning the exam.
The final exam consists of five questions and the allowed time is sixty minutes. The questions
may be worth differing numbers of points, so consider this when answering the questions. The
points for each question are shown below. The exam is worth a total of 265 points. The exam is
closed book /closed notes – NOT the case at this point. To receive full credit, all your answers
must be justified.
Must turn in 1 single document containing all answers, hand writing must be clear/readable/clean!
Question 1 (80 Points) __________________
Question 2 (40 Points) __________________
Question 3 (35 Points) __________________
Question 4 (55 Points) __________________
Question 5 (55 Points) __________________
Total (265 Points) __________________

Question 1 (80 points):
Part a (20 points):
Solution
Only assertion b) is true
n(n+1)/2 = n2/2 + n/2 = O(n2)
O(N^2) would mean (roughly) that the number of steps to calculate it grows like N^2, for large
N
Part b (20 points):
Solution
a. Consider the function –
.
The function is equivalent to .

Formally, it is proved by applying the limit.
Therefore, .
b. Consider the function –
.
Therefore, .
Part c (40 points):
Consider the following algorithm.

a. What does this algorithm compute?
b. What is its basic operation?
c. How many times is the basic operation executed?
d. What is the efficiency class of this algorithm?
e. Suggest an improvement, or a better algorithm altogether, and indicate its efficiency
Solution
a. This algorithm computes difference between array’s largest element and smallest
element.
b. The algorithm’s basic operation is element comparison.
c. Let us denote C(n) the number of times the basic operation (element comparison) is
executed and expressing it as a function of size n.The algorithm makes two comparisons
on each execution of the loop, which is repeated for each value of the loop’s variable i
within the bounds 1 and n-1.Therefore,
This is an easy sum to compute because it is nothing else but 1 repeated n-1 times. Thus,

d. The efficiency class of this algorithm is
e. The given algorithm contains two if statements to compare the elements. But the
algorithm does not require making these two comparisons always.
• For example, if the element is less than minval, then it never greater than maxval.
• Thus, the second comparison (A[i]>maxval) can be ignored, when A[i] <minval is true.
• The given algorithm can be improved by replacing the two if statements by one if-else
construct as follows:
The efficiency class is as follows:
The efficiency class of the improved algorithm is same as the efficiency class of the
given algorithm. However, the improved algorithm is somewhat better than the given
algorithm.
Question 2 (40 points)
Part a (25 points):
Consider the problem of finding the smallest and largest elements in an array of n numbers.
Design a presorting-based algorithm for solving this problem and determine its efficiency class.

Solution
Part b (15 points):

Compare the efficiency of the three algorithms: (i) the brute-force algorithm, (ii) this presorting-
based algorithm, and (iii) the divide-and conquer algorithm.
Solution
For searching the largest and the smallest in the given array in the brute force and divide and
conquer algorithms we scan the entire array one time only, so that’s the efficiency of this
algorithm is linear, whereas this presorting based is of nlogn class. So, they said search
algorithms are superior to the presorting based algorithm
Question 3 (35 points):
Part a (15 points):
What is the main idea of Dynamic Programming Algorithm design technique?
Solution
The main idea of dynamic programming algorithm design technique we break the problem into
sub problems and solve them, after that we combine the results of all the sub problems to get the
final result. It is a type of recursion, where we break the code into sub parts until we reach the
base condition, but the difference is, here we store the result of sub problem into a table, so that
we do not have to compute the sub problem again, we can simply use the stored result. it reduces
the time complexity from exponential time to polynomial time.
Part b (20 points):
What does dynamic programming has in common with divide-and-conquer? What is a principal
difference between them?
Solution
 Both energetic software design and division and defeat deal with subproblems. i.e. both
deal with slighter problems of the similar question
 The principal difference is that self-motivated programming expressions for best solution
to a subproblem, whereas DnC could not.

Question 4 (55 points):
Part a (15 points):
What are the two types of codes discussed in the class and what is Prefix-free code?
Solution
If prefix free codes aren’t used in Huffman coding, then it will cause problems in both encoding
and decoding.
Huffman Codes are known as prefix free codes - which means in Huffman coding no code word
can be prefix of any other code word. Suppose, in Huffman coding the code word for "e" is 10
for a specific example. That means no other code word can begin with 10. So, if prefix free
codes aren’t used in Huffman coding then it will cause a problem in encoding and will create
confusion.
Prefix free codes allows the decoding process to follow a greedy approach. In this case the user
read the encoded string from left to right and when a code word is seen, a character can be
outputted. Let us assume the code for character 'E' is 0000. Now, 0, 00 and 000 does not do not
code anything and the user keeps bit reading. When the code is '0000' it encodes "E" as there
cannot be any other code word of the form 0000x as it is prefix free. So, the user can output "E'
and starts again. Similarly, if there is a 1, then it encodes nothing but '10' encodes 'e'. So, the user
can output 'e' as no other code word can begin with 10 and so on. So, if prefix free codes aren’t
used in Huffman coding then it will cause a problem in decoding and will cause problems.
Part b (40 points):
Solve the following instances of the single-source shortest-paths problem with vertex ‘a’ as the
source. Show vertices labels at each iteration and the shortest paths and their lengths.

Solution
Consider the graph below,
Apply the single-source shortest-paths procedure with vertex a as the source. The following is
the table that contains each step and its illustration. The next closest vertex is shown in bold.

The shortest paths are:
from a to d: a – d of length 7
from a to b: a – d – b of length 9
from a to c: a – d – c of length 12
from a to e: a – d – b – c – e of length 18
Question 5 (55 points):
Part a (20 points):

Explain how Iterative Improvement Algorithm design technique solves optimization
problems? Name two obstacles to the successful implementation of this technique.
Solution
The iterative improvement technique involves finding solutions for an optimization problem by
generating a series of executable solutions that improve the value of the target function of the
problem.
 Each subsequent solution in such a sequence typically involves a small local change in
the previous executable solution.
 If such changes do not improve the value of the target function, the algorithm returns the
last possible solution as optimal and stops.
Important problems that can be solved with the iterative improvement algorithm are linear
planning, maximizing the flow in the network, and matching the maximum number of vertices in
the graph.
 A simple method is a classic way to solve common linear programming problems.
 Works by generating a sequence of adjacent extreme points in the problem executable
area while improving the value of the target function.
The two obstacles are:
1. First, you need the first executable solution.
2. Next, it is not always clear which changes you need to allow in the solution you can
implement to ensure that the current solution is locally optimal and otherwise replace it with a
better solution.
Part b (35 points):
Apply the shortest-augmenting path algorithm to find a maximum flow and a minimum cut in the
following networks: (show all labels)

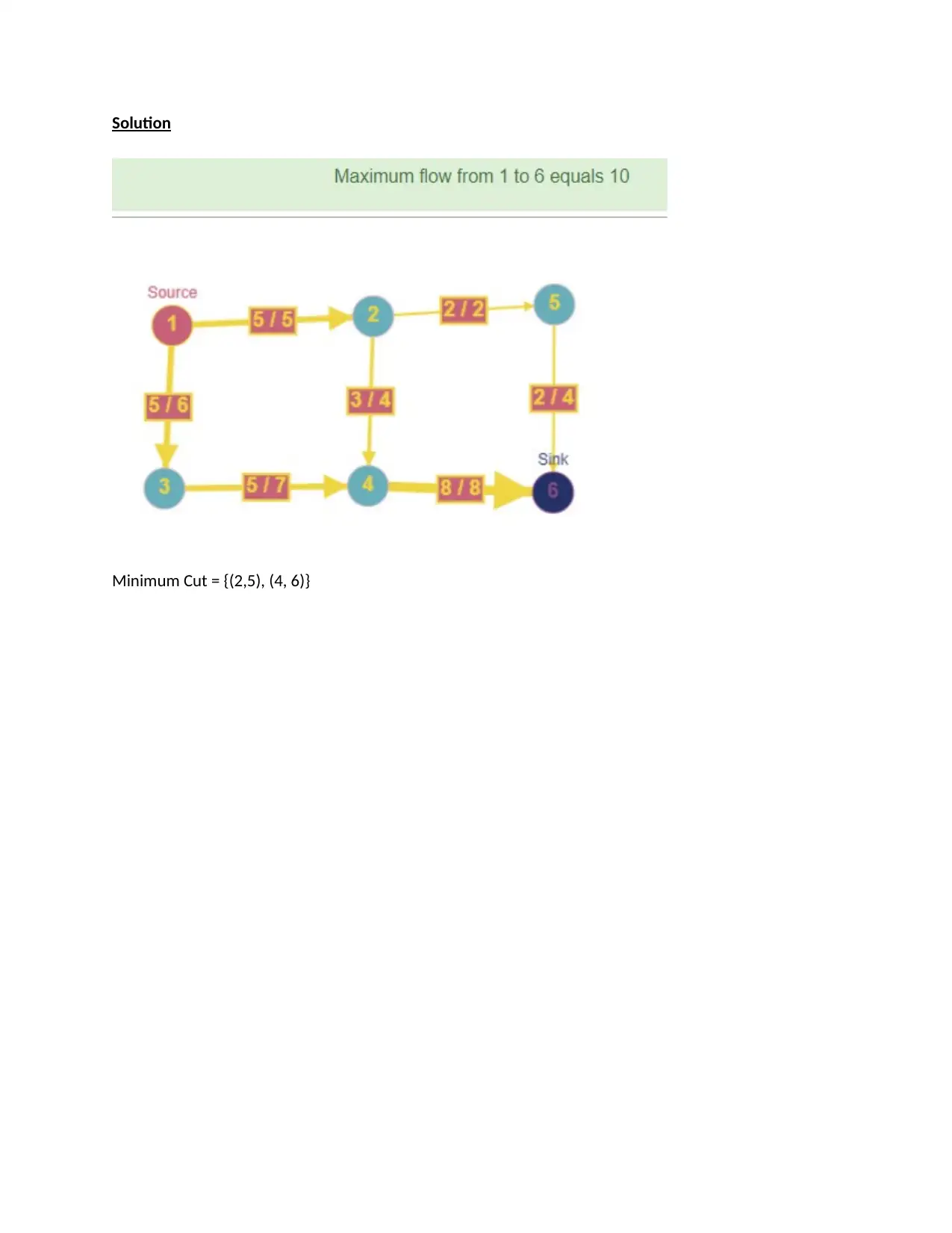
Solution
Minimum Cut = {(2,5), (4, 6)}