Comprehensive Data Analysis Report for Finance and Economics

This report provides a comprehensive analysis of statistical data in finance and economics, employing various techniques to derive meaningful insights. It addresses questions related to correlation, normal distribution, probability, central tendency, quartiles, dispersion, regression analysis, and hypothesis testing. The analysis includes scatter diagrams, calculations of correlation coefficients, construction of normal distribution curves, and Z-tests. Specific calculations and interpretations are provided for each question, covering topics such as probability of selecting students based on gender and age, determination of mode, median, mean, quartiles, range, mean deviation, variance, and standard deviation. The report also includes a regression analysis, examining the relationship between variables and commenting on the fit of the regression line. Furthermore, it interprets estimations in a regression equation involving multiple variables. The conclusion summarizes the findings and their implications within the context of finance and economics. Desklib provides access to similar solved assignments and past papers for students.

Data analysis for
finance and economics

Contents
Contents...................................................................................................................................................2
INTRODUCTION...................................................................................................................................3
QUESTION 1...........................................................................................................................................3
a. Draw a scatter diagram to represent the data.............................................................................3
b. From (a) is the relationship roughly linear? What is the direction?..........................................4
a. Calculate the value of the correlation coefficient r....................................................................4
QUESTION 2...........................................................................................................................................5
QUESTION 3...........................................................................................................................................6
QUESTION 4...........................................................................................................................................8
QUESTION 5.........................................................................................................................................10
(b) Calculation of the regression equations:......................................................................................10
3. Least square regression coefficients..............................................................................................10
(c) squared correlation coefficient.....................................................................................................11
d) comment on the regression line.....................................................................................................12
QUESTION 6.........................................................................................................................................12
QUESTION 7.........................................................................................................................................13
QUESTION 8.........................................................................................................................................13
CONCLUSION......................................................................................................................................17
References................................................................................................................................................1

INTRODUCTION
Data can be defined as a set of figures or information that is used to generate information
about the topic. By analyzing this data, an analyst can draw a lot of information that can be used for
taking decision. It helps companies in managing the operations if the company and bringing out
effective results out of it (Ravid, 2019). The report is based on the calculation and analysis of
statistical data with the help of various techniques. There are seven questions under this report. The
first one deals in correlation. The second one prepares a normal distribution and its graph. The third
query is about the probability and forth question prepares central tendency, quartiles and dispersion.
The fifth one calculates the correlation coefficient and regression analysis. The sixth question
conducts the Z – test for the hypothesis. The seventh sections construct a tree diagram and the eighth
one interprets the estimations in regression equation.
QUESTION 1
a. Draw a scatter diagram to represent the data.
Participant A B C D E F H
Number of bottle (1 litre) of
water [X] 2 4 3 2 5 1 3
Number of hours staying
awake [Y] 5 7 5 4 7 4 6

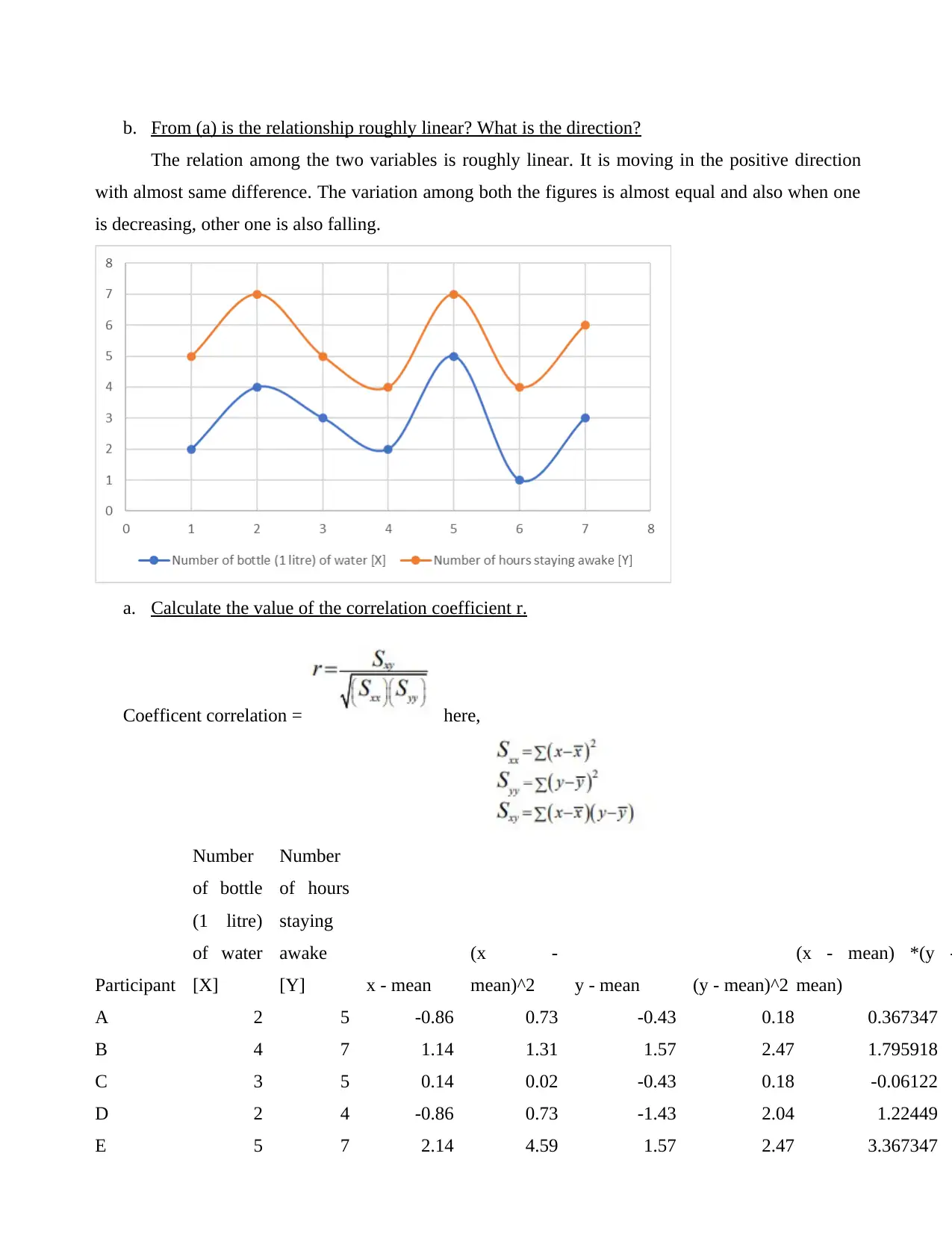
b. From (a) is the relationship roughly linear? What is the direction?
The relation among the two variables is roughly linear. It is moving in the positive direction
with almost same difference. The variation among both the figures is almost equal and also when one
is decreasing, other one is also falling.
a. Calculate the value of the correlation coefficient r.
Coefficent correlation = here,
Participant
Number
of bottle
(1 litre)
of water
[X]
Number
of hours
staying
awake
[Y] x - mean
(x -
mean)^2 y - mean (y - mean)^2
(x - mean) *(y -
mean)
A 2 5 -0.86 0.73 -0.43 0.18 0.367347
B 4 7 1.14 1.31 1.57 2.47 1.795918
C 3 5 0.14 0.02 -0.43 0.18 -0.06122
D 2 4 -0.86 0.73 -1.43 2.04 1.22449
E 5 7 2.14 4.59 1.57 2.47 3.367347

F 1 4 -1.86 3.45 -1.43 2.04 2.653061
H 3 6 0.14 0.02 0.57 0.33 0.081633
Mean 2.857143 5.428571 10.86 9.71 9.428571
r = 9.428571 / √ (10.86) * (9.71)
= 9.428571 / 10.26
= 0.918
c. Do we have a weak, strong, perfect or imply no correlation between the two variables? Justify
your answer
The Correlation among the two variables is very strong as the value received is near about 1
which is 0.91. This shows a nearly perfect relationship among them.
QUESTION 2
a. What percentage (to 3 decimal places) of the students scored more than 80?
According to the formula applied in excel, the figure comes out to be 92.56 %.
b. What percentage (to 3 decimal places) of the students scored under 65?
Here the number of students who are under the score of 65 is expected to be 4.32 %.
c. What percentage (to 3 decimal places) of the students scored between 67 and 90?

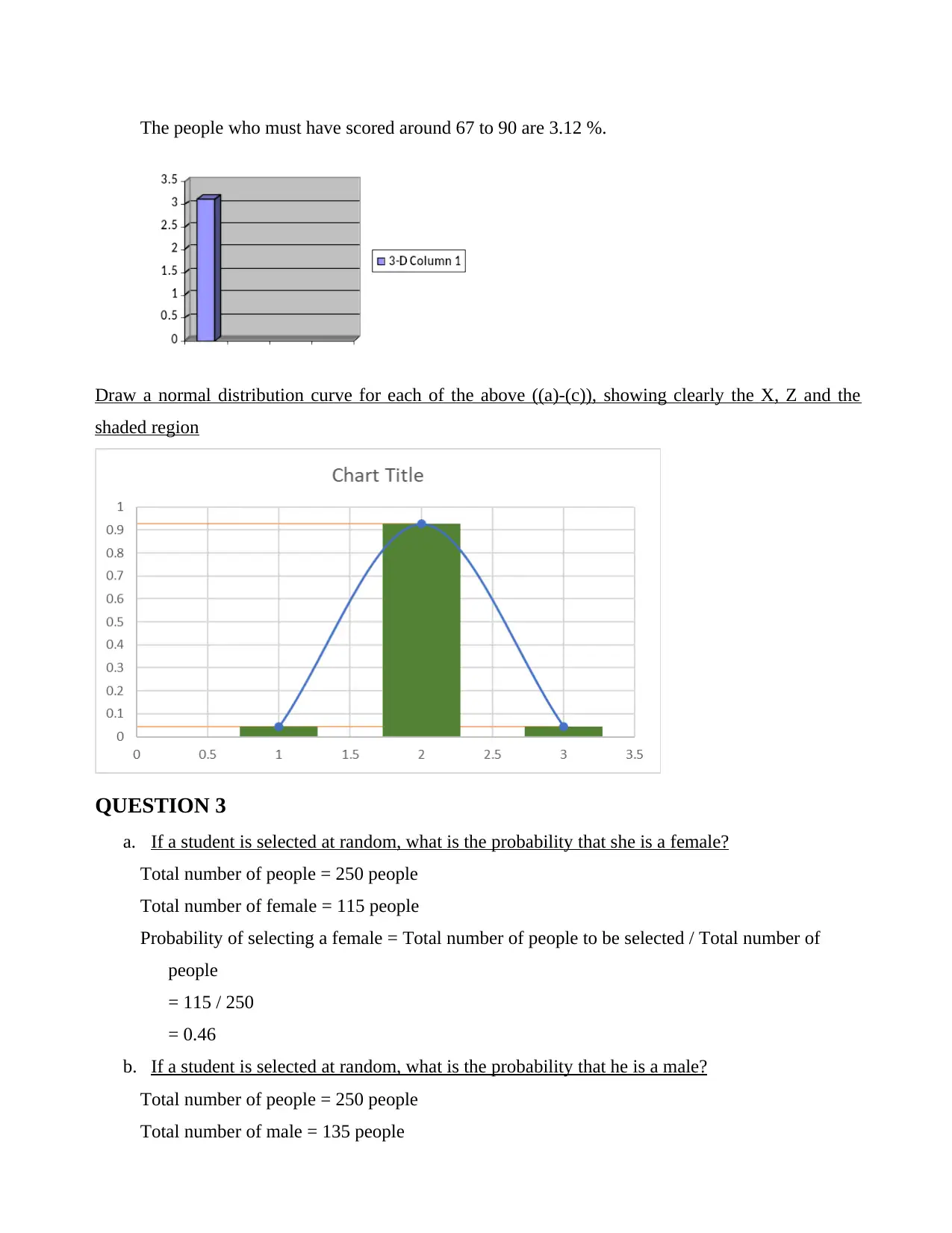
The people who must have scored around 67 to 90 are 3.12 %.
Draw a normal distribution curve for each of the above ((a)-(c)), showing clearly the X, Z and the
shaded region
QUESTION 3
a. If a student is selected at random, what is the probability that she is a female?
Total number of people = 250 people
Total number of female = 115 people
Probability of selecting a female = Total number of people to be selected / Total number of
people
= 115 / 250
= 0.46
b. If a student is selected at random, what is the probability that he is a male?
Total number of people = 250 people
Total number of male = 135 people

Probability of selecting a male = Total number of people to be selected / Total number of people
= 135 / 250
= 0.54
c. If a student is selected at random, what is the probability that he is a male or 25+ of age?
Total number of people = 250 people
Total number of male or 25+ of age = 20 people
Probability of selecting a male = Total number of people to be selected / Total number of people
= 20 / 250
= 0.08
d. If a student is selected at random, what is the probability that she is a female and age 17 - 25?
Total number of people = 250 people
Total number of female and age 17 - 25= 40 people
Probability of selecting a male = Total number of people to be selected / Total number of people
= 40 / 250
= 0.16
e. If a student is selected at random, what is the probability that she is a female given that she
is under 17 years old?
Total number of people = 250 people
Total number of female given that she is under 17 years old = 60 people
Probability of selecting a male = Total number of people to be selected / Total number of people
= 60 / 250
= 0.24
f. If a student is selected at random, what is the probability that student is 17-25 years old
given that the person is 25+ years old?
Total number of people = 250 people
Total number of female given that student is 17-25 years old given that the person is 25+ years
old = 90 + 35 = 125 people
Probability of selecting a male = Total number of people to be selected / Total number of people
= 125 / 250
= 0.5

QUESTION 4
a. Mode and Median
Mode is 12 as this test score is having the maximum frequency of 9. The higher occurring
frequency is always termed as mode which in this case is 12.
Median is the central figure of the table after sorting the intervals in ascending order.
Test Score Frequency Cum.F
4 8 8
10 7 15
12 9 24
15 6 30
16 5 35
Median = value of (N + 1/2) th item.
= (35 + 1) / 2
= 36 / 2
= 18 th item
Median = 12 which is the 18 the item in test score.
b. Mean to 2 decimal places
Test
Score Frequency x*f
4 8 32
10 7 70
12 9 108
15 6 90
16 5 80
Total 35 380
Mean = sum of x*f / Total frequency
= 380 / 35
= 10.85
c. Lower quartile and upper quartile
Lower quartile = (n + 1) / 4 th term
= (35 + 1) / 4
= 36 / 4
= 9 th item

Lower quartile = (n + 1) / 4 th term
= 10
Upper quatile = 3 / 4 (n + 1) th item
= 3 / 4 (35 + 1)
= 3 / 4 (36)
= 3* 9
= 27 th item
= 15
The lower quartile as per the calculations of Excel is 10 and the upper quartile is 15.
d. Range
Range = Upper value – lower value
= 16 – 4
= 12
e. Mean deviation to 2 decimal places
Test Score Frequency Cum.F x*f x - mean (x - mean)*f
4 8 8 32 6.857143 54.85714
10 7 15 70 0.857143 6
12 9 24 108 1.142857 10.28571
15 6 30 90 4.142857 24.85714
16 5 35 80 5.142857 25.71429
35 380 121.7143
3.477551
Mean deviation = (x - mean) *f / sum of f
= 121.7143 / 35
= 3.47
f. Sample variance and standard deviation to 2 decimal places
Test
Score Frequency Cum.F x*f x - mean
(x -
mean)*f
(x -
mean)^2
[(x -
mean)^2]f
4 8 8 32 6.857143 54.85714 47.02041 376.1633
10 7 15 70 0.857143 6 0.734694 5.142857
12 9 24 108 1.142857 10.28571 1.306122 11.7551

15 6 30 90 4.142857 24.85714 17.16327 102.9796
16 5 35 80 5.142857 25.71429 26.44898 132.2449
35 380 121.7143 628.2857
Standard deviation = √ 628.2857 / 35
= √ 17.95
= 4.23
Variance = Square of standard deviation
= (4.23) ^ 2
= 17.89
QUESTION 5
a. Define regression analysis
Regression Analysis of a data set determines which of the variable in the data set have
an impact on the topic of interest. It shows which of the factors in the series matter the most
and which can be ignored. It also shows how these factors have an influence on each other.
The two main variable considered in these are the dependent variable and the independent
variable (Stephens, 2017).
(b) Calculation of the regression equations:
1. b coefficient:
b = (Sxy / Sxx)
= 5.60647 / 4.61069
= 1.22
2. a coefficient:
a = y – bx
= 1.258 – 1.22* (2.025)
= 1.258 – 2.4705
= -1.21
3. Least square regression coefficients
Regression line

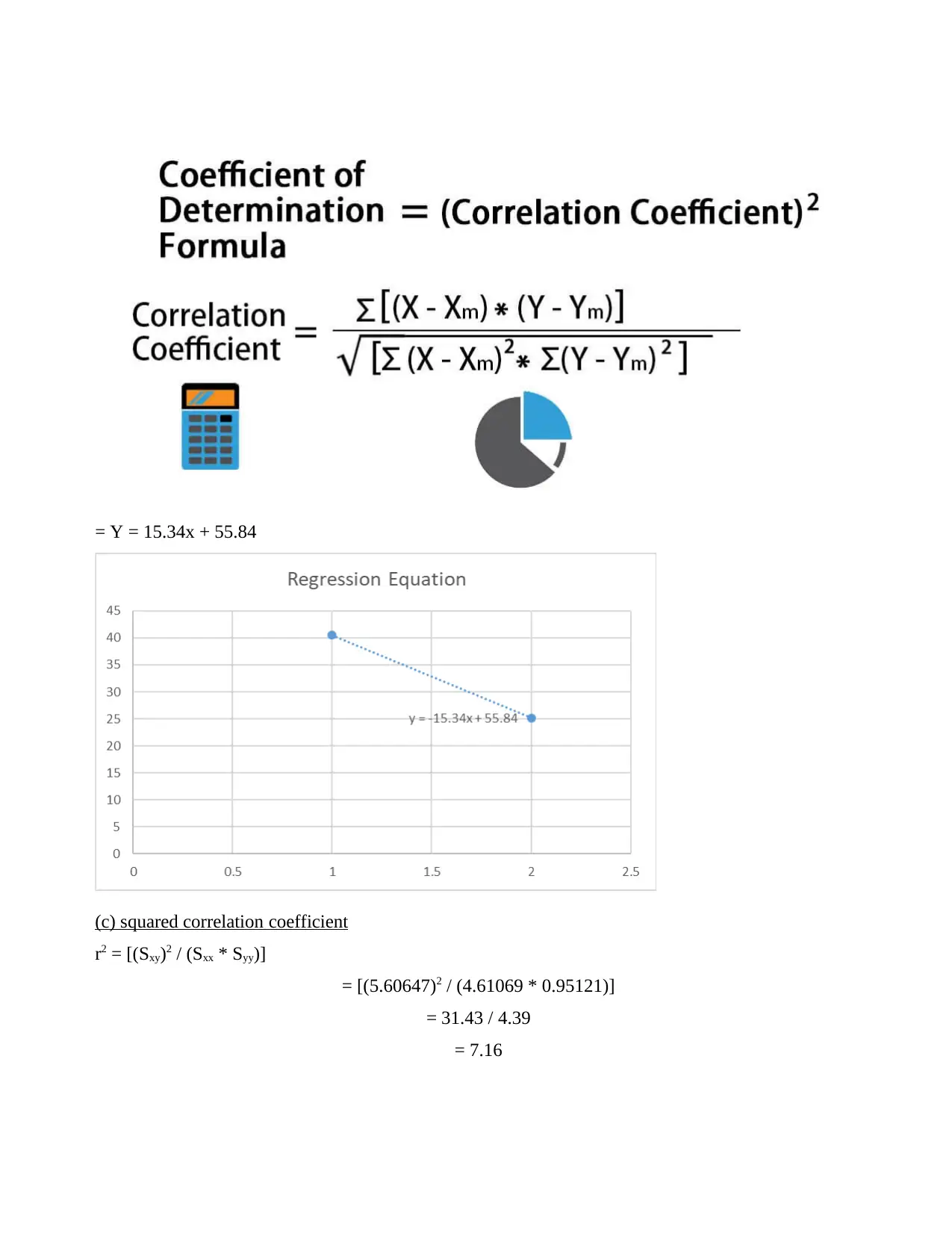
= Y = 15.34x + 55.84
(c) squared correlation coefficient
r2 = [(Sxy)2 / (Sxx * Syy)]
= [(5.60647)2 / (4.61069 * 0.95121)]
= 31.43 / 4.39
= 7.16