Report on Data Analysis and Linear Programming Application
VerifiedAdded on 2023/04/23
|7
|838
|160
Report
AI Summary
This document presents a student's solution to a data analysis and linear programming assignment. The analysis includes measures of central tendency and dispersion for advertising and sales data, revealing a strong positive correlation between the two variables. A regression model is formulated to predict sales revenue based on advertising expenditure, and the coefficient of determination indicates the model's explanatory power. Furthermore, the assignment addresses a linear programming problem aimed at maximizing laptop sales, determining the optimal quantity of PCs and laptops to sell within given constraints. The solution uses a graphical method to identify the extreme point that maximizes profit. Desklib provides access to a wealth of study resources, including past papers and solved assignments.

Data Analysis and Linear Programming 1
DATA ANALYSIS AND LINEAR PROGRAMMING
By (Name)
The Name of the Class (Course)
Professor (Tutor)
The Name of the School (University)
The City and State where it is located
The Date
DATA ANALYSIS AND LINEAR PROGRAMMING
By (Name)
The Name of the Class (Course)
Professor (Tutor)
The Name of the School (University)
The City and State where it is located
The Date
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Data Analysis and Linear Programming 2
Data Analysis and Linear Programming
Task 1
Part (a)
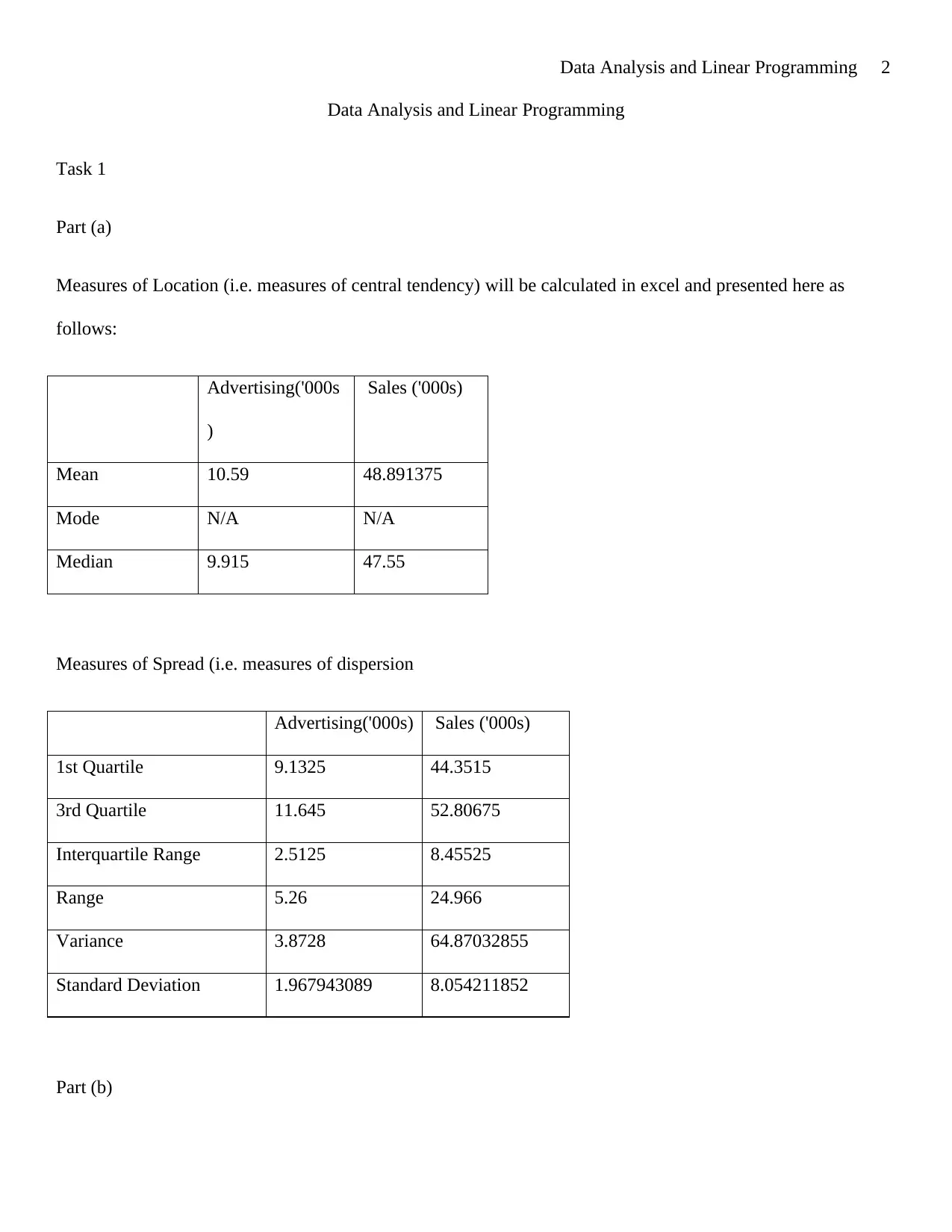
Measures of Location (i.e. measures of central tendency) will be calculated in excel and presented here as
follows:
Advertising('000s
)
Sales ('000s)
Mean 10.59 48.891375
Mode N/A N/A
Median 9.915 47.55
Measures of Spread (i.e. measures of dispersion
Advertising('000s) Sales ('000s)
1st Quartile 9.1325 44.3515
3rd Quartile 11.645 52.80675
Interquartile Range 2.5125 8.45525
Range 5.26 24.966
Variance 3.8728 64.87032855
Standard Deviation 1.967943089 8.054211852
Part (b)
Data Analysis and Linear Programming
Task 1
Part (a)
Measures of Location (i.e. measures of central tendency) will be calculated in excel and presented here as
follows:
Advertising('000s
)
Sales ('000s)
Mean 10.59 48.891375
Mode N/A N/A
Median 9.915 47.55
Measures of Spread (i.e. measures of dispersion
Advertising('000s) Sales ('000s)
1st Quartile 9.1325 44.3515
3rd Quartile 11.645 52.80675
Interquartile Range 2.5125 8.45525
Range 5.26 24.966
Variance 3.8728 64.87032855
Standard Deviation 1.967943089 8.054211852
Part (b)

Data Analysis and Linear Programming 3
The Product-moment correlation coefficient (i.e. Pearson correlation coefficient) is indicated in the tables
below. According to the result, there is a very strong positive relationship (0.947159) between advertising
expenditure and sales revenue. Therefore, there follow the same pattern if one is increasing the other is also
increasing; likewise, if one is decreasing the other is also decreasing.
Advertising('000s) Sales ('000s)
Advertising('000s) 1
Sales ('000s) 0.947159454 1
Part (c)
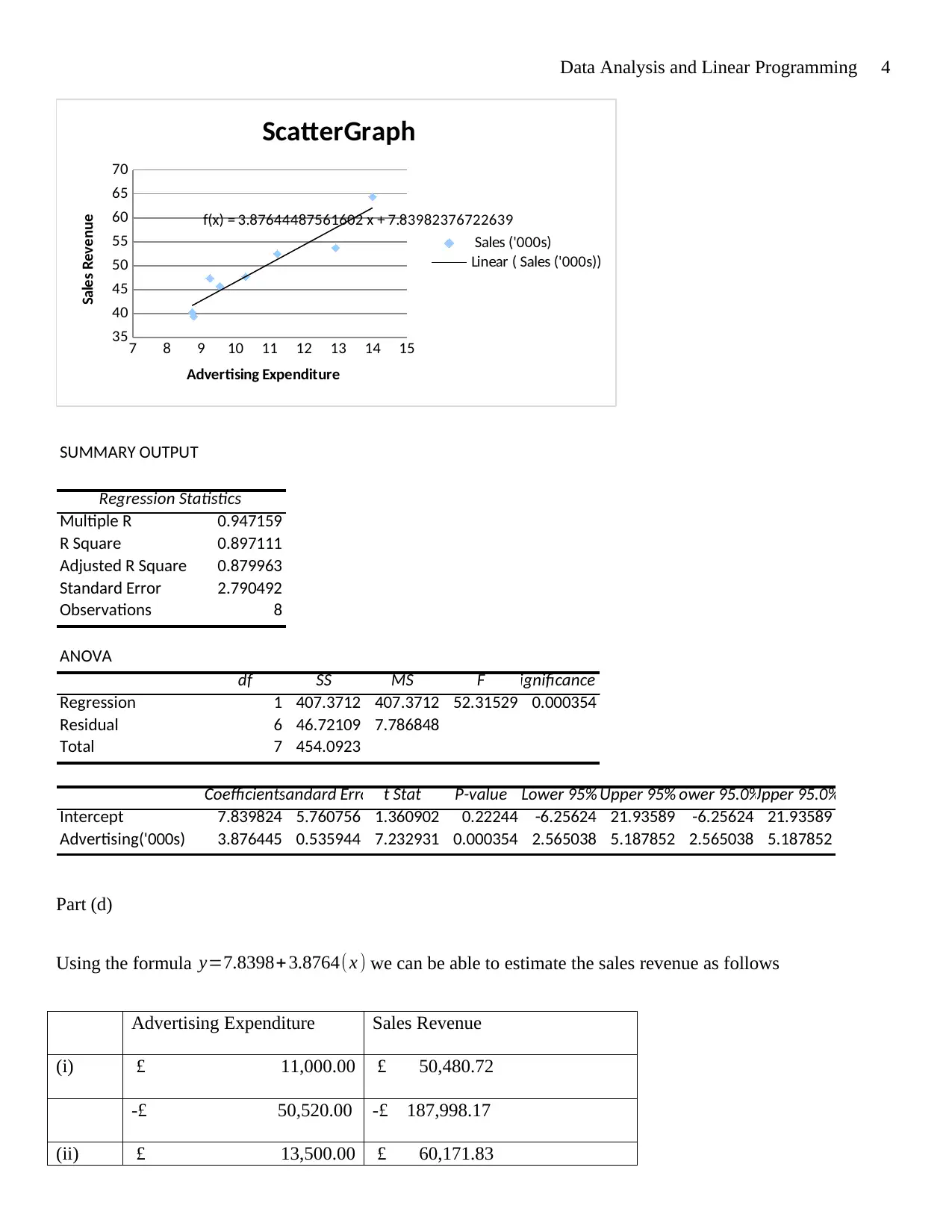
From the regression output below, we can formulate the relation between advertising expenditure (x) and sales
revenue (y) as follows:
y=7.8398+3.8764(x )
Where a=7.8398 and b=3.8764
We can interpret “a” to represent the intercept; therefore, when advertising expenditure is £0, the sales revenue
will be £7,839.80. On the other hand, “ b” represents the slope and as a result an increment in advertising
expenditure by 1 unit (£1,000) will increase sales revenue by £3,876.40 (Montgomery 2013).
The Product-moment correlation coefficient (i.e. Pearson correlation coefficient) is indicated in the tables
below. According to the result, there is a very strong positive relationship (0.947159) between advertising
expenditure and sales revenue. Therefore, there follow the same pattern if one is increasing the other is also
increasing; likewise, if one is decreasing the other is also decreasing.
Advertising('000s) Sales ('000s)
Advertising('000s) 1
Sales ('000s) 0.947159454 1
Part (c)
From the regression output below, we can formulate the relation between advertising expenditure (x) and sales
revenue (y) as follows:
y=7.8398+3.8764(x )
Where a=7.8398 and b=3.8764
We can interpret “a” to represent the intercept; therefore, when advertising expenditure is £0, the sales revenue
will be £7,839.80. On the other hand, “ b” represents the slope and as a result an increment in advertising
expenditure by 1 unit (£1,000) will increase sales revenue by £3,876.40 (Montgomery 2013).
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Data Analysis and Linear Programming 4
7 8 9 10 11 12 13 14 15
35
40
45
50
55
60
65
70
f(x) = 3.87644487561602 x + 7.83982376722639
ScatterGraph
Sales ('000s)
Linear ( Sales ('000s))
Advertising Expenditure
Sales Revenue
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.947159
R Square 0.897111
Adjusted R Square 0.879963
Standard Error 2.790492
Observations 8
ANOVA
df SS MS F Significance F
Regression 1 407.3712 407.3712 52.31529 0.000354
Residual 6 46.72109 7.786848
Total 7 454.0923
CoefficientsStandard Error t Stat P-value Lower 95% Upper 95%Lower 95.0%Upper 95.0%
Intercept 7.839824 5.760756 1.360902 0.22244 -6.25624 21.93589 -6.25624 21.93589
Advertising('000s) 3.876445 0.535944 7.232931 0.000354 2.565038 5.187852 2.565038 5.187852
Part (d)
Using the formula y=7.8398+ 3.8764( x ) we can be able to estimate the sales revenue as follows
Advertising Expenditure Sales Revenue
(i) £ 11,000.00 £ 50,480.72
-£ 50,520.00 -£ 187,998.17
(ii) £ 13,500.00 £ 60,171.83
7 8 9 10 11 12 13 14 15
35
40
45
50
55
60
65
70
f(x) = 3.87644487561602 x + 7.83982376722639
ScatterGraph
Sales ('000s)
Linear ( Sales ('000s))
Advertising Expenditure
Sales Revenue
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.947159
R Square 0.897111
Adjusted R Square 0.879963
Standard Error 2.790492
Observations 8
ANOVA
df SS MS F Significance F
Regression 1 407.3712 407.3712 52.31529 0.000354
Residual 6 46.72109 7.786848
Total 7 454.0923
CoefficientsStandard Error t Stat P-value Lower 95% Upper 95%Lower 95.0%Upper 95.0%
Intercept 7.839824 5.760756 1.360902 0.22244 -6.25624 21.93589 -6.25624 21.93589
Advertising('000s) 3.876445 0.535944 7.232931 0.000354 2.565038 5.187852 2.565038 5.187852
Part (d)
Using the formula y=7.8398+ 3.8764( x ) we can be able to estimate the sales revenue as follows
Advertising Expenditure Sales Revenue
(i) £ 11,000.00 £ 50,480.72
-£ 50,520.00 -£ 187,998.17
(ii) £ 13,500.00 £ 60,171.83
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Data Analysis and Linear Programming 5
-£ 60,220.00 -£ 225,599.69
(iii) £ 15,000.00 £ 65,986.50
-£ 66,040.00 -£ 248,160.60
Part (e)
The coefficient of determination also referred to as R-squared is 0.89711. The coefficient indicates that 89.71%
of the change in sales revenue (dependent variable) can be explained by advertising expenditure (independent
variable).
Part (f)
Yes, the relationship is sufficiently strong because the coefficient of determination is considerably close to 1. A
value of 1 indicates that 100% of the change in the dependent variable is explained by the independent variable.
(NB: the value of significance F (0.000354) in the regression output above is considerably smaller than alpha of
0.05. indicating that the model is statistically significant)
Task 2
Maximization of Laptop Sales
The research question here is:
How many laptops and PCs should be sold in order to maximize profits?
The variables in this problem are
(i) Quantity of PCs i.e. X
-£ 60,220.00 -£ 225,599.69
(iii) £ 15,000.00 £ 65,986.50
-£ 66,040.00 -£ 248,160.60
Part (e)
The coefficient of determination also referred to as R-squared is 0.89711. The coefficient indicates that 89.71%
of the change in sales revenue (dependent variable) can be explained by advertising expenditure (independent
variable).
Part (f)
Yes, the relationship is sufficiently strong because the coefficient of determination is considerably close to 1. A
value of 1 indicates that 100% of the change in the dependent variable is explained by the independent variable.
(NB: the value of significance F (0.000354) in the regression output above is considerably smaller than alpha of
0.05. indicating that the model is statistically significant)
Task 2
Maximization of Laptop Sales
The research question here is:
How many laptops and PCs should be sold in order to maximize profits?
The variables in this problem are
(i) Quantity of PCs i.e. X

Data Analysis and Linear Programming 6
(ii) Quantity of Laptops i.e. Y
Maximization Problem Expression
Max z=400 x +700 y where x=quantity o f PCs∧ y=quantity of laptops
Constraints Expression
1000 x+1500 y ≤100,000
x ≥ 15
x ≤ 80
y ≥0
y ≤ 40
(Sultan 2014)
The Graphical Solution
Using an online graphing tool the objective function z is maximized (Z=$44,000) at the extreme point (40, 40)
hence x=40, and y=40.
Hence quantity of laptops that should be sold to maximize profit is 40.
(ii) Quantity of Laptops i.e. Y
Maximization Problem Expression
Max z=400 x +700 y where x=quantity o f PCs∧ y=quantity of laptops
Constraints Expression
1000 x+1500 y ≤100,000
x ≥ 15
x ≤ 80
y ≥0
y ≤ 40
(Sultan 2014)
The Graphical Solution
Using an online graphing tool the objective function z is maximized (Z=$44,000) at the extreme point (40, 40)
hence x=40, and y=40.
Hence quantity of laptops that should be sold to maximize profit is 40.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Data Analysis and Linear Programming 7
References
Montgomery, C., 2013. Introduction to Linear Regression Analysis. Hoboken: John Wiley & Sons.
Sultan, A., 2014. Linear Programming: An Introduction with Applications. Amsterdam: Elsevier.
References
Montgomery, C., 2013. Introduction to Linear Regression Analysis. Hoboken: John Wiley & Sons.
Sultan, A., 2014. Linear Programming: An Introduction with Applications. Amsterdam: Elsevier.
1 out of 7
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





