Numeracy & Data Analysis: Wind Speed Forecasting in London

This report examines wind speed data using numeracy and data analysis techniques to facilitate future forecasting. It employs various methods, including calculating mean, median, mode, standard deviation, and range, to analyze the data. The report also utilizes a linear forecasting model to predict future wind speeds in London, considering past values. Specifically, it forecasts wind speeds for Day 11 and Day 13 using the linear forecasting model, providing insights into potential future trends based on historical data. The analysis is supported by charts and graphs to enhance understanding and reliability.

Numeracy and Data
Analysis

Contents
Contents...........................................................................................................................................2
INTRODUCTION...........................................................................................................................3
MAIN BODY/TASKS.....................................................................................................................3
1. Arrange the data -....................................................................................................................3
2.Data of wind speed of city London are described in following charts -...................................3
3.There are various methods of data analysis for assessment which are as follows -.................5
4. Evaluate the value of m and c with the use of linear forecasting model which is y = mx + c.7
CONCLUSION................................................................................................................................9
REFERENCES................................................................................................................................1

INTRODUCTION
In this report, the wind speed of country is examined through numeracy and data analysis
to collect the information for better future forecasting. There are different methods to analyse the
data, but in numeracy data is calculated with the use of mean, median, mode, standard deviation
and range. We also use linear forecasting model for London to get the idea of future events with
consideration of past values. Here, we are also predicting the wind speed of Day 11 and Day 13
with the help of linear forecasting model (Hillier, 2009).
MAIN BODY/TASKS
1. Arrange the data -
Day Wind
Speed
1 7
2 2
3 4
4 5
5 6
6 5
7 5
8 16
9 8
10 14
Total 72
2.Data of wind speed of city London are described in following charts -

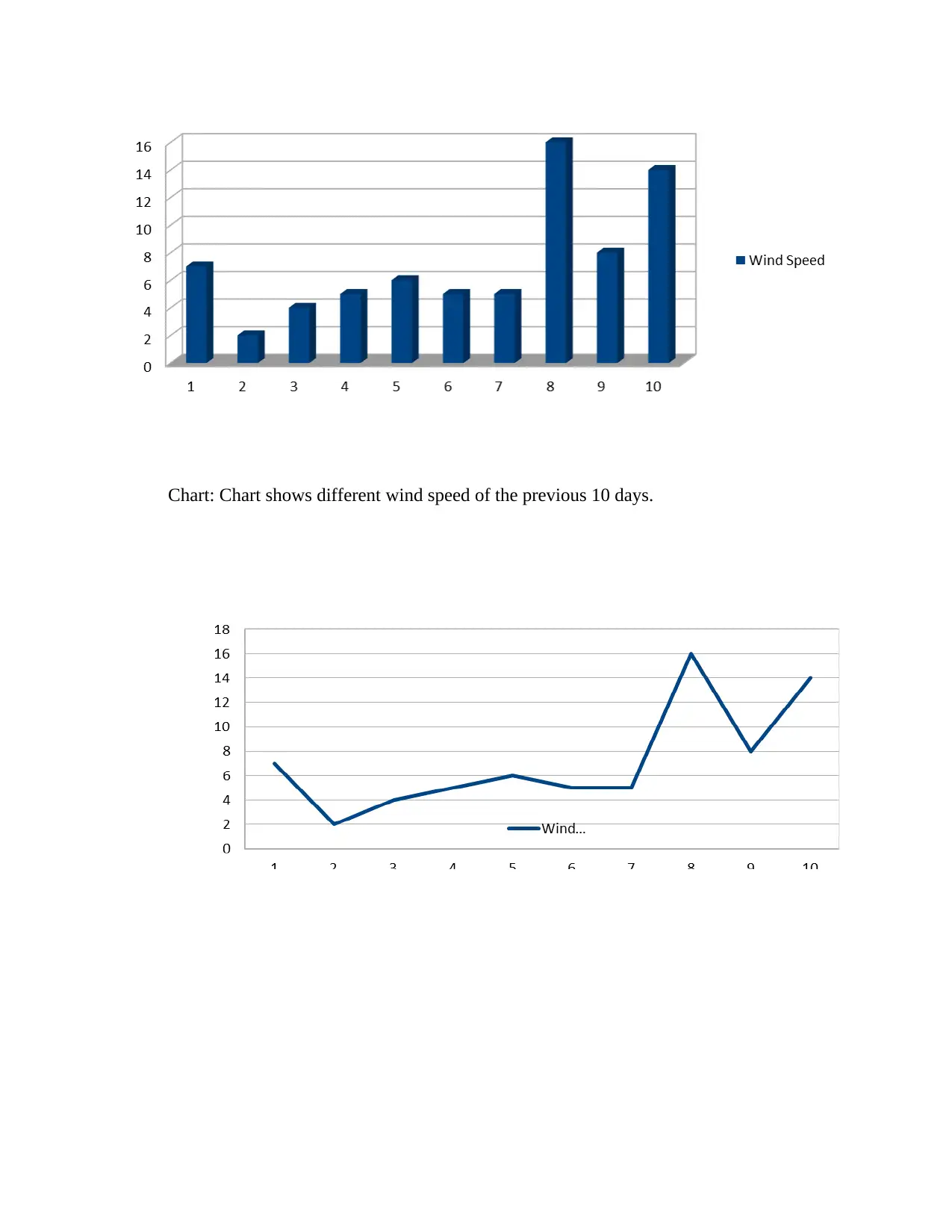
Chart: Chart shows different wind speed of the previous 10 days.

3.There are various methods of data analysis for assessment which are as follows -
Mean - Mean is the method which summarized as an entire dataset with a single number
representing the data's centre point. This helps to assess the performance of an investment or
company over a period of time. It refers as summing the numbers in a set and dividing by the
total numbers gives us the arithmetic mean (Irwin and Britt, 2005).
Following are the steps which are considered for calculating mean -
Step 1: Firstly, gather the given data.
Step 2: Calculate the sum of data.
Step 3: Then, count the number of values in the data set.
Step 4: After that, divide the sum of the data set by the number of values.
Mean of Wind Speed = Sum of all observations / Total number of observations
Mean = 72 / 10
Mean = 7.2
Median – Median is the middle value of the given observations, when arranged in an
order. The arrangement of data can be either done in ascending or descending order. Median
formula is
These are the steps which is to be followed for calculating median -
Step 1: Arrange the observations in numerical order.
Step 2: Now, count how many numbers we have.
Step 3: If the number of observations are odd in number, divide the number by 2 and round up to
get the position of the median number.
Median = N + 1 / 2
Step 4: If the number of observations are even in number, divide it by 2. Go to the number in that
position and do average of it with the number in the next higher position for finding the median.
Median = N / 2
Median of wind speed of London is as follows:
7, 2, 4, 5, 6, 5, 5, 16, 8, 14
2, 4, 5, 5, 5, 6, 7, 8, 14, 16
Median = (10 + 1) / 2

Median = 5.5th position
Median = (5+6) / 2
Median = 5.5
Mode - Mode is one of the statistical measures of central tendency in a set of data.
It is the result which occurs maximum times or has the highest frequency in the given data set.
Steps for the calculation of mode by using observations are (Lee and Choi,2020)-
Step 1: Firstly, arranging the data of numbers in ascending or descending order.
Step 2: Determine all the distinct values in a dataset.
Step 3: Then, count the frequency of occurrence for every different value.
Step 4: Now, the value which comes more is the mode.
2, 4, 5, 5, 5, 6, 7, 8, 14, 16
Mode = 5
Range – Range is a statistical measurement of dispersion in which we calculate the
difference between the greatest and smallest value.
There are some steps for the calculation of the range -
Step 1: Gather the data and arrange it in systematic way.
Step 2: Then, consider the highest and the lowest value.
Step 3: Find the difference between highest and lowest value.
Step 4: After this, the value obtained is range.
Calculation of wind speed range:
Range = Highest value – Lowest value
= 16 – 2
Range = 14
Standard Deviation – The average amount of changeability in the set of data. It is
a useful method of spread for standard distributions (Kortjass and et.al., 2020).
Few steps of calculating standard deviation are given here:
Step 1: Firstly, find the value of mean.
Step 2: Now, find each observation's deviation from the mean.
Step 3: Then, squaring the observation's deviation from the mean.
Step 4: Calculate the sum of squares.
Step 5: Then, find the variance by dividing the sum of squares by number of observations.

Step 6: After calculating these values, take a square root of the value comes in step 5.
Calculation of wind speed's standard deviation:
Standard Deviation = √∑ (xi – μ) 2 / N
= √45067.6 / 10
Standard Deviation = 21.22.
4. Evaluate the value of m and c with the use of linear forecasting model which is y = mx + c.
Linear Forecasting Model - This model is useful in forecasting for future decisions
with the help of past data (Rima, 1994).
Steps of calculating linear forecasting model are given as follows:
Step 1: Firstly, find out the definition of problem.
Step 2: Gathering the information.
Step 3: Find out the information from preliminary.
Step 4: Select and fit the model according to the information.
Step 5: Now, do careful analysis of information.
y = mx + c
where, 'y' is referring to Dependent Factor
'mx' refers to Independent factor and
'c' refers to Constant Factor
The following are the values of ‘m’:
Step 1: Find the sum up of total number and then multiply both the term and the count of total
number.
Step 2: Computing the sum of 'x' and 'y' variable terms individually.
Step 3: Then deduct the step 2 from step 1.
Step 4: Calculate the squares of each value of x and do multiplication with the total number of
terms.
Step 5: Then compute the squares of sum of 'x'.
Step 6: Deduct the step 5 from step 4.
Step 7: At last, divide the value of step 3 with step 6.

m = 10*478 – 55*72 / 10*385 – 55*55
m = 0.99
There are few steps for computation of 'c':
Step 1: Firstly, do the sum of 'y' variable.
Step 2: Then, compute the value of 'm'.
Step3: Compute the sum of 'x' variable and then multiply both 'm' and sum of 'x'
Step4: Subtracting the total of 'mx' from total of 'y'
Step5: After that divide the value of Step4 by 'n'
c = 72 – 0.99*55 / 10
c = 1.755
Wind Speed on Day 11:
m = 0.99, c = 1.755, x = 11
y = mx + c
= 0.99*11 + 1.755
y = 12.645
Wind Speed on Day 13:
m = 0.99, c = 1.755, x = 13
y = mx + c
= 0.99*13 + 1.755
y = 14.625

CONCLUSION
From the above prepared report, it can be concluded that mean, median, mode is helpful in
assessment and enumeration of data. The data which is considered here is of wind speed of
London for 10 consecutive days. The information which is collected here is described on the
basis of charts and graphs as well that makes it more reliable and easy to forecast future events
and outcomes.

REFERENCES
Hillier, Y., 2009. The changing faces of adult literacy, language and numeracy: Literacy policy
and implementation in the UK. Compare. 39(4). pp.535-550.
Irwin, K.C. and Britt, M.S., 2005. The algebraic nature of students’ numerical manipulation in
the New Zealand Numeracy Project. Educational Studies in Mathematics. 58(2). pp.169-
188.
Kortjass and et.al., 2020 Teacher educators of numeracy. Glimpses into Primary School Teacher
Education in South Africa, p.104.
Lee, H.K. and Choi, A., 2020. Enhancing early numeracy skills with a tablet-based math game
intervention: a study in Tanzania. Educational Technology Research and
Development. 68(6). pp.3567-3585.
Rima, I.H., 1994. The role of numeracy in the history of economic analysis. Journal of the
History of Economic Thought. 16(2). pp.188-201.
1