Data Analysis Report: Monthly Bill Data and Linear Forecasting

This report presents a comprehensive data analysis of monthly printed bills over a 12-month period. It begins with an introduction outlining the objectives and methodologies employed. The report details the data collection process and presents the data using column and bar charts for visualization. Descriptive statistical methods such as mean, median, mode, range, and standard deviation are calculated and interpreted to provide insights into the central tendency, dispersion, and variability of the bill amounts. Furthermore, a linear forecasting model is developed to predict future expenses, with calculations for the slope (m) and intercept (c) values. The report concludes with an assessment of the model's efficiency and suggests the use of more advanced statistical tools for improved data prediction. References to relevant statistical literature are also included.

Data Analysis

Table of Contents
Introduction......................................................................................................................................3
Data Collection............................................................................................................................3
Data Presentation.........................................................................................................................4
Calculation...................................................................................................................................4
Linear forecasting model.............................................................................................................6
Conclusion.......................................................................................................................................8

Introduction
The following report is based on data analyses techniques to extract useful information from
given data. In this report, the data of past 12 months printed bills have been taken. For
descriptive analyses; mean, median, mode, range and standard deviation have been applied as
statistical method.
Data Collection
Mont
h Bill (£)
1 1250
2 1100
3 1400
4 1600
5 1300
6 1200
7 750
8 850
9 1000
10 1050
11 780
12 900

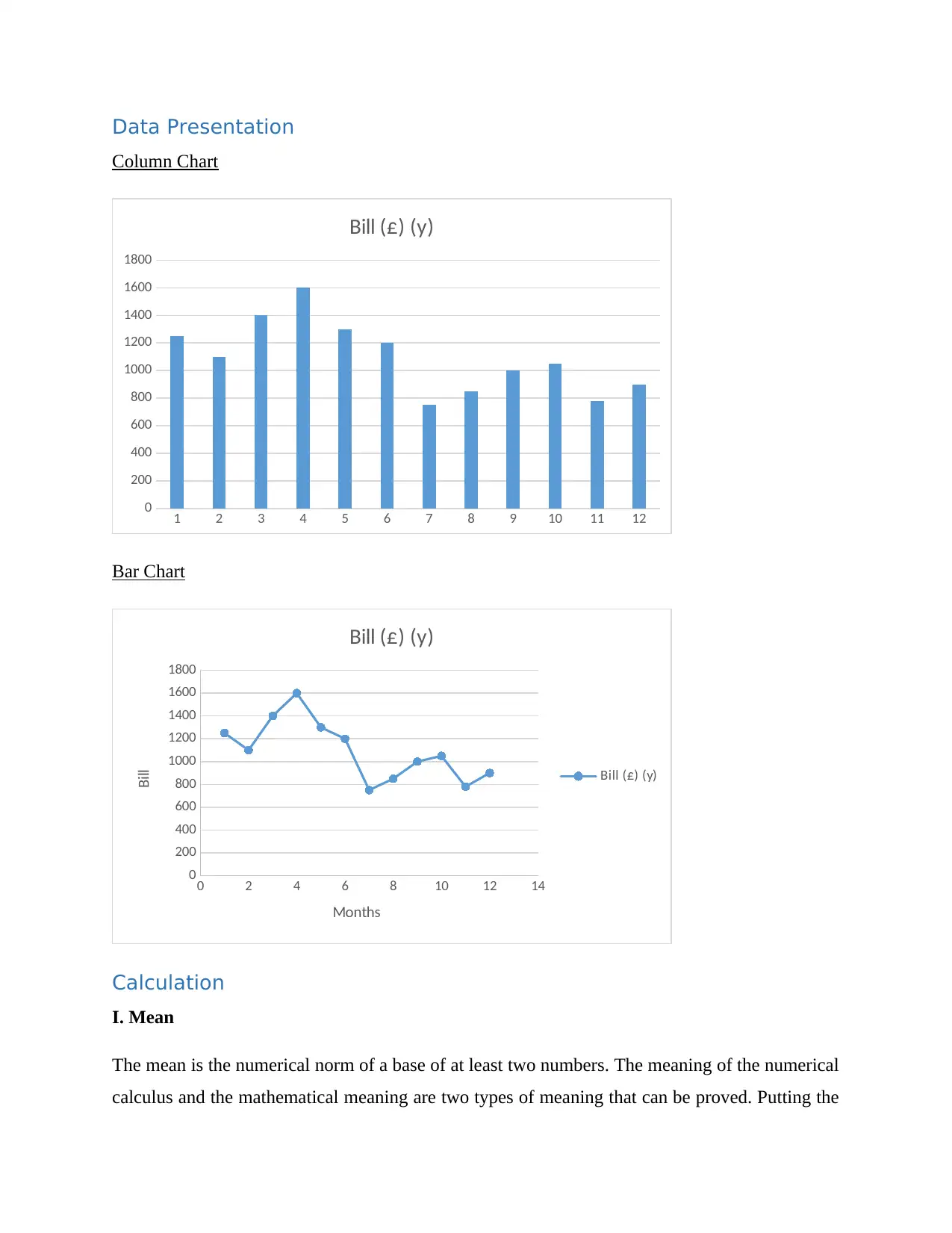
Data Presentation
Column Chart
1 2 3 4 5 6 7 8 9 10 11 12
0
200
400
600
800
1000
1200
1400
1600
1800
Bill (£) (y)
Bar Chart
0 2 4 6 8 10 12 14
0
200
400
600
800
1000
1200
1400
1600
1800
Bill (£) (y)
Bill (£) (y)
Months
Bill
Calculation
I. Mean
The mean is the numerical norm of a base of at least two numbers. The meaning of the numerical
calculus and the mathematical meaning are two types of meaning that can be proved. Putting the

numbers into a set and dividing them by the number gives you mathematical meaning. In science
and insights, the mathematical meaning, or simply the mean or the mean, is the number of
numbers separated by the inclusion of the numbers in the field. Assortment is consistently the
basis of analytical or subjective analysis results, or often includes a handful of results from an
overview (Ranganathan, Pramesh and Aggarwal, 2017).
Mean = ∑ total of bill
No of months
Mean = 1250+1100+1400+1600+1300+1200+750+850+ 1000+ 1050+780+900
12
Mean = ¿ 1250+1100+1400+1600+1300+1200+750+850+1000+ 1050+750+900 13180
12 =
£1098.33
The result shows that the average expense incurred on printing bill is equivalent to £1098.33. It
also indicates that on an average £1098.33has been spent for payment of bill within 12 months.
II. Median
In probabilistic visions and hypotheses, it is worth separating the upper half from the lower half
of a test of information, population, or appearance behavior. For information index, it could be
regarded as "the center" of respect (Fagerland, Lydersen and Laake, 2017). The medium is
invaluable for highlighting things like compensation, where big figures can make sense. The
median salary in the United States as of 2012 was $ 51,017. On the off chance of being used,
these wealthy Americans could raise that figure.
Mont
h Bill (£)
1 750
2 780
3 850
4 900
5 1000
6 1050
7 1100
8 1200

9 1250
10 1300
11 1400
12 1600
Median = (5th value + 6th value)/2
= (1000 + 1050)/2
= (2050)/2 = £1025
The value of median is the indication of mid-point the raw data after sorting it in ascending
order.
III. Mode
The mode is the value that appears regularly in a group of information sources. Since X is not a
separate nonlinear variable, the method is the value of x whose mass potential is most likely to
achieve the maximum value. Overall, it's worth it and well on your way to exploration. The
method of indexing information is the number that is usually found in the set. To find the method
manually, sort the numbers from the smallest to the most obvious and quickly determine how
often each number occurs (Yi, 2017). It is the maximum number that will occur. If there are two
numbers appearing frequently (and the same number of times) then, at that point the information
has two ways. This is called bimodal. If there are no more than 2, the information would be
complex. As not all numbers appear to be identical multiple times, information gathering is non-
existent (Xia, Sun and Chen, 2018).
No bill has repeated within 12 months; thus the value of mode will be Nil.
IV. Range
In arithmetic, the range of data can be related to the two closely related ideas: The range of
ability The image of ability Gives two sets of X and Y, a double relation f between X and Y is
ability if it is for every x into X ay is generally in Y with the final objective relating x to y (Little
and Rubin, 2019). Specifically, the area of the spread is an estimate of reality, or the extent to
which a particular index of information is released from the smallest to the largest. In a source of

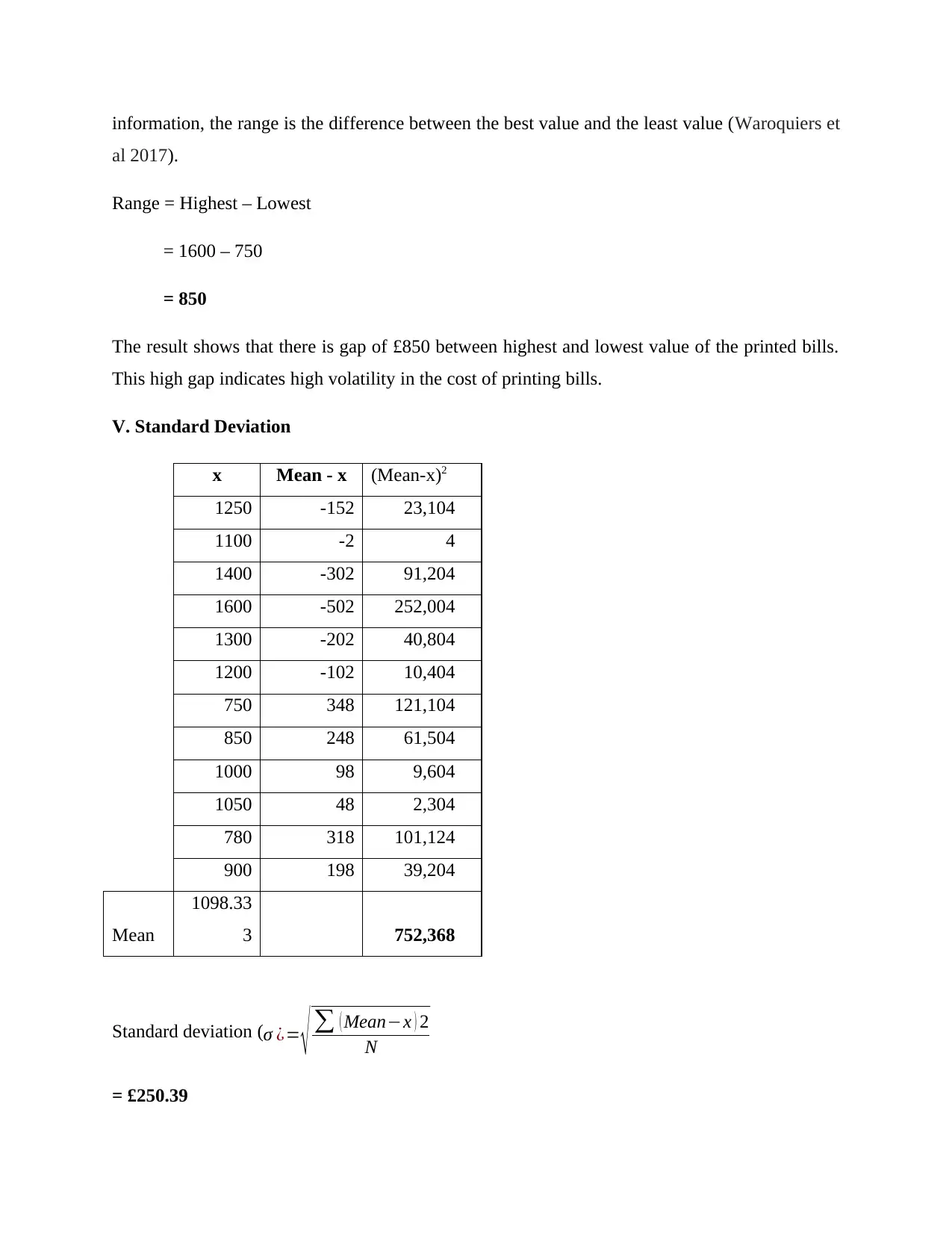
information, the range is the difference between the best value and the least value (Waroquiers et
al 2017).
Range = Highest – Lowest
= 1600 – 750
= 850
The result shows that there is gap of £850 between highest and lowest value of the printed bills.
This high gap indicates high volatility in the cost of printing bills.
V. Standard Deviation
x Mean - x (Mean-x)2
1250 -152 23,104
1100 -2 4
1400 -302 91,204
1600 -502 252,004
1300 -202 40,804
1200 -102 10,404
750 348 121,104
850 248 61,504
1000 98 9,604
1050 48 2,304
780 318 101,124
900 198 39,204
Mean
1098.33
3 752,368
Standard deviation (σ ¿= √ ∑ ( Mean−x ) 2
N
= £250.39

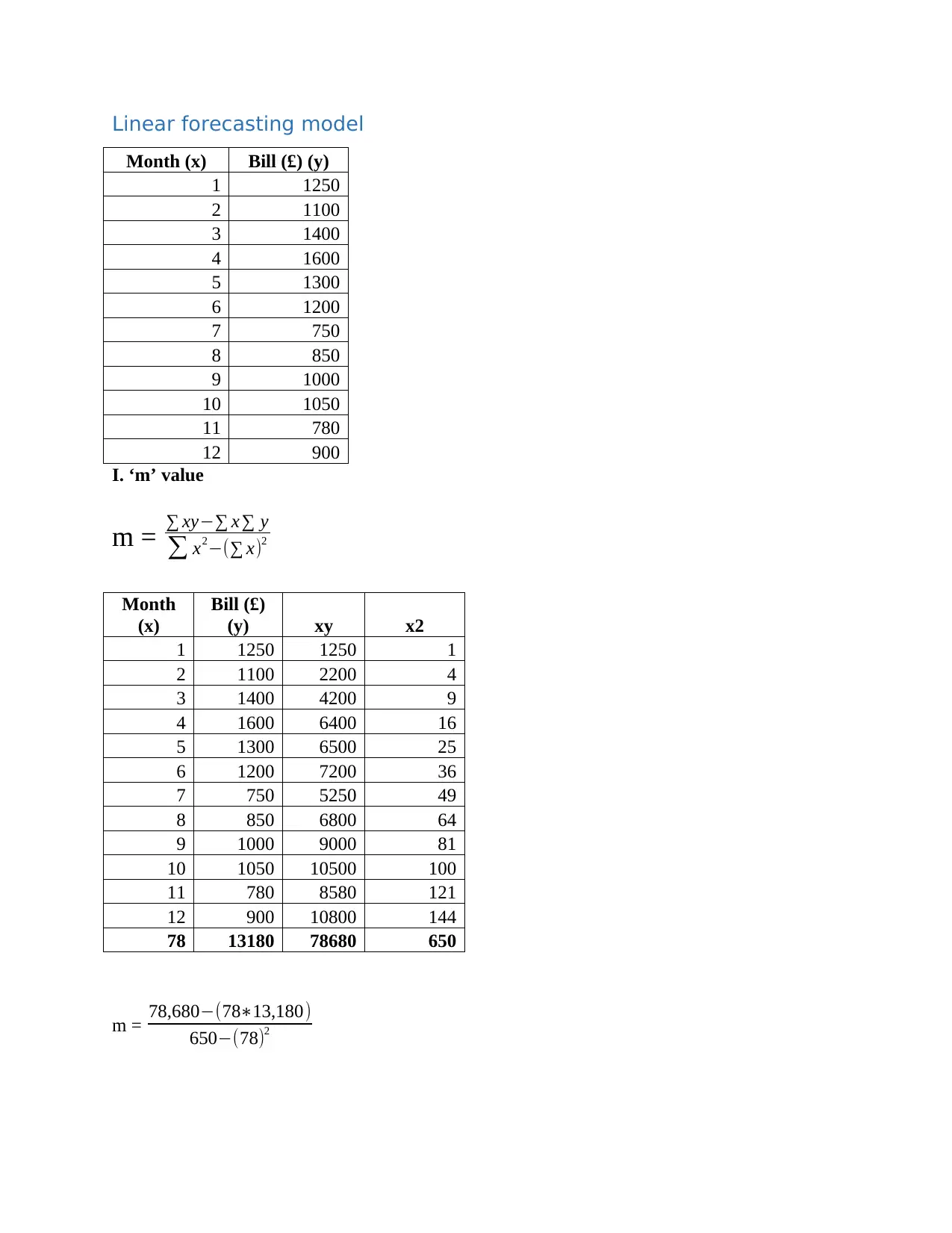
Linear forecasting model
Month (x) Bill (£) (y)
1 1250
2 1100
3 1400
4 1600
5 1300
6 1200
7 750
8 850
9 1000
10 1050
11 780
12 900
I. ‘m’ value
m = ∑ xy−∑ x ∑ y
∑ x2−(∑ x)2
Month
(x)
Bill (£)
(y) xy x2
1 1250 1250 1
2 1100 2200 4
3 1400 4200 9
4 1600 6400 16
5 1300 6500 25
6 1200 7200 36
7 750 5250 49
8 850 6800 64
9 1000 9000 81
10 1050 10500 100
11 780 8580 121
12 900 10800 144
78 13180 78680 650
m = 78,680−(78∗13,180)
650−(78)2

= ¿ 78680−(78∗13180)−949360
¿650−( 78∗78)−5434
= 174.71
The value of m indicates the slope of given variables. Positive slope indicates that any increase
or decrease in independent variable has direct impact on dependent variable. The above slope
shows that any increase or decrease in months multiplies the month by 174.71 times to get the
result in the form of printed bill.
II. c value
c = ∑ y−m ∑ x
N
c = 13180−174.71 ( 78 )
12
c = -37.28
The value of c is also known as constant and intercept. This intercept is the expected mean value
of y which best use for predicting the value of y based on the input in the form of x value.
III. Forecasting of the expenses
Month 12th:
y = mx + c
= 174.71 (12) – 37.28
y = £2059.24
Month 14th
y = 174.71 (14) – 37.28
= £2408.66

Conclusion
Based on above data it can be concluded that regression analysis is not efficient enough to give
accurate data prediction. Thus it is necessary to consider other advanced statistical tool such as
exponential regression analysis to get more accurate data.

References
Fagerland, M., Lydersen, S. and Laake, P., 2017. Statistical analysis of contingency tables. CRC
press.
Little, R.J. and Rubin, D.B., 2019. Statistical analysis with missing data (Vol. 793). John Wiley
& Sons.
Ranganathan, P., Pramesh, C.S. and Aggarwal, R., 2017. Common pitfalls in statistical analysis:
logistic regression. Perspectives in clinical research, 8(3), p.148.
Waroquiers, D., Gonze, X., Rignanese, G.M., Welker-Nieuwoudt, C., Rosowski, F., Göbel, M.,
Schenk, S., Degelmann, P., André, R., Glaum, R. and Hautier, G., 2017. Statistical analysis of
coordination environments in oxides. Chemistry of Materials, 29(19), pp.8346-8360.
Xia, Y., Sun, J. and Chen, D.G., 2018. Statistical analysis of microbiome data with R (Vol. 847).
Singapore: Springer.
Yi, G.Y., 2017. Statistical analysis with measurement error or misclassification: strategy,
method and application. Springer.