Data Mining Report: Classification Algorithms Performance Analysis

This report presents a data mining evaluation of the performance of different classification algorithms, including Decision Tree, Naive Bayes, and k-Nearest Neighbor (KNN). The dataset (vote.arff) was loaded into Weka, and the performance of each algorithm was compared based on the number of correctly and incorrectly classified attributes. The Decision Tree algorithm achieved the highest performance with 98.2759% accuracy, followed by KNN at 93.5484% and Naive Bayes at 91.4474%. The analysis concludes that the Decision Tree is the most suitable classifier for the dataset used in this evaluation.

Data mining and visualization
Student Name:
Instructor Name:
Course Number:
8 September 2018

Introduction
The aim of this report is to present analysis of a data mining evaluation of the performance of
different classification algorithms. The data set (vote.arff) was loaded into Weka and comparison
of the performance on the data set for three classification algorithms was peformed. The three
different classigfication algorithms include:
 Decision Tree
 Naive Bayes
 k-Nearest Neighbour (KNN)
Decision Tree
A decision tree refers to a classifier that is given as a recursive slit-up of the case space. The
decision tree comprises of nodes that shape an established tree, which means it is a coordinated
tree with a node called "root" that has no approaching edges (Kamiński, Jakubczyk, & Szufel,
2017). Every single other node have precisely one approaching edge. A node with active edges is
called an interior or test node. In this section, we sought to perform a data mining algorithm
which is based on classification using Decision Tree approach. Using a 60% split where 60% in
the training set and 40% in the testing test, we ran a decision tree test. The results as can be seen
in the screenshot given below (figure 1) showed that 171 attributes were correctly identified
using this methodology while only 3 attributes were incorrectly classified. This gives the
approach a performance percentage of 98.2759%

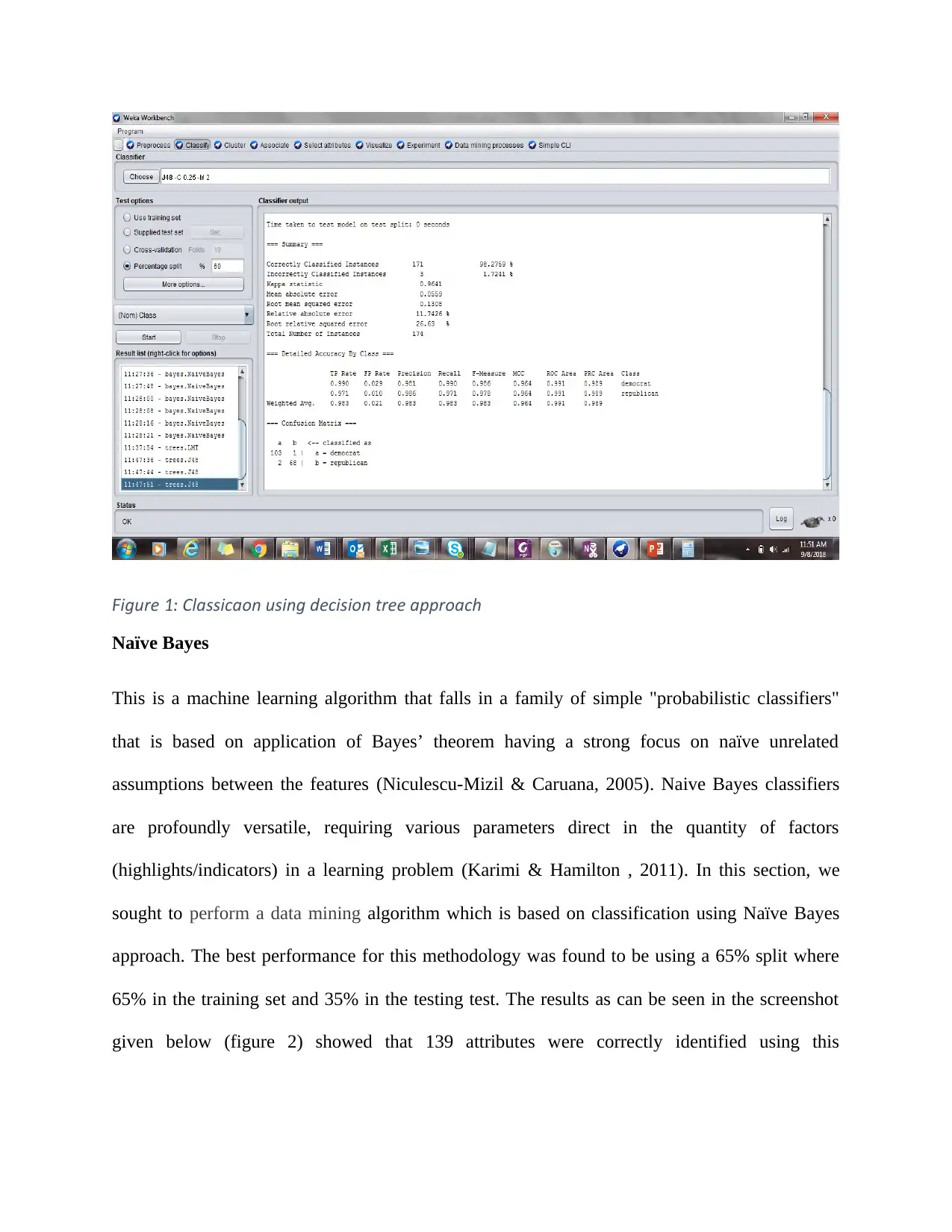
igureF 1 Classification using decision tree approach:
Naïve Bayes
This is a machine learning algorithm that falls in a family of simple "probabilistic classifiers"
that is based on application of Bayes’ theorem having a strong focus on naïve unrelated
assumptions between the features (Niculescu-Mizil & Caruana, 2005). Naive Bayes classifiers
are profoundly versatile, requiring various parameters direct in the quantity of factors
(highlights/indicators) in a learning problem (Karimi & Hamilton , 2011). In this section, we
sought to perform a data mining algorithm which is based on classification using Naïve Bayes
approach. The best performance for this methodology was found to be using a 65% split where
65% in the training set and 35% in the testing test. The results as can be seen in the screenshot
given below (figure 2) showed that 139 attributes were correctly identified using this

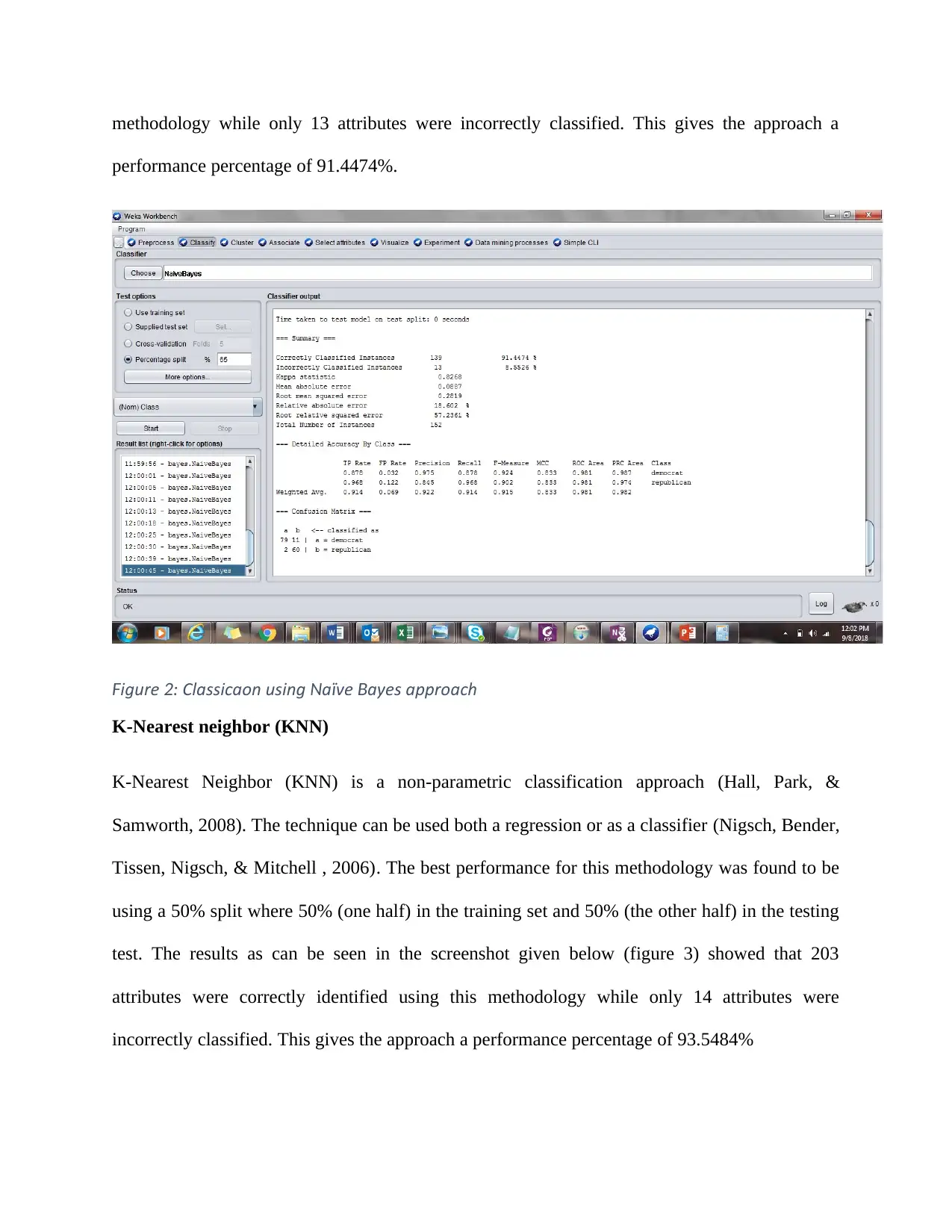
methodology while only 13 attributes were incorrectly classified. This gives the approach a
performance percentage of 91.4474%.
igureF 2 Classification using a ve ayes approach: N ï B
K-Nearest neighbor (KNN)
K-Nearest Neighbor (KNN) is a non-parametric classification approach (Hall, Park, &
Samworth, 2008). The technique can be used both a regression or as a classifier (Nigsch, Bender,
Tissen, Nigsch, & Mitchell , 2006). The best performance for this methodology was found to be
using a 50% split where 50% (one half) in the training set and 50% (the other half) in the testing
test. The results as can be seen in the screenshot given below (figure 3) showed that 203
attributes were correctly identified using this methodology while only 14 attributes were
incorrectly classified. This gives the approach a performance percentage of 93.5484%

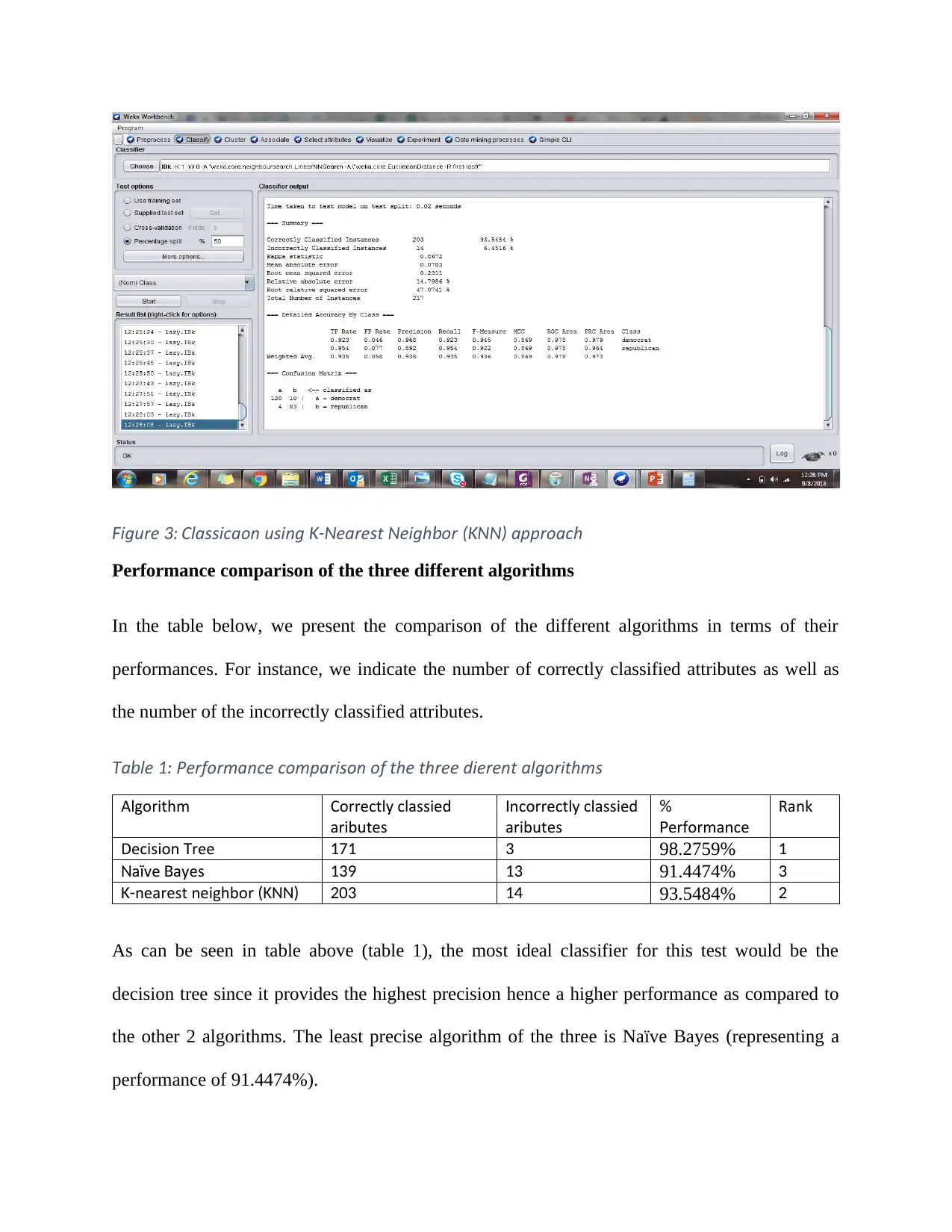
igureF 3: Classification using earest eigh or approachK-N N b (KNN)
Performance comparison of the three different algorithms
In the table below, we present the comparison of the different algorithms in terms of their
performances. For instance, we indicate the number of correctly classified attributes as well as
the number of the incorrectly classified attributes.
a leT b 1 Performance comparison of the three different algorithms:
Algorithm Correctly classified
attributes
ncorrectly classifiedI
attributes
%
erformanceP
Rank
Decision reeT 171 3 98.2759% 1
a ve ayesN ï B 139 13 91.4474% 3
nearest neighborK- (KNN) 203 14 93.5484% 2
As can be seen in table above (table 1), the most ideal classifier for this test would be the
decision tree since it provides the highest precision hence a higher performance as compared to
the other 2 algorithms. The least precise algorithm of the three is Naïve Bayes (representing a
performance of 91.4474%).

References
Hall, P., Park, B. U., & Samworth, R. J. (2008). Choice of neighbor order in nearest-neighbor
classification. Annals of Statistics, 36(5), 2135–2152. doi:10.1214/07-AOS537
Kamiński, B., Jakubczyk, M., & Szufel, P. (2017). A framework for sensitivity analysis of
decision trees. Central European Journal of Operations Research, 14(6), 111-123.
doi:10.1007/s10100-017-0479-6
Karimi, K., & Hamilton , H. J. (2011). Generation and Interpretation of Temporal Decision
Rules. International Journal of Computer Information Systems and Industrial
Management Applications, 3(2),12-19.
Niculescu-Mizil, A., & Caruana, R. (2005). Predicting good probabilities with supervised
learning. British Journal of the Philosophy of Science, 9(5), 45-54.
doi:10.1145/1102351.1102430
Nigsch, F., Bender, A., Tissen, J., Nigsch, E., & Mitchell , J. B. (2006). Melting point prediction
employing k-nearest neighbor algorithms and genetic parameter optimization. Journal of
Chemical Information and Modeling, 46(6), 2412–2422.