Data Mining and Visualization Assessment Item 2: PCA and Naive Bayes

This document presents a comprehensive analysis of a data mining assignment focusing on two key techniques: Principal Component Analysis (PCA) and Naive Bayes classification. The PCA section details dimension reduction using XLMiner in Excel, identifying key variables from the reduced principal component matrix and discussing the need for data normalization based on variance. The advantages and disadvantages of employing PCA are also outlined. The Naive Bayes section involves training data extraction, partition, and pivot table creation to calculate the probability of customers taking a loan offer based on their credit card ownership and online service usage. The analysis culminates in the calculation of the Naive Bayes probability, demonstrating how customer profiles influence loan application likelihood.

Data Mining and Visualization
Assessment Item – 2
[Pick the date]
Student name and id

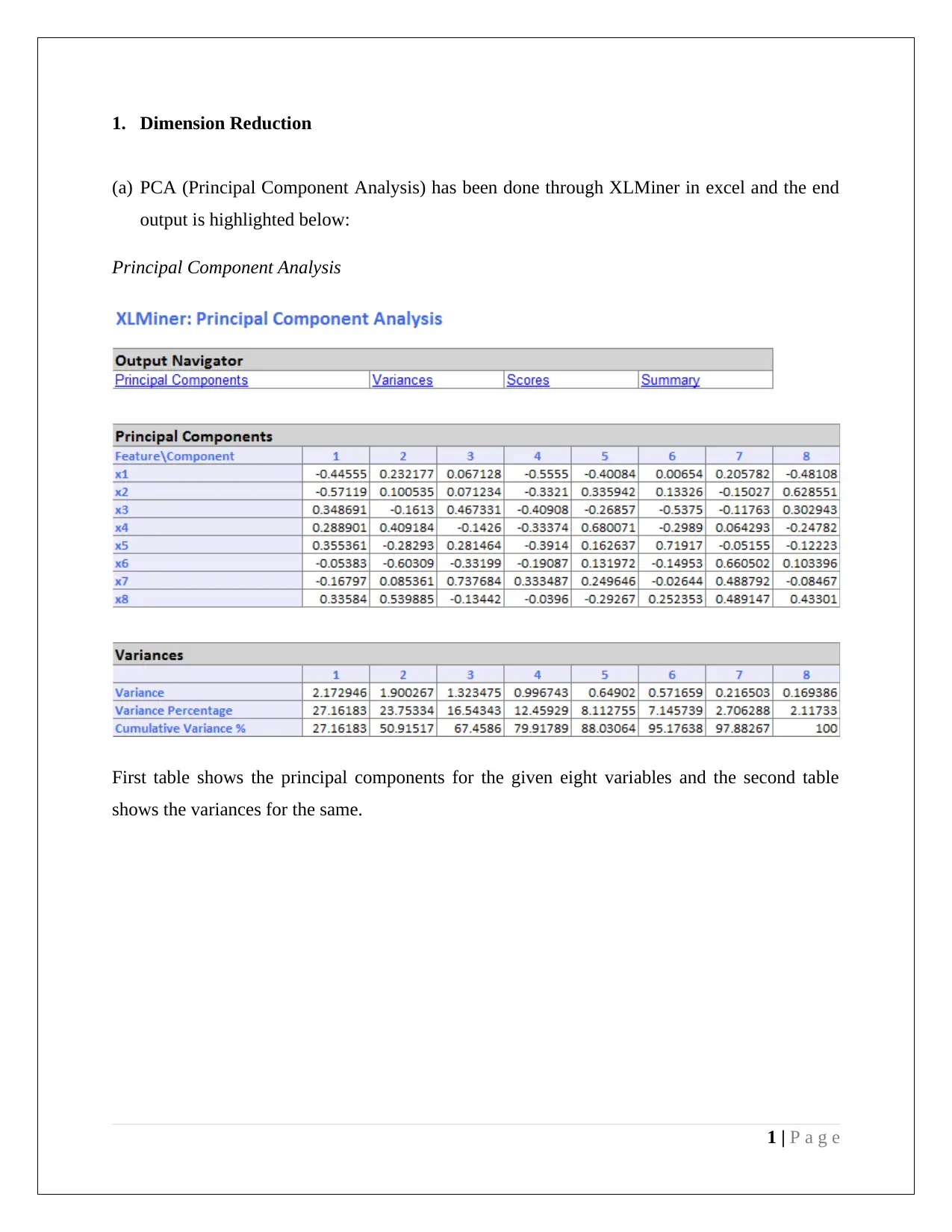
1. Dimension Reduction
(a) PCA (Principal Component Analysis) has been done through XLMiner in excel and the end
output is highlighted below:
Principal Component Analysis
First table shows the principal components for the given eight variables and the second table
shows the variances for the same.
1 | P a g e

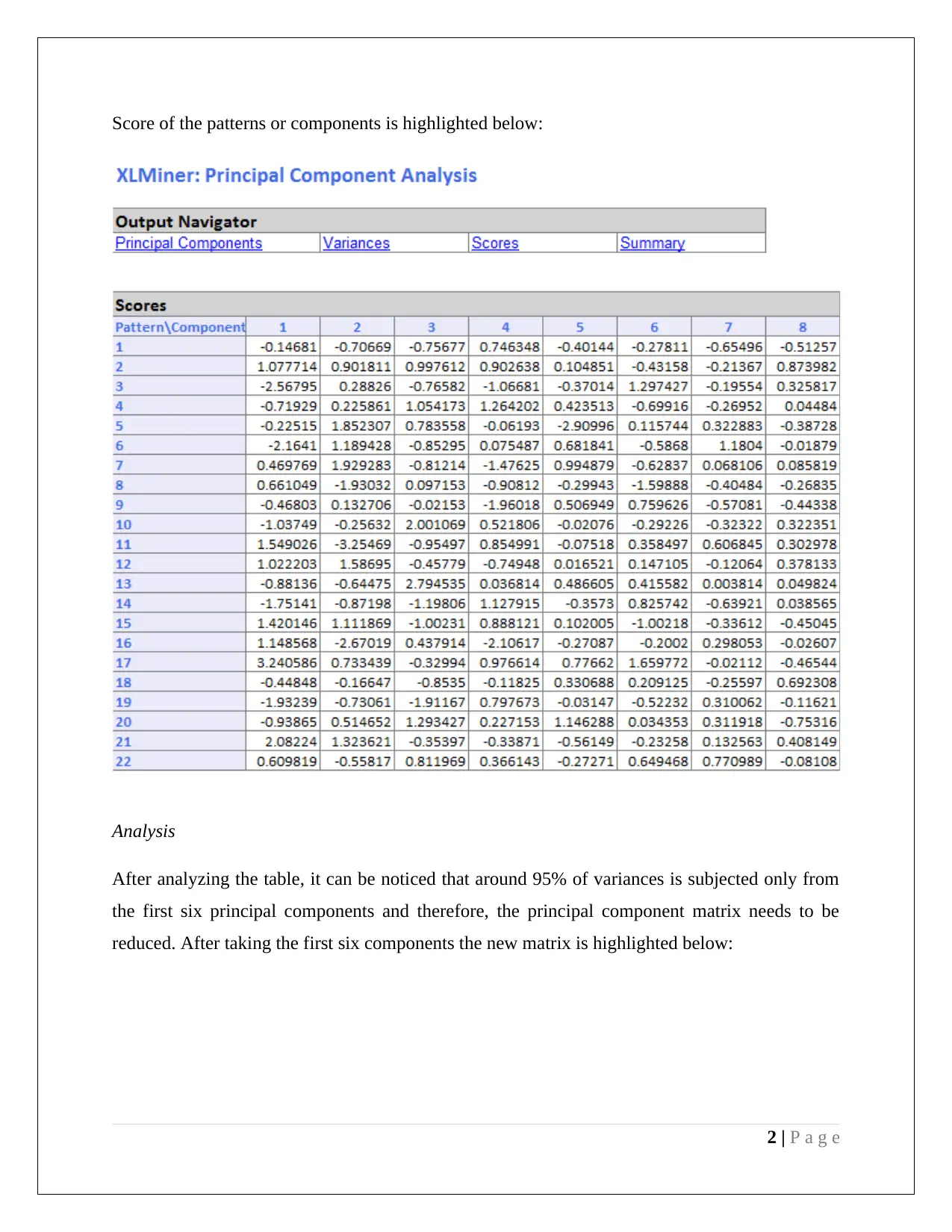
Score of the patterns or components is highlighted below:
Analysis
After analyzing the table, it can be noticed that around 95% of variances is subjected only from
the first six principal components and therefore, the principal component matrix needs to be
reduced. After taking the first six components the new matrix is highlighted below:
2 | P a g e

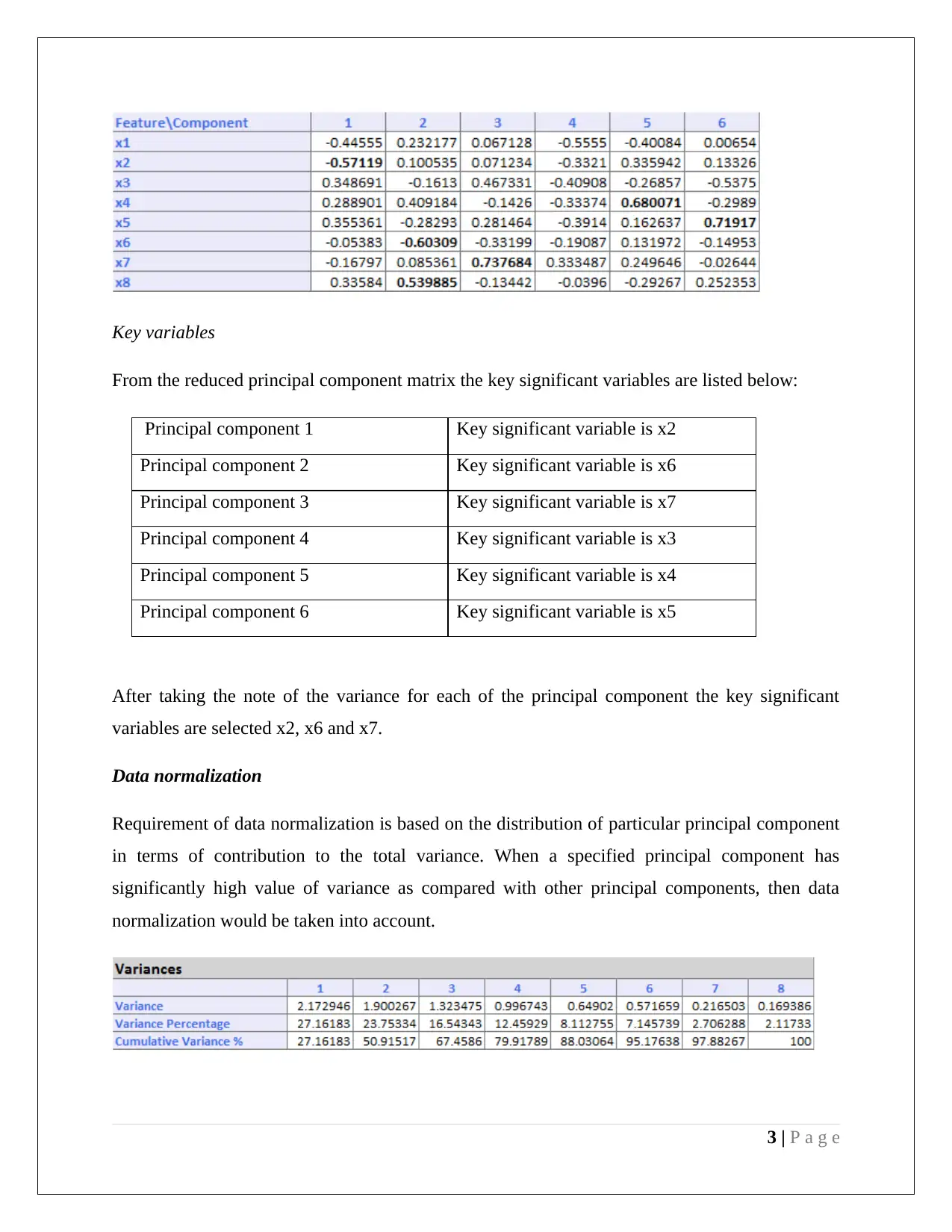
Key variables
From the reduced principal component matrix the key significant variables are listed below:
Principal component 1 Key significant variable is x2
Principal component 2 Key significant variable is x6
Principal component 3 Key significant variable is x7
Principal component 4 Key significant variable is x3
Principal component 5 Key significant variable is x4
Principal component 6 Key significant variable is x5
After taking the note of the variance for each of the principal component the key significant
variables are selected x2, x6 and x7.
Data normalization
Requirement of data normalization is based on the distribution of particular principal component
in terms of contribution to the total variance. When a specified principal component has
significantly high value of variance as compared with other principal components, then data
normalization would be taken into account.
3 | P a g e

The variances table shows that the highest percentage of variance is 27.16% which is for
principal component 1, which is not very high. Hence, it would be fair to cite that the other
principal components also having subsequent weightage of variance in total variance. Therefore,
data normalization is not mandatory for the provided data.
(b) Advantages and disadvantages of PCA
Advantages of employing PCA technique over other techniques are outlined below:
 This technique uses the free cloud of pointing the components in m- dimensional space and
hence, several attributes can be visualized in a simpler way.
 The level of degree of extent of the mean for the variables can easily be determined.
 This reduces the sizable data set into simpler set of data without changing the originality of
data set.
 Multiple dimensions would easily be reduced to lower number of dimensions for high
number of variable ranges.
 This uses orthogonal matrix to represent the result, which is relatively easy to analyze.
Disadvantages of employing PCA technique over other techniques are outlined below:
 Suitable only for the variables which have linear relations and orthogonal projections.
Therefore, it cannot be used when there is a nonlinear relationship which exists among the
variables.
 It cannot be used to analyze data when it is taken from a blind source separation because of
the underlying approach used in PCA which is not suitable here.
 It is quite difficult to determine the highest variance principal component when the
difference in variance is very minimal.
4 | P a g e

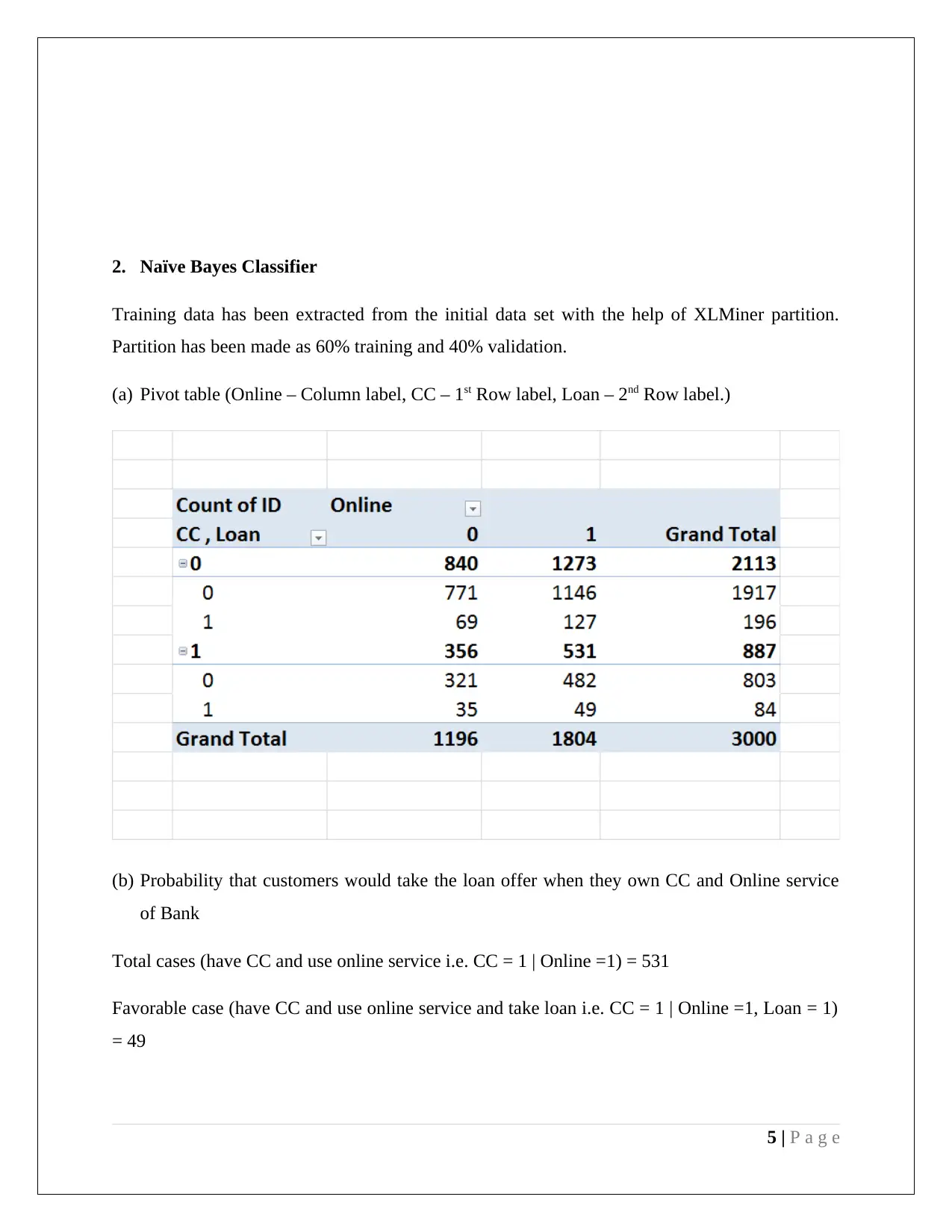
2. Naïve Bayes Classifier
Training data has been extracted from the initial data set with the help of XLMiner partition.
Partition has been made as 60% training and 40% validation.
(a) Pivot table (Online – Column label, CC – 1st Row label, Loan – 2nd Row label.)
(b) Probability that customers would take the loan offer when they own CC and Online service
of Bank
Total cases (have CC and use online service i.e. CC = 1 | Online =1) = 531
Favorable case (have CC and use online service and take loan i.e. CC = 1 | Online =1, Loan = 1)
= 49
5 | P a g e

Probability ¿ 49
531=0.092
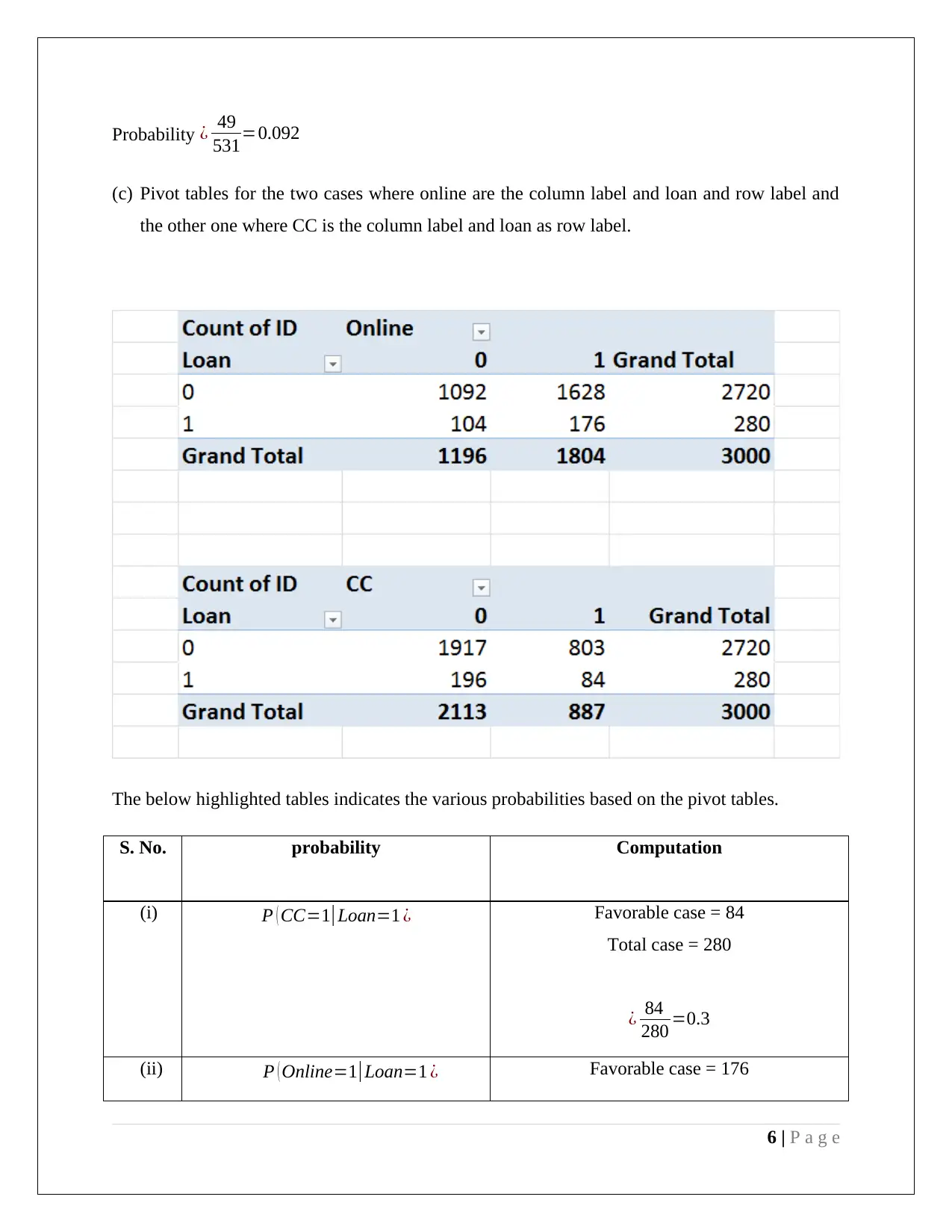
(c) Pivot tables for the two cases where online are the column label and loan and row label and
the other one where CC is the column label and loan as row label.
The below highlighted tables indicates the various probabilities based on the pivot tables.
S. No. probability Computation
(i) P ( CC=1| Loan=1 ¿ Favorable case = 84
Total case = 280
¿ 84
280 =0.3
(ii) P ( Online=1|Loan=1 ¿ Favorable case = 176
6 | P a g e

Total case = 280
¿ 176
280 =0.628
(iii) P ( Loan=1 ) Favorable case = 280
Total case = 3000
¿ 280
3000 =0.093
(iv) P ( CC=1|Loan=0¿ Favorable case = 803
Total case = 2720
¿ 803
2720 =0.295
(v) P ( Online=1|Loan=0 ¿ Favorable case = 1628
Total case = 2720
¿ 1628
2720 =0.598
(vi) P ( Loan=0 ) Favorable case = 2720
Total case = 3000
¿ 2720
3000 =0.906
(d) The Naïve Bayes Probability would be calculated based on the result obtained in part ©.
P ( Loan=1|CC =1, Online=1 ) = ( 0.3∗0.628∗0.093 )
( 0.3∗0.628∗0.093 ) + ( 0.295∗0.598∗0.906 )
P ( Loan=1|CC =1, Online=1 ) = 0.01752
0.01752+0.1598 =0.0987
7 | P a g e