Electrical Engineering Assignment: Data Representation and Logic

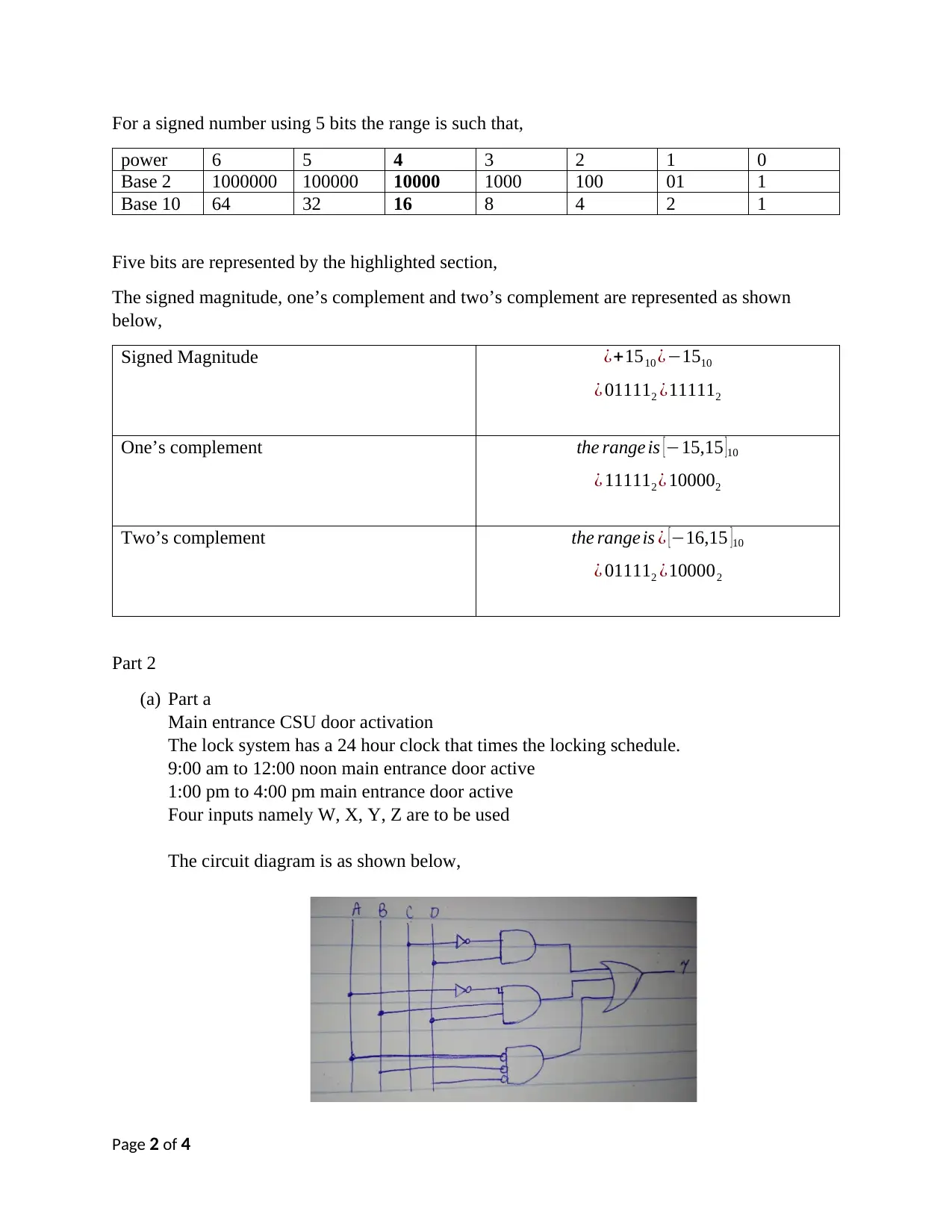
This document presents a comprehensive solution to a data representation and digital logic assignment. The solution includes an explanation of number conversions, specifically focusing on IEEE-754 representation and signed number systems using 5 bits. It covers signed magnitude, one's complement, and two's complement representations. The assignment also addresses a practical circuit design problem involving a main entrance door activation system with a 24-hour clock and four inputs. A truth table and Karnaugh map are used to derive a Boolean expression for the circuit. The solution further demonstrates the simplification of a Boolean expression using Boolean algebra identities, providing detailed steps and justifications for each simplification. The assignment covers several key concepts within digital logic and data representation, making it a valuable resource for students studying electrical engineering or related fields.

Student name
Subject code
Lecturer
Date of submission
Data Representation and Digital Logic
Part 1
(a) Number conversions
It is important to note that there are two kinds of zeros: +0 and -0
The value of an IEEE-754 number is computed as shown,
sign∗2exponent∗mantissa
The sign is stored in bit 32. The exponent can be computed from bits 24 to 31 by subtracting
the exponent obtained from 127. The mantissa is also referred to as the significand or
fraction. The significand is stored in bits of 1-23.
There is an invisible leading bit that is not stored in the memory but is placed as the first bit,
Therefore, in the given number
0 01111110 10100000000000000000000
0− positive signed number
01111110=12610
e xponent=12610−12710=−110
¿ (−1 )0∗( 1+ 0.625 )∗2−1
¿ 1.625∗1
2
¿ 0.812510
(b) Equivalents of “word” using 5 bits
(i) Signed number
(ii) One’s complement
(iii) Two’s complement
Page 1 of 4

For a signed number using 5 bits the range is such that,
power 6 5 4 3 2 1 0
Base 2 1000000 100000 10000 1000 100 01 1
Base 10 64 32 16 8 4 2 1
Five bits are represented by the highlighted section,
The signed magnitude, one’s complement and two’s complement are represented as shown
below,
Signed Magnitude ¿+1510 ¿−1510
¿ 011112 ¿111112
One’s complement the range is [−15,15 ]10
¿ 111112 ¿ 100002
Two’s complement the range is ¿ [−16,15 ]10
¿ 011112 ¿100002
Part 2
(a) Part a
Main entrance CSU door activation
The lock system has a 24 hour clock that times the locking schedule.
9:00 am to 12:00 noon main entrance door active
1:00 pm to 4:00 pm main entrance door active
Four inputs namely W, X, Y, Z are to be used
The circuit diagram is as shown below,
Page 2 of 4

From the output, we can develop a Boolean expression using Karnaugh maps as shown
below,
Grouping the terms in the powers of 2 we obtain,
A' B' D'+ A' BD+C' D=Y
Page 3 of 4
Inputs Output
A B C D Q
0 0 0 0 1
0 0 0 1 1
0 0 1 0 1
0 0 1 1 0
0 1 0 0 0
0 1 0 1 1
0 1 1 0 0
0 1 1 1 1
1 0 0 0 0
1 0 0 1 1
1 0 1 0 0
1 0 1 1 0
1 1 0 0 0
1 1 0 1 1
1 1 1 0 0
1 1 1 1 0

(b) Using basic Boolean algebra identical ties for Boolean Variables A, B and C, prove that
X’Y + XYZ’ + Y’ + XZ (Y+Y’) = 1. Please show all steps and mention the identities
used. [6 marks]
There are several basic laws that govern the Boolean Algebra computations. These laws
enable a complex system to be simplified to the least number.
Assuming that the Boolean Variables A, B, C are X, Y, Z respectively.
X’Y + XYZ’ + Y’ + XZ (Y+Y’) = 1
Solution
A' B+ AB C' + B'+ AC
Simplifying further, making B a common factor in both terms,
B ( A' + A C' ) + B' + AC
Simplifying by introducing C in the brackets,
B ( A' C + A' C'+ A C' ) + B'+ AC
The first and last term in brackets demonstrate an Exclusive-Or condition of the equation,
A' C+ A C'=A ⊕C … .. exclusive∨¿
B ( A' C' ( A ⊕C )+ AC )+ ABC + B'
A' C ' ( A ⊕C ) =0
B' + AC
From the identities,
Assuming the A, C represents high and B’ represents low,
B'+ AC=1
Page 4 of 4