ITC544 Assignment 1: In-Depth Analysis of Data Representation & Logic

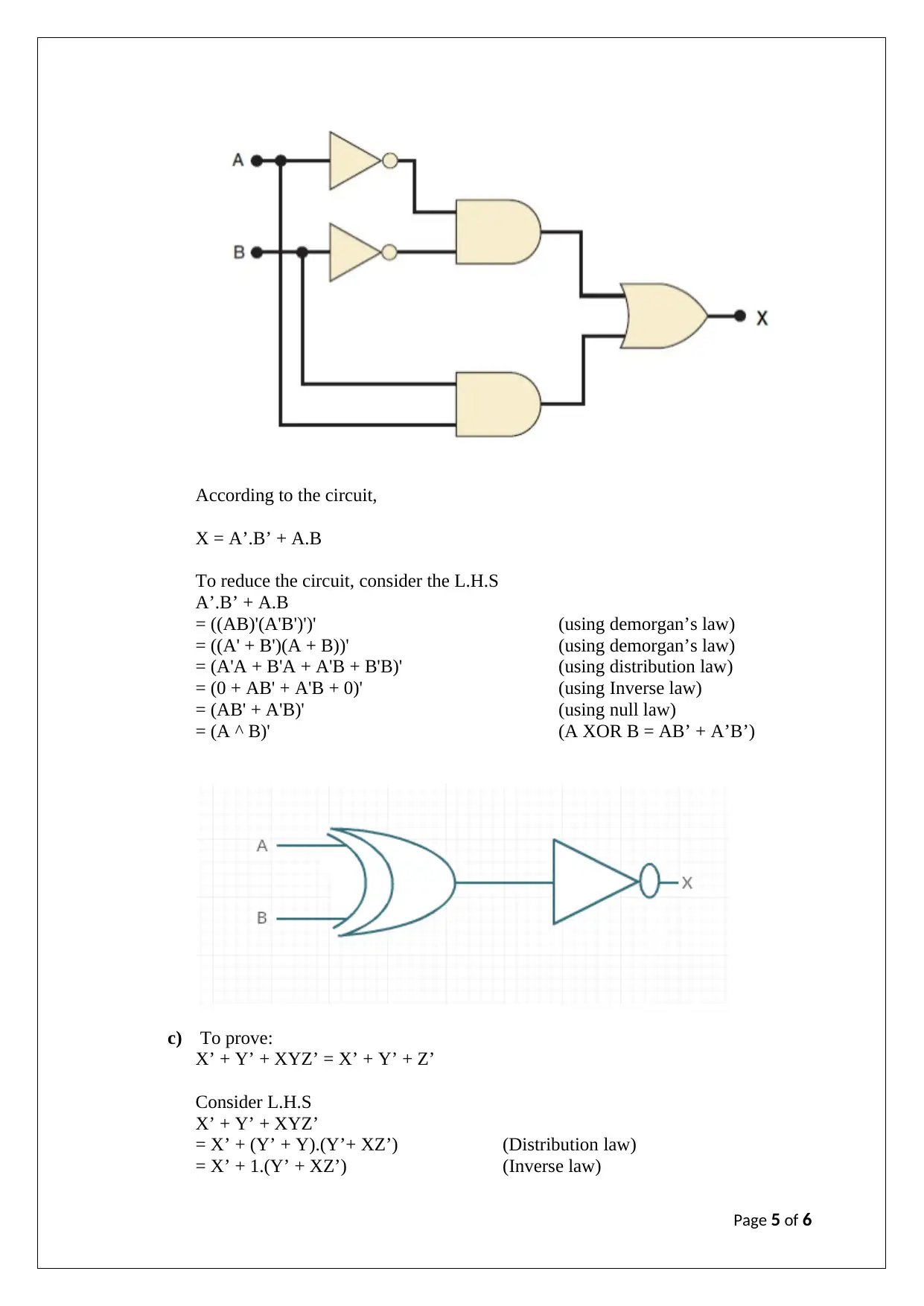
This ITC544 assignment solution delves into data representation and digital logic, addressing questions related to number system conversions and circuit simplification. The assignment begins by determining the base 'x' for a given equation involving hexadecimal and base 'x' numbers. It proceeds to convert numbers between different bases, including hexadecimal to base-3, base-7 to binary, base-5 to octal, and base-8 to decimal. Further, the document explores the representation of numbers in one's complement, two's complement, and signed magnitude formats, identifying the lowest negative and highest positive values for a 3-bit computer. The assignment also examines the equivalence of two combinational circuits using Boolean algebra and truth tables. Lastly, the document includes a question on circuit reduction using Boolean identities and laws, along with a proof involving DeMorgan's law, distribution law, and inverse law. Desklib provides a platform for students to access similar solved assignments and past papers.

Page 1 of 6
[WRITE YOUR FULL NAME]
[WRITE YOUR STUDENT ID]
ITC544
ASSIGNMENT 1: DATA REPRESENTATION AND DIGITAL LOGIC)

Question 1
a) (152)x = (6A)16
x = ?
6A is in hexadecimal, the decimal representation will be
6 * 161 + 10 * 160
= 96 + 10
= 106 in decimal
152 is with base x, the decimal representation will be
1 * x2 + 5 * x1 + 2 * x0
x2 + 5x + 2 in decimal
Therefore, x2 + 5x + 2 = 106
x2 + 5x – 104 = 0
x2 + 13x – 8x – 104 = 0
(x + 13)(x – 8) = 0
x = 8, x = -13
As the value of base cannot be negative.
Therefore x = 8.
b)
i) 0xBED into 3-base representation
BED is in hexadecimal, the decimal representation is:
11 * 162 + 14 * 161 + 13 * 160
= 2816 + 224 + 13
= 3053
Now, 3053 is converted to base 3
3 3053 2
3 1017 0
3 339 0
3 113 2
3 37 1
3 12 0
3 4 1
3 1 1
0
Page 2 of 6
[WRITE YOUR FULL NAME]
[WRITE YOUR STUDENT ID]
ITC544
ASSIGNMENT 1: DATA REPRESENTATION AND DIGITAL LOGIC)

Now, these remainders are written upside down, therefore,
0xBED = (11012002)3
ii) (321)7 into 2-base (binary) representation
321 is in base 7, the decimal representation is:
3 * 72 + 2 * 71 + 1 * 70
= 147 + 14 + 1
= 162
Now, 162 is converted to binary
2 162 0
2 81 1
2 40 0
2 20 0
2 10 0
2 5 1
2 2 0
2 1 1
0
Now, these remainders are written upside, therefore,
(321)7 = (10100010)2
iii) (123)5 into octal representation
123 is in base 5, the decimal representation is:
1 * 52 + 2 * 51 + 3 * 50
= 25 + 10 + 3
= 38
Now, 38 is converted to base 8
8 38 6
8 4 4
0
Now, these remainders are written upside down, therefore,
(123)5 = (46)8
iv) (21.21)8 into decimal representation
2 * 81 + 1 * 80 + 2 * 8-1 + 1 * 8-2
= 16 +1+ 0.25+0.015625
= (17.265625)10
c)
i) One’s complement
Lowest value (negative)  011
Page 3 of 6

Highest value (positive)  111
ii) Two’s complement
Lowest value (negative)  100
Highest value (positive)  011
iii) Signed Magnitude
Lowest value (negative)  – 3
Highest value (positive)  + 3
Question 2
a)
In circuit 1,
X1 = (A.B)’
In circuit 2,
X2 = A’ + B’
Considering, R.H.S for circuit 1
(A.B)’
= A’ + B’ (using Demorgan’s law (X.Y)’ = X’ + Y’)
= X2 (Boolean function of circuit 2)
Therefore, both the circuits are equal.
Using truth table,
A B A.
B
X1 A’ B’ X2
0 0 0 1 1 1 1
0 1 0 1 1 0 1
1 0 0 1 0 1 1
1 1 1 0 0 0 0
As the columns of X1 and X2 are equal, therefore, both the circuits are equal.
b)
Page 4 of 6

According to the circuit,
X = A’.B’ + A.B
To reduce the circuit, consider the L.H.S
A’.B’ + A.B
= ((AB)'(A'B')')' (using demorgan’s law)
= ((A' + B')(A + B))' (using demorgan’s law)
= (A'A + B'A + A'B + B'B)' (using distribution law)
= (0 + AB' + A'B + 0)' (using Inverse law)
= (AB' + A'B)' (using null law)
= (A ^ B)' (A XOR B = AB’ + A’B’)
c) To prove:
X’ + Y’ + XYZ’ = X’ + Y’ + Z’
Consider L.H.S
X’ + Y’ + XYZ’
= X’ + (Y’ + Y).(Y’+ XZ’) (Distribution law)
= X’ + 1.(Y’ + XZ’) (Inverse law)
Page 5 of 6

= X’ + Y’ + XZ’ (Identity law)
= (X’ + X).(X’ + Z’) + Y’ (Distribution law)
= 1.(X’ + Z’) + Y’ (Inverse law)
= X’ + Z’ + Y’ (Identity law)
= X’ + Y’ + Z’ (Commutative law)
= R.H.S
Hence, proved.
Page 6 of 6