Data Science Module: Comprehensive Graph Theory Assignment Solution
VerifiedAdded on 2023/01/17
|4
|681
|46
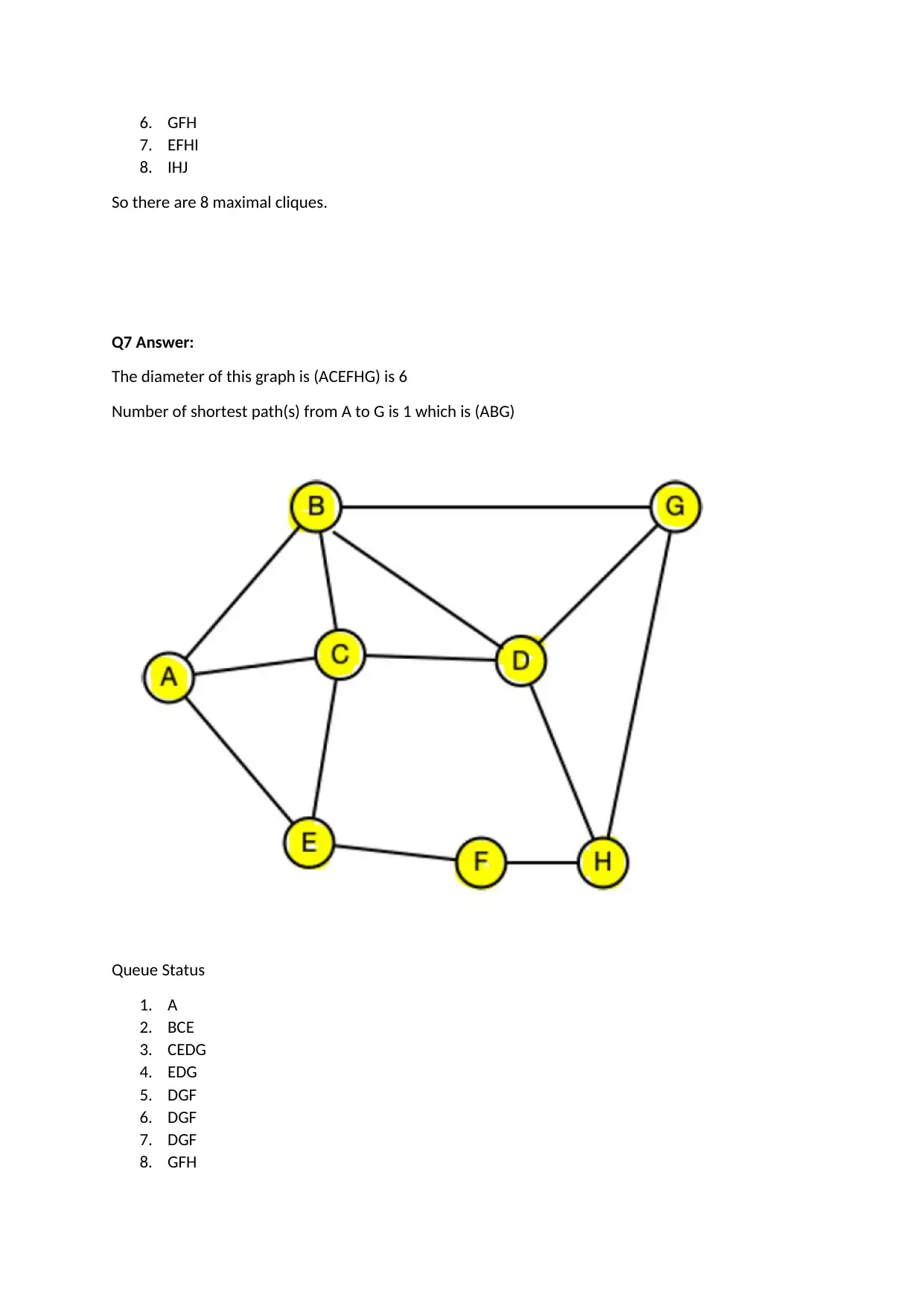
Homework Assignment
AI Summary
This assignment solution covers a range of graph theory concepts. It begins by identifying the shortest path in a graph and calculating its total weight. The solution then determines whether a given graph is strongly connected and proposes a modification to achieve strong connectivity. Further, it addresses graph isomorphism, providing mappings between nodes. Clustering coefficients are calculated for specific nodes, and the strong triadic closure property is analyzed. The solution also lists maximal cliques within a graph and determines its diameter. Finally, it analyzes shortest paths and flow amounts in a graph using breadth-first search.
1 out of 4






![[object Object]](/_next/static/media/star-bottom.7253800d.svg)