CP5602 Algorithm Analysis Assignment: Data Structures and Algorithms

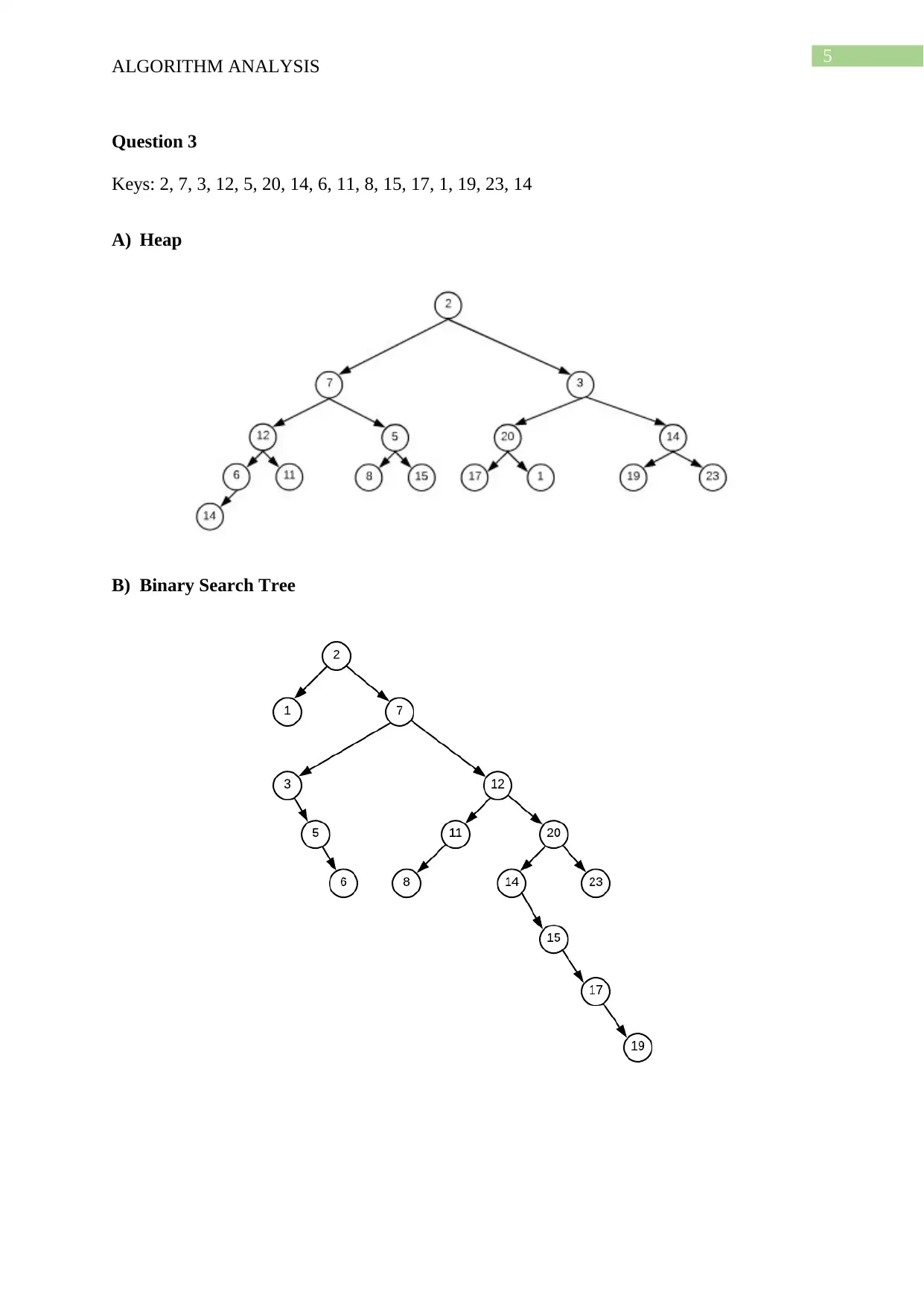
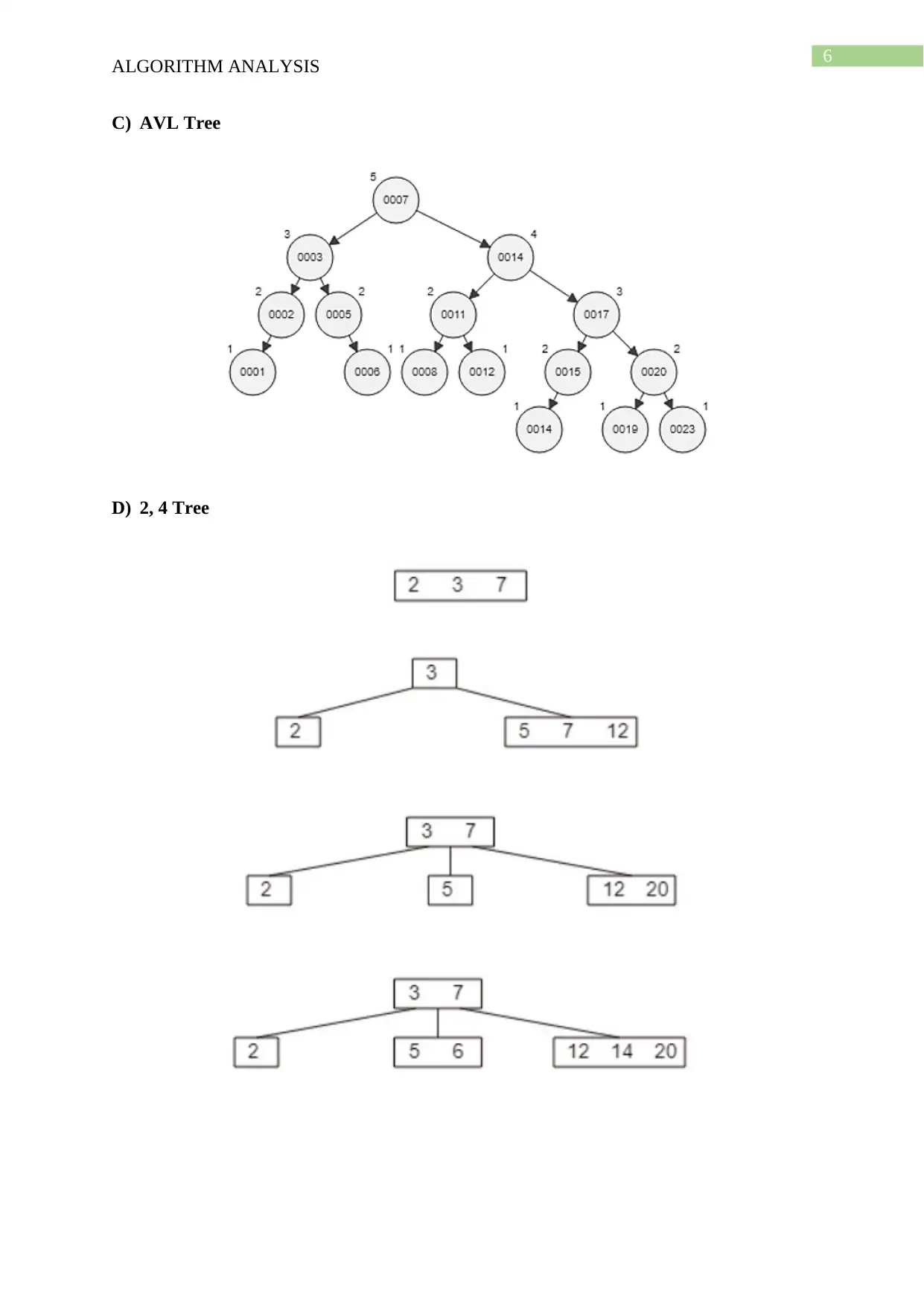
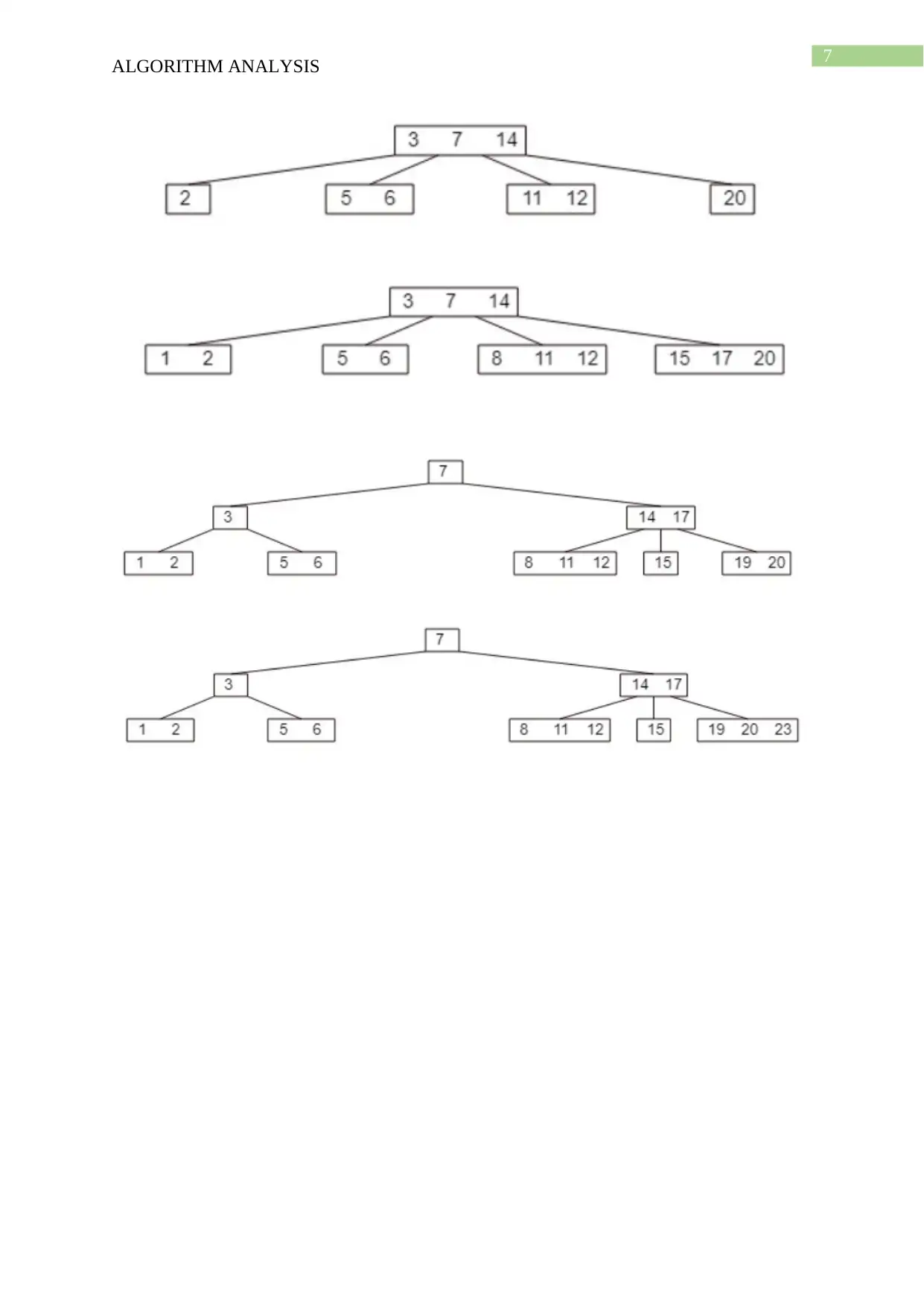
This document presents a comprehensive solution to an algorithm analysis assignment, covering various topics including iterative and recursive binary search algorithms with complexity analysis, different hashing techniques such as separate chaining, linear probing, quadratic probing, and secondary hashing, along with their implementations. It also delves into data structures like heaps, binary search trees, AVL trees, and 2-4 trees, illustrating their construction with a given set of keys. Furthermore, the solution includes finding the Longest Common Subsequence (LCS) of two arrays and determining the optimal matrix chain order using dynamic programming. Lastly, it analyzes string searching algorithms like brute-force, Boyer-Moore, and Knuth-Morris-Pratt, and determines if a given graph is strongly connected using transitive closure. Desklib offers a wide range of solved assignments and study materials to support students in their academic endeavors.

Running head: ALGORITHM ANALYSIS
Algorithm Analysis
Name of the Student:
Name of the University:
Author note:

1
ALGORITHM ANALYSIS
Question 1
a) Iterative Binary Search
BinarySearch(A[1..n], v)
//considering the array is sorted in increasing order
low = 0
high = n - 1
while low <= high
mid = (low + high) / 2
if A[mid] > v
high = mid - 1
else if A[mid] < v
low = mid + 1
else
return mid
return v_not_found
Complexity: O(log n)
b) Iterative Binary Search
BinarySearch(A[1..n], v, low, high)
//considering the array is sorted in increasing order
if high < low
return v_not_found
mid = (low + high) / 2
if A[mid] > v
return BinarySearch(A[], v, low, mid-1) //recursive call with first half of array
else if A[mid] < v
return BinarySearch(A[], v, mid+1, high) //recursive call with last half of array
else

2
ALGORITHM ANALYSIS
return mid
Complexity: O(log n)
For Binary Search, T(N) = T(N/2) + O(1) This is the recurrence relation.
Applying Masters Theorem to compute Run time complexity of recurrence relation:
T(N) = aT(N/b) + f(N)
Now,
a = 1 and b = 2
=> log (a base b) = 1
f(N) = n^c log^k(n) //k = 0 & c = log (a base b)
So, T(N) = O(N^c log^(k+1)N)
= O(log(N))

3
ALGORITHM ANALYSIS
Question 2
a) Separate Chaining
Hash function h(i) = (3i + 5) mod 13
Set of keys= 14, 42, 15, 81, 27, 92, 3, 39, 20, 16, and 5
0 1 2 3 4 5 6 7 8 9 10 11 12
20 42 39 5 14 15
81 27
3 92
16
b) Linear Probing
Hash function h(i) = (3i + 5) mod 13
Set of keys= 14, 42, 15, 81, 27, 92, 3, 39, 20, 16, and 5
0 1 2 3 4 5 6 7 8 9 10 11 12
20 42 81 3 16 39 5 14 27 92 15
c) Quadratic Probing
Hash function h(i) = (3i + 5) mod 13
Set of keys= 14, 42, 15, 81, 27, 92, 3, 39, 20, 16, and 5
0 1 2 3 4 5 6 7 8 9 10 11 12
20 42 92 5 16 39 27 81 14 3 15

4
ALGORITHM ANALYSIS
d) Secondary Hashing
Hash function h(i) = (3i + 5) mod 13
Hash function h’(i) = 11 − (i mod 11)
Set of keys= 14, 42, 15, 81, 27, 92, 3, 39, 20, 16, and 5
0 1 2 3 4 5 6 7 8 9 10 11 12
42 27 81 14 15
Method failed with the attempt to insert 92.

5
ALGORITHM ANALYSIS
Question 3
Keys: 2, 7, 3, 12, 5, 20, 14, 6, 11, 8, 15, 17, 1, 19, 23, 14
A) Heap
B) Binary Search Tree

6
ALGORITHM ANALYSIS
C) AVL Tree
D) 2, 4 Tree

7
ALGORITHM ANALYSIS

8
ALGORITHM ANALYSIS
Question 4
A = (1, 1, 1, 0, 0, 0, 1, 0, 1)
B = (0, 1, 0, 1, 0, 0, 1, 1)
LCS of A and B is (1, 0, 0, 0, 1, 1)

9
ALGORITHM ANALYSIS
Question 5
Using the given matrix-chain <7, 10, 5, 18, 20, 40, 10, 15>,
A1 7 × 10
A2 10 × 5
A3 5 × 18
A4 18 × 20
A5 20 × 40
A6 40 × 10
A7 10 × 15
p0=7, p1=10, p2=5, p3=18, p4=20, p5=40, p6=10, p7=15
m[i, j] = 0, if i = j,
m[i,j]= {min {m[i,k] + m[k+1, j] + pi –1pkpj}}, if i < j
m[1,1] = m[2,2] = m[3,3] = m[4,4] = m[5,5] = m[6,6] = m[7,7] = 0
m[1,2] = p0xp1xp2 = 7x10x5 = 350
m[2,3] = p1xp2xp3 = 10x5x18 = 900
m[3,4] = p2xp3xp4 = 5x18x20 = 1800
m[4,5] = p3xp4xp5 = 18x20x40 = 14400
m[5,6] = p4xp5xp6 = 20x40x10 = 8000
m[6,7] = p4xp5xp6 = 40x10x15 = 6000
m 1 2 3 4 5 6 7
1 0 350
2 0 900
3 0 1800
4 0 14400
5 0 8000
6 0 6000
7 0

10
ALGORITHM ANALYSIS
Question 7
A) Brute-force algorithm
0 1 2 3 4 5 6 7 8 9 1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
2
1
2
2
2
3
b e l l i s a l a b e l a b e l b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
Found pattern at index: 16

11
ALGORITHM ANALYSIS
B) Boyer-Moore Algorithm
Indexes:
B 0
E 1
L 2
A 3
B 4
E 5
L 6
A 7
Length= 8
Formula for BAD-MATCH TABLE values = length-index-1
Letter b e l a *
Value 3 2 1 8 8
b e l l i s a l a b e l a b e l b e l a b e l a
b e l a b e l a
b e l a b e l a
b e l a b e l a
Match Found