Decision Modeling with Spreadsheets - Finance Assignment Report

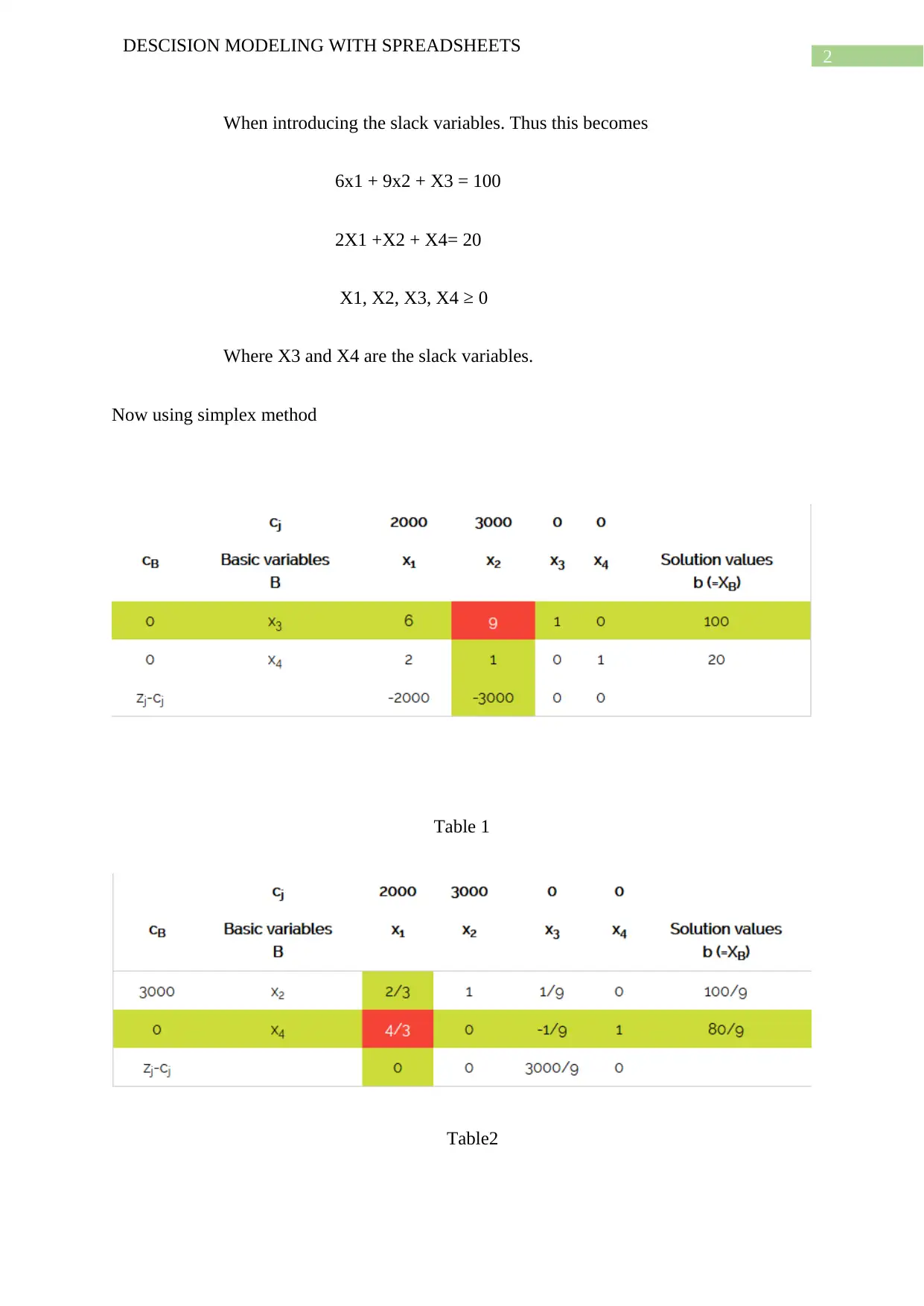
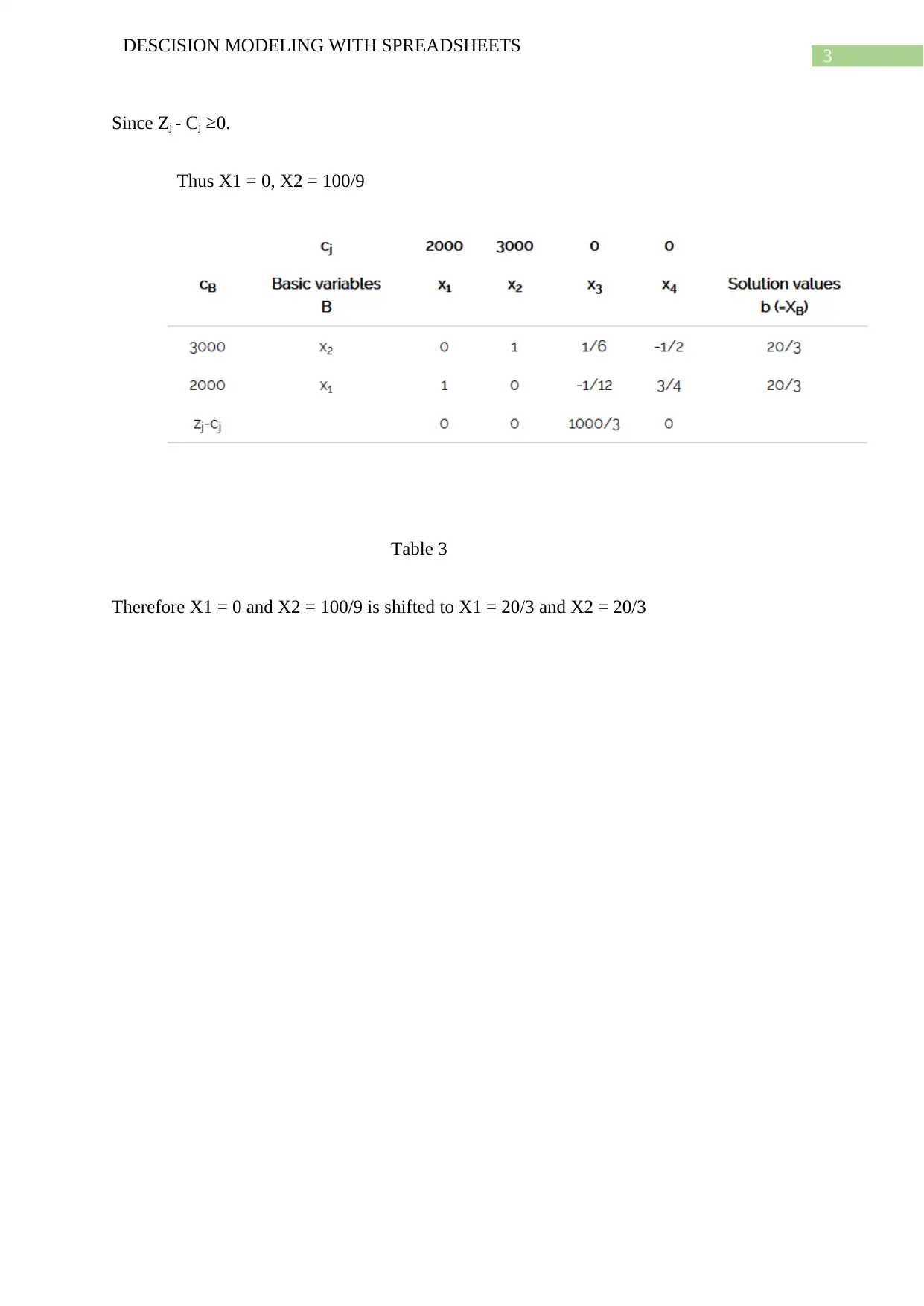
This report focuses on decision modeling using spreadsheets, particularly in the context of finance. It explores the concept of optimal solutions within the framework of linear programming problems (LPPs), emphasizing how to maximize or minimize objective functions while adhering to constraints. The report details the simplex method, a key technique for solving LPPs, and demonstrates how to identify multiple optimal solutions. It includes an example problem with slack variables and provides a step-by-step approach to solving the problem using the simplex method, along with the final optimal solution. The report also includes a bibliography with relevant references.

Running head: DESCISION MODELING WITH SPREADSHEETS
Decision Modelling with Spreadsheets
Name of the Student:
Name of the University:
Author Note:

1
DESCISION MODELING WITH SPREADSHEETS
Yes, a linear programming problem (LPP) have more than one optimal solution.
An optimal solution is a solution of feasible type, in which the objective function gain
their maximum or minimum value. In other words it is a solution, which either minimise or
maximise the objective function. Moreover it is also a solution of linear programming
problem which satisfies the constraints and also it gets the value of the objective function.
This kind of solution has been seen, when there are more than one basic solution of the linear
programming problem. Thus this maximize or minimize the objective function. In general the
optimal solution may not unique, when the non-basic variables have the zero coefficient in
the row of index. In other words the index row (Zj - Cj)
There are different methods to solve multiple optimal solution, like simplex method,
graphic method and so on. In this type of solution bringing the variable which is non basic,
which increase or decrease the basic variable and in to the value of the objective function.
For example,
Maximize
2000X1 +3000X2
Subject to
6x1 + 9x2 ≤ 100
2X1 +X2 ≤ 20
Where
X1, X2 ≥ 0
Solution:

2
DESCISION MODELING WITH SPREADSHEETS
When introducing the slack variables. Thus this becomes
6x1 + 9x2 + X3 = 100
2X1 +X2 + X4= 20
X1, X2, X3, X4 ≥ 0
Where X3 and X4 are the slack variables.
Now using simplex method
Table 1
Table2

3
DESCISION MODELING WITH SPREADSHEETS
Since Zj - Cj ≥0.
Thus X1 = 0, X2 = 100/9
Table 3
Therefore X1 = 0 and X2 = 100/9 is shifted to X1 = 20/3 and X2 = 20/3

4
DESCISION MODELING WITH SPREADSHEETS
Bibliography
Sinsuphan, N., Leeton, U., & Kulworawanichpong, T. (2013). Optimal power flow solution
using improved harmony search method. Applied Soft Computing, 13(5), 2364-2374.
Zhang, L., Mahdavi, M., Jin, R., Yang, T., & Zhu, S. (2013, June). Recovering the optimal
solution by dual random projection. In Conference on Learning Theory (pp. 135-157).