G&B Consulting - Deliverable 07: Worksheet and Solution Analysis

This assignment solution addresses Deliverable 07, focusing on business development strategies for G&B Consulting. The first part analyzes customer satisfaction records, calculating probabilities to predict client satisfaction and assessing the likelihood of maintaining high customer satisfaction ratings. The second part delves into game theory, using payoff matrices to determine dominant strategies and Nash equilibrium points for a legal dispute scenario. The solution explores different coworker approaches, including mixed strategy algorithms and non-simultaneous game trees with backward induction, to identify optimal strategies for both the manufacturer and its competitor. The analysis covers various aspects of strategic decision-making, including the application of binomial distribution, and the identification of non-credible threats within the game theory framework, providing a comprehensive overview of business strategy and problem-solving techniques.

Running head: DELIVERABLE 07 1
Deliverable 07 – Worksheet and Solution
Student:
Professor:
Institution Affiliation:
Course:
Date:

DELIVERABLE 07 2
Deliverable 07 – Worksheet and Solution
Part 1
The first item you want to highlight is your customer satisfaction record. Over the past 18
months of employment you have worked with 25 clients, and according to the customer
satisfaction surveys all clients are asked to take after their contract is completed, 22 of
them rated you with the highest level of satisfaction. Use this information to find the best
predicted probability of having a new client give the highest level of satisfaction.
However, having a single satisfied customer is not enough. It is very important to G & B
Consulting that they maintain high ethical standards and continue to receive the highest
rating from the Better Business Bureau consistently. In order to maintain this rating, the
company must maintain at least 85% or higher of customers giving you high customer
satisfaction ratings. Internal projections predict that G&B Consulting will serve 60 clients
over the next year. If you become the project manager and use your prior record as an
indicator, find the probability that 85% or more of new clients will give the highest level
of customer satisfaction rating. Show all calculations and formulas used. If you use Excel
for your calculations include that along with your submission. Use this information to
make a convincing argument that you are a good choice for the position. NOTE (The
solution for this part has been transferred to the last section of this paper due to the
format of this template)
1
 Calculate the probability of getting a satisfied client based off of your
prior work history at G& B Consulting. Show all work.
 Explain how you found your solution.
2
 Using your prior work history, calculate the probability of getting at least
85% of clients giving you high customer satisfaction ratings.
 Explain how you found your solution.
3
 Interpret your results from slide 2 and use them to make an argument on
why you would be good for the position.
Part 2
The other item you wish to highlight comes from some work done for a local
manufacturer. They believed that a competitor was illegally using one of their patents in
their own manufacturing process and were considering litigation. This competitor's
product were directly cutting into the manufacturer's profit, so they wanted to prevent the
competitor's product from being made and recoup those lost profits. Of course, the
litigation process is long and costly, and the outcome is not guaranteed and would likely

DELIVERABLE 07 3
result in a countersuit brought by the competitor. Before continuing with costly legal
counsel, the manufacturer hired G&B Consulting to help them determine their best
strategy.
This was potentially a very lucrative contract, and a high profile one too since the
manufacturer is one of the biggest employers in the area. Therefore, several analysts at
G&B Consulting, including you, were asked to tackle the problem independently to help
ensure the best possible results. Before compiling a final report to give to the
manufacturer, the results were presented to the project lead:
The first solution brought up was given by one of your coworkers. Using the
manufacturer's projections of profits solely, he was able to create the following payoff
matrix where each entry is in millions of dollars annually:
This coworker concluded that the manufacturer should always do the opposite of the
competitor chooses making this a strictly competitive game.
4
 Using the payoff matrix shown above, determine if the manufacturer has a
dominant strategy. Show and explain all steps.
Solution
Using the payoff matrix, we can determine if the manufacturer has a dominant strategy
by fixing competitor’s choices as follows;
5
The preference points for the manufacturer do not change when the strategies for the
competitor change. As a result, the manufacturer has a dominant strategy which is to sue.
Competitor
Manufacturer Sue Don’t Sue
Sue (5, -5) (20, -20)
Don’t Sue (-15, 15) (-10, 10)
Competitor
Manufacturer Sue Don’t Sue
Sue (5, -5) (20, -20)
Don’t Sue (-15, 15) (-10, 10)
Competitor
Manufacturer Sue Don’t Sue
Sue (5, -5) (20, -20)
Don’t Sue (-15, 15) (-10, 10)

DELIVERABLE 07 4
When the manufacture decides to take a court proceeding, there will be some paybacks
and the competitor will suffer losses. Suing is a dominant strategy for the manufacturer
regardless of whether the competitor sues or does not sue.
 Using the payoff matrix shown above, determine if the competitor has a
dominant strategy. Show and explain all steps.
Solution
So as determine whether the competitor has a dominant strategy, we use the payoff
matrix and fix the manufacturer’s choices. From the above payoff matrix, it is clear that
the competitor does not have a dominant strategy.
4.
 Find all Nash equilibrium points. Show and explain all steps.
In this game, there is one Nash equilibrium points which is (Sue, Sue). At this point, no
one would wish to break the law even in the absence of the police (Xiang et al., 2018).
Precisely, at (Sue, Sue), if the competitor decides to avoid a court proceeding when the
manufacturer settles on suing, the competitor will definitely lose. On the other hand, if
the manufacturer decides on failing to sue when the competitor decides to sue, the
manufacturer will definitely lose. No one would want to lose in a game, thus (Sue, Sue) is
a Nash equilibrium point.
5. Identify the optimum strategy of the game.
Solution
Assume that the manufacturer believes that the competitor will play Sue with a
probability of p. On the other hand, assume that the competitor believes that the
manufacturer will play Sue with a probability of q.
To determine the projected payoff that makes each player indifferent between the two
strategies, we compute as follows;
For the manufacturer;
5p + 20(1-p) = 10p + 15(1-p)
5p + 20 – 20P = 10p + 15 -15p
20 -15P = 15 – 5p
5 = 10p
P = 0.5
For the competitor;
-5q + 20(1-q) = 10q + 15 (1-q)
-5q – 20q + 20 = 10q – 15q + 15
20 q = 5

DELIVERABLE 07 5
5/20 = q = 0.25
Thus, the combined optimal strategies for the game are (0.5, 0.5) and (0.25, 0.75).
6
 Do your results match those of your coworkers? Explain why you agree
or disagree
My results do not match with those of my competitors. I disagree with them on the point
that the manufacturer should always do the contrary of the competitor decides making
this a firmly competitive game. I disagree because in my calculations, I only realized one
Nash equilibrium point that is (Sue, Sue). At this point, the manufacturer should not play
don’t Sue when the competitor plays Sue. Otherwise, if he does, he will lose the game.
Part 3
The second solution was brought by a different coworker. She also created a payoff
matrix for the scenario but did some independent research to estimate the competitor's
profits in each outcome independent of the manufacturer's profits and came up with the
following payoff matrix; again, the values represent millions of dollars in annual profits.
This coworker concludes that under these circumstances, the manufacturer should sue
50% of the time and not sue the other 50% of the time, and they should expect their
competitor to do the same.
Competitor
Manufacturer Sue Don’t Sue
Sue (5, -5) (20, 10)
Don’t Sue (10, 20) (15, 15)

DELIVERABLE 07 6
7
 Use the mixed strategy algorithm to find the optimum strategy for the
manufacturer. Show all of your steps.
Solution
Assume that the manufacturer believes that the competitor will play Sue with a
probability of p.
Then,
5p + 20(1-p) = 15p + 20(1-p)
5p + 20 – 20p = 15p + 20 -20p
-15p + 20 = 20 – 5p
P =0, no optimal strategy for the manufacturer in this case.
8
 Use the mixed strategy algorithm to find the optimum strategy for the
competitor. Show all of your steps.
Solution
Assume that the competitor believes that the manufacturer will play Sue with a
probability of q.
Then,
-5q + 20(1-q) = 10q + 15 (1-q)
-5q + 20 – 20q = 10q + 15 -15q
20 – 25q = 15 – 5q
5 = 20q
5/20 = q = 0.25
Then, the optimal strategy point for the competitor is (0.25, 0.75).
9
 Do your results match those of your coworker’s? Explain why you agree
or disagree.
My results differ from those of the coworker with to the issue of suing. From the payoff
matrix, it is clear that (Sue, Sue) is a Nash equilibrium point. Neither the manufacturer
nor the competitor should break the rules at this point. As a result, the manufacturer
should not sue 50% of the time and not sue the other 50% of the time.
Part 4

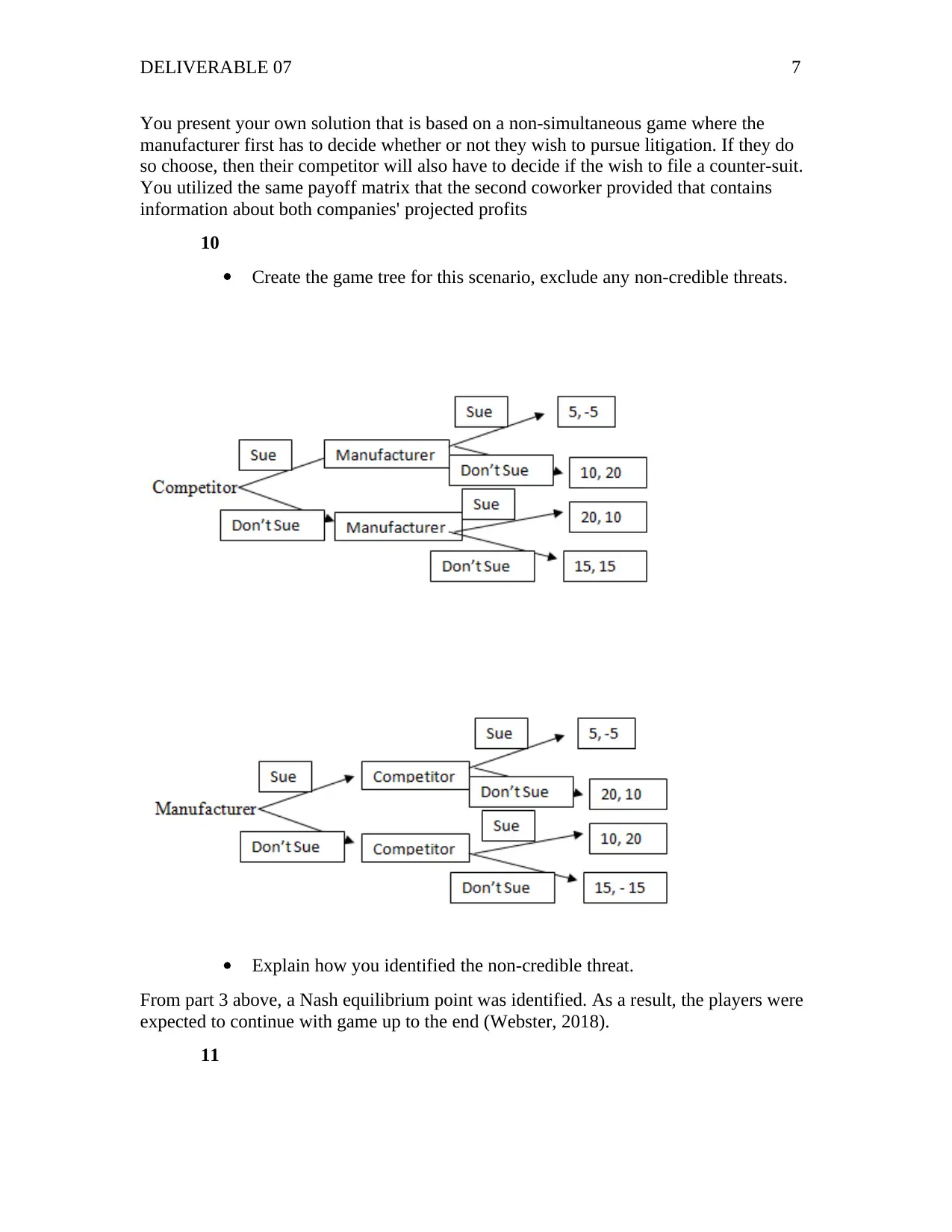
DELIVERABLE 07 7
You present your own solution that is based on a non-simultaneous game where the
manufacturer first has to decide whether or not they wish to pursue litigation. If they do
so choose, then their competitor will also have to decide if the wish to file a counter-suit.
You utilized the same payoff matrix that the second coworker provided that contains
information about both companies' projected profits
10
 Create the game tree for this scenario, exclude any non-credible threats.
 Explain how you identified the non-credible threat.
From part 3 above, a Nash equilibrium point was identified. As a result, the players were
expected to continue with game up to the end (Webster, 2018).
11

DELIVERABLE 07 8
 Perform the first step of backwards induction. Shown and explain your
work.
Manufacturer
In the first step of backward induction, I did away with the last decisions which were
made during the game.
12
 Perform the second step of backwards induction. Show and explain all
your work.
Manufacturer
In the second step of backward induction, I did away with the subsequent decisions
which were made during the game.
13
 Identify the optimum strategy for the game.
Since the payoff matrix is similar to the one that was used on part 3, the only optimal
strategy remains to be (0.25, 0.75).
Part 1 Solution
Q1.
Letting Po be the proportion of individuals to give the highest rating of customer
satisfaction, we know that the company plans to serve 60 clients in the next year.
Therefore, every client’s opportunity to approve or give the highest level of client
satisfaction will be independent of each other brought about into practice through the
application of binomial distribution using a number of trials:
5, -5
15, 15
10, 20
20, 10
5, 10
10, 15

DELIVERABLE 07 9
N (60), chances of the largest level of clients served. : Po, probability of clients giving the
lowest level of service will be given by 1-Po and X being the value of clients giving the
highest level of customer service.
Q2.
Hence, the probability distribution function of X will be given by : P(X=x) = Cnx
*Po*xqn-xo :X=0,1,2, ----n i.e. P(X=x) = C60x (Po) x (qo) 60-x : x=0, 1, 2, ---n
(Rajabioun, 2016).
Thus, qo= 1-Po.
Q3.
So, 85% of 60 = 51. Therefore, the probability of 51 or otherwise more than the
calculated 51 persons offering the largest level of client satisfaction rating will be
calculated by:
P(X=51) + P(x=52) + --+P(x=60) =∑60i=51 *60Ci (Po)i(qo)60-I (Bell, 2015)
According to the result from the analysis and calculation I best fit the position in that I
met customer satisfaction and in the coming year I will manage to satisfy 51 of the total
customers.
References
Bell, M. G. (2015). A game theory approach to measuring the performance reliability of
transports Networks. Transportation Research Part B: Methodological, 34(6),
533-545.
Rajabioun, R. (2016). Multi-Objective Optimization Using Cuckoo Optimization
Algorithm: A Game Theory Approach. International Journal of Academic
Research in Computer Engineering, 1(2), 33-43.
Webster, T. J. (2018). Introduction to Game Theory in Business And Economics.
Routledge.
Xiang, S. W., Zhang, D. J., Li, R., & Yang, Y. L. (2018). Strongly essential set of Ky
Fan's points and the stability of Nash equilibrium. Journal of Mathematical
Analysis and Applications, 459(2), 839-851.