MAE256 T2 2017 Assignment: Regression Analysis of House Sale Data
VerifiedAdded on 2020/02/24
|12
|1339
|190
Homework Assignment
AI Summary
This document presents a comprehensive solution to a statistics assignment (MAE256 T2 2017) focusing on the analysis of house sale prices. The solution begins with descriptive statistics, including the interpretation of mean, median, standard deviation, and skewness. It then explores the relationship between house prices and various factors such as size and proximity to the central business district (CBD) using correlation coefficients and scatter plots. The assignment delves into linear regression models, examining the impact of size, age, and proximity on house prices, and also incorporates dummy variables for features like pools and fireplaces. Furthermore, it investigates the use of logarithmic transformations and hypothesis testing to assess the statistical significance of different variables on house sale prices. The solution concludes with an analysis of the joint significance of the regression model through ANOVA and F-tests.

MAE256 T2 2017 –Assignment
STUDENT ID
[Pick the date]
STUDENT ID
[Pick the date]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Question 1
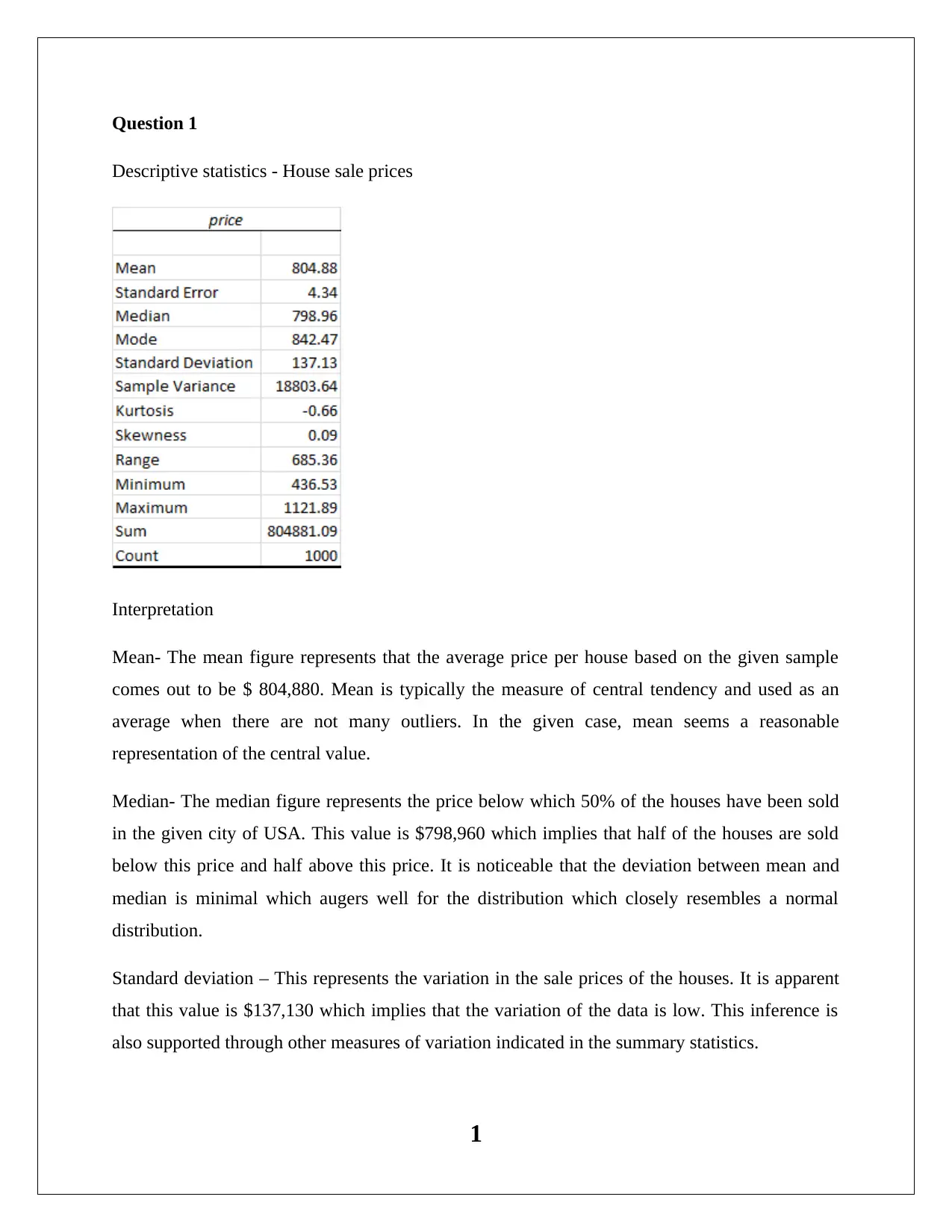
Descriptive statistics - House sale prices
Interpretation
Mean- The mean figure represents that the average price per house based on the given sample
comes out to be $ 804,880. Mean is typically the measure of central tendency and used as an
average when there are not many outliers. In the given case, mean seems a reasonable
representation of the central value.
Median- The median figure represents the price below which 50% of the houses have been sold
in the given city of USA. This value is $798,960 which implies that half of the houses are sold
below this price and half above this price. It is noticeable that the deviation between mean and
median is minimal which augers well for the distribution which closely resembles a normal
distribution.
Standard deviation – This represents the variation in the sale prices of the houses. It is apparent
that this value is $137,130 which implies that the variation of the data is low. This inference is
also supported through other measures of variation indicated in the summary statistics.
1
Descriptive statistics - House sale prices
Interpretation
Mean- The mean figure represents that the average price per house based on the given sample
comes out to be $ 804,880. Mean is typically the measure of central tendency and used as an
average when there are not many outliers. In the given case, mean seems a reasonable
representation of the central value.
Median- The median figure represents the price below which 50% of the houses have been sold
in the given city of USA. This value is $798,960 which implies that half of the houses are sold
below this price and half above this price. It is noticeable that the deviation between mean and
median is minimal which augers well for the distribution which closely resembles a normal
distribution.
Standard deviation – This represents the variation in the sale prices of the houses. It is apparent
that this value is $137,130 which implies that the variation of the data is low. This inference is
also supported through other measures of variation indicated in the summary statistics.
1

Skewness- Skew is a critical parameter which tends to be determine the shape of the distribution.
A positive skew indicates a rightward shift while a negative skew indicates a leftward shift. For
the given data, the skew is almost zero as it only 0.09 which represents a slight tail towards the
right.
Question 2
Mean = 804.88
Standard deviation = 137.13
One-standard deviation from the mean house prices:
Upper range ¿ Mean+ ( 1∗Standard deviation )
¿ 804.88+ ( 1∗137.13 )=942.007
Lower range ¿ Mean− ( 1∗Standard deviation )
¿ 804.88− ( 1∗137.13 ) =667.75
Number of houses for which the house sale prices are fall within this range (667.75 942.007) =
638
Total number of houses = 1000
Proportion of houses with the sale price within one-standard deviation from the mean house
prices ¿ 638
1000 =0.638
Question 3
Graphical representation
Sale price of houses against size of house
2
A positive skew indicates a rightward shift while a negative skew indicates a leftward shift. For
the given data, the skew is almost zero as it only 0.09 which represents a slight tail towards the
right.
Question 2
Mean = 804.88
Standard deviation = 137.13
One-standard deviation from the mean house prices:
Upper range ¿ Mean+ ( 1∗Standard deviation )
¿ 804.88+ ( 1∗137.13 )=942.007
Lower range ¿ Mean− ( 1∗Standard deviation )
¿ 804.88− ( 1∗137.13 ) =667.75
Number of houses for which the house sale prices are fall within this range (667.75 942.007) =
638
Total number of houses = 1000
Proportion of houses with the sale price within one-standard deviation from the mean house
prices ¿ 638
1000 =0.638
Question 3
Graphical representation
Sale price of houses against size of house
2
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Independent variable: Size of house
Dependent variable: Sale price of house
130.000 140.000 150.000 160.000 170.000 180.000 190.000 200.000 210.000 220.000
0.000
200.000
400.000
600.000
800.000
1000.000
1200.000
Scatter plot : Size - Price
Size (Square meters)
Price (thousands $)
Correlation coefficient = 0.59
It is apparent from the above scatter plot coupled with the correlation coefficient that there is a
positive relationship of moderate strength between the size and price of the house sold. Hence, as
a general rule if the house size increases, the price would increase not necessarily linearly and
would have some exceptions.
Sale price of houses against proximity
Independent variable: Proximity
Dependent variable: Sale price of house
3
Dependent variable: Sale price of house
130.000 140.000 150.000 160.000 170.000 180.000 190.000 200.000 210.000 220.000
0.000
200.000
400.000
600.000
800.000
1000.000
1200.000
Scatter plot : Size - Price
Size (Square meters)
Price (thousands $)
Correlation coefficient = 0.59
It is apparent from the above scatter plot coupled with the correlation coefficient that there is a
positive relationship of moderate strength between the size and price of the house sold. Hence, as
a general rule if the house size increases, the price would increase not necessarily linearly and
would have some exceptions.
Sale price of houses against proximity
Independent variable: Proximity
Dependent variable: Sale price of house
3
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

0 0.2 0.4 0.6 0.8 1 1.2
0.000
200.000
400.000
600.000
800.000
1000.000
1200.000
Scatter plot : Proximity - Price
Proximity
Price (thousands $)
Correlation coefficient = 0.73
It is apparent from the above scatter plot coupled with the correlation coefficient that there is a
positive relationship of moderate strength between the proximity to CBD and price of the house
sold. Hence, as a general rule if the house is in proximity of the CBD, the house would demand a
price premium with few exceptions.
Question 4
Linear regression model
Price=β0 +β1 ¿ β ¿2 Age+ β3 Proximity+ u
Output of regression is highlighted below by considering the variables.
Dependent variable = Price
Independent variable = Size, Age, Proximity
4
0.000
200.000
400.000
600.000
800.000
1000.000
1200.000
Scatter plot : Proximity - Price
Proximity
Price (thousands $)
Correlation coefficient = 0.73
It is apparent from the above scatter plot coupled with the correlation coefficient that there is a
positive relationship of moderate strength between the proximity to CBD and price of the house
sold. Hence, as a general rule if the house is in proximity of the CBD, the house would demand a
price premium with few exceptions.
Question 4
Linear regression model
Price=β0 +β1 ¿ β ¿2 Age+ β3 Proximity+ u
Output of regression is highlighted below by considering the variables.
Dependent variable = Price
Independent variable = Size, Age, Proximity
4
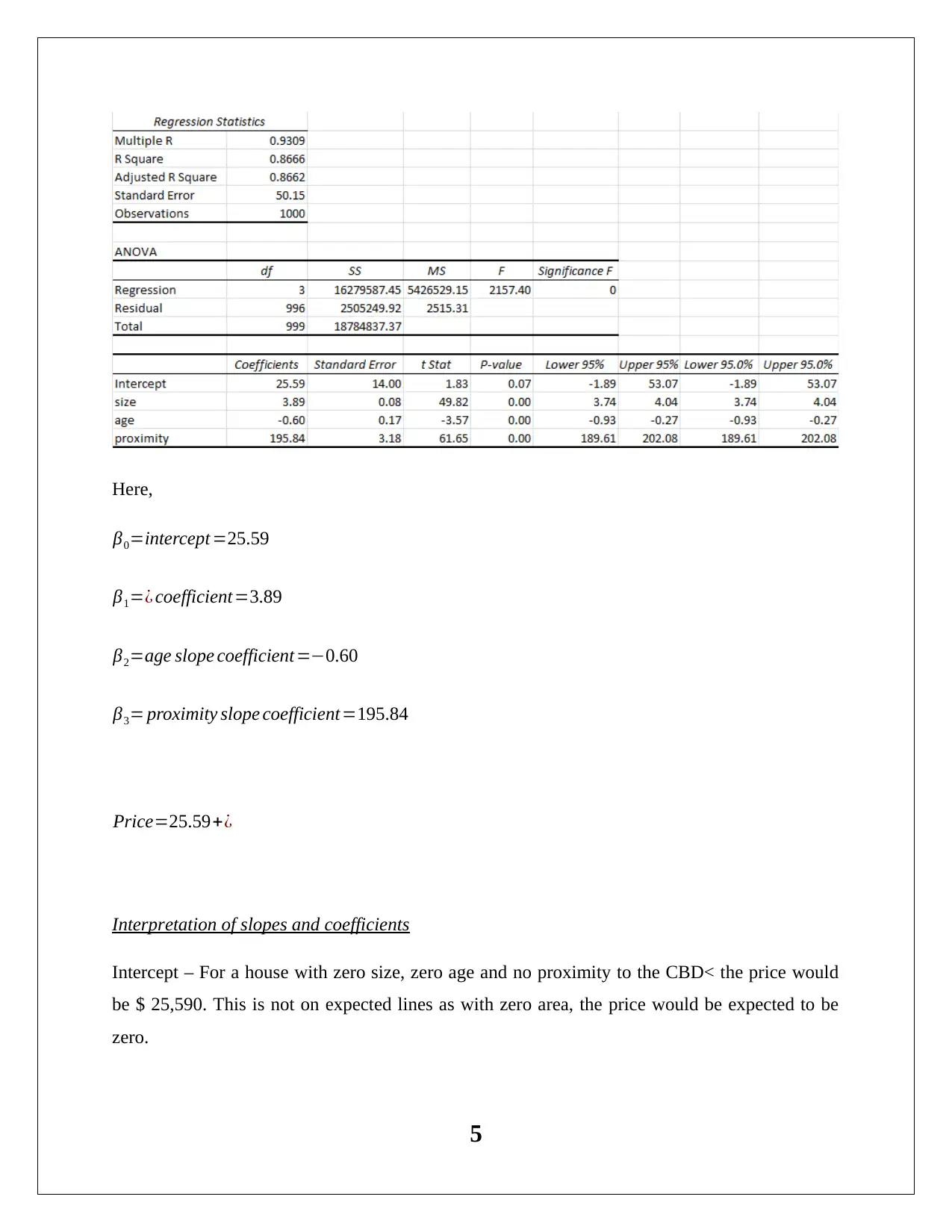
Here,
β0=intercept =25.59
β1=¿ coefficient=3.89
β2=age slope coefficient=−0.60
β3= proximity slope coefficient=195.84
Price=25.59+¿
Interpretation of slopes and coefficients
Intercept – For a house with zero size, zero age and no proximity to the CBD< the price would
be $ 25,590. This is not on expected lines as with zero area, the price would be expected to be
zero.
5
β0=intercept =25.59
β1=¿ coefficient=3.89
β2=age slope coefficient=−0.60
β3= proximity slope coefficient=195.84
Price=25.59+¿
Interpretation of slopes and coefficients
Intercept – For a house with zero size, zero age and no proximity to the CBD< the price would
be $ 25,590. This is not on expected lines as with zero area, the price would be expected to be
zero.
5
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Size Slope- As the size of the house changes by a unit area, the house price would increase by $
3,890. This is on expected lines as a positive linear relationship between area and price is
expected.
Age slope –When the age of the house increases by one year, the selling price of the house
decreases by $ 600. This is on expected lines as there is wear and tear on increase of the age of
house which reduces the market value.
Proximity Slope- For a house which is in proximity with a major business district, the selling
price tends to rise by $ 195,850. This is on expected lines as a premium is expected for houses
located near business places as people are willing to pay a premium so as to reduce the cost and
time of transportation.
Question 5
New linear regression model
Price=β0 +β1 ¿ β ¿2 Age+β3 Proximity+ β4 Pool + β3 Fireplace+u
Output of regression is highlighted below by considering the variables.
Dependent variable = Price
Independent variable = Size, Age, Proximity,
Dummy (independent variable) = Pool and Fireplace
6
3,890. This is on expected lines as a positive linear relationship between area and price is
expected.
Age slope –When the age of the house increases by one year, the selling price of the house
decreases by $ 600. This is on expected lines as there is wear and tear on increase of the age of
house which reduces the market value.
Proximity Slope- For a house which is in proximity with a major business district, the selling
price tends to rise by $ 195,850. This is on expected lines as a premium is expected for houses
located near business places as people are willing to pay a premium so as to reduce the cost and
time of transportation.
Question 5
New linear regression model
Price=β0 +β1 ¿ β ¿2 Age+β3 Proximity+ β4 Pool + β3 Fireplace+u
Output of regression is highlighted below by considering the variables.
Dependent variable = Price
Independent variable = Size, Age, Proximity,
Dummy (independent variable) = Pool and Fireplace
6
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
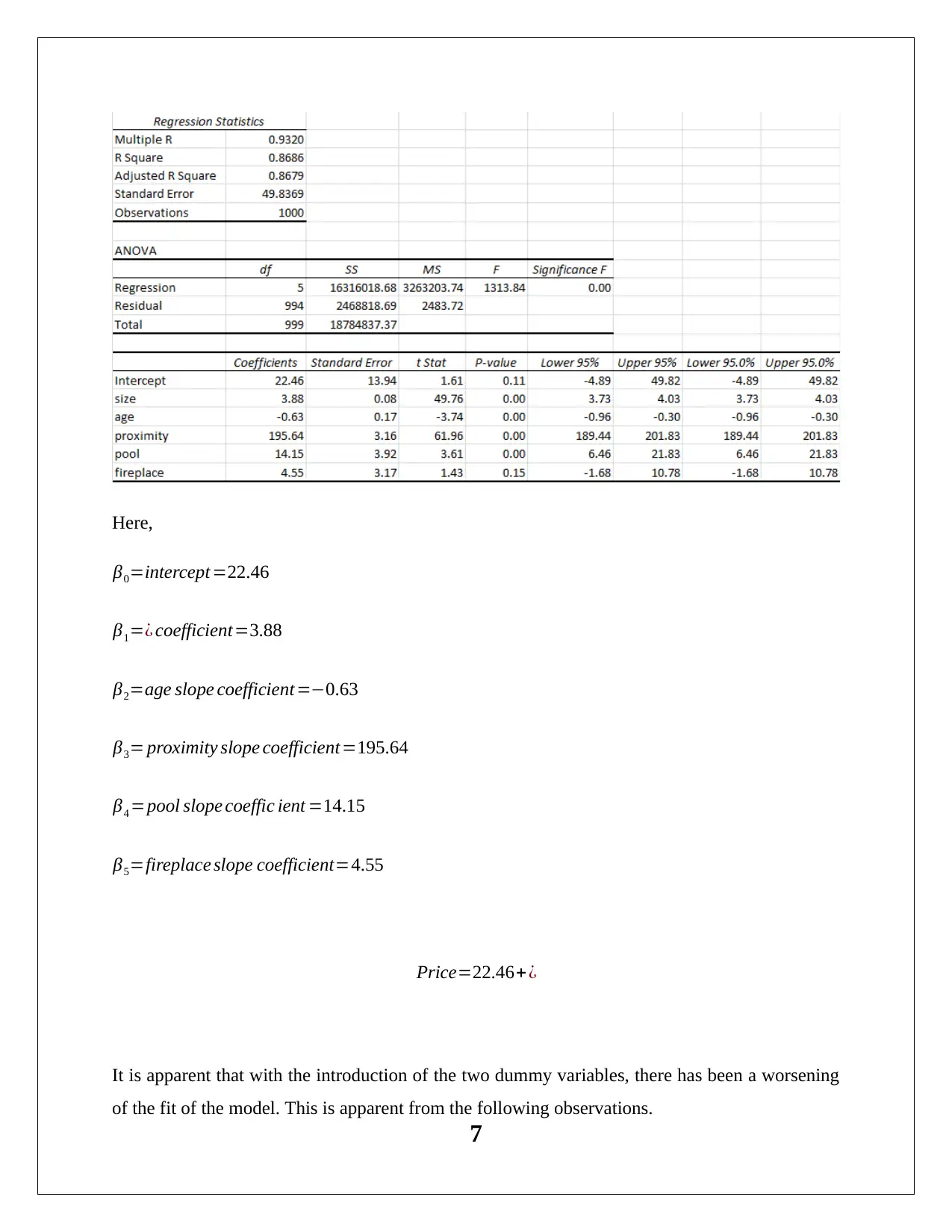
Here,
β0=intercept =22.46
β1=¿ coefficient=3.88
β2=age slope coefficient =−0.63
β3= proximity slope coefficient=195.64
β4 =pool slope coeffic ient =14.15
β5=fireplace slope coefficient=4.55
Price=22.46+¿
It is apparent that with the introduction of the two dummy variables, there has been a worsening
of the fit of the model. This is apparent from the following observations.
7
β0=intercept =22.46
β1=¿ coefficient=3.88
β2=age slope coefficient =−0.63
β3= proximity slope coefficient=195.64
β4 =pool slope coeffic ient =14.15
β5=fireplace slope coefficient=4.55
Price=22.46+¿
It is apparent that with the introduction of the two dummy variables, there has been a worsening
of the fit of the model. This is apparent from the following observations.
7

With the introduction of the two dummy variables, there has been a decline in the R2 and
adjusted R2 which represents a lowering ability of the independent variables to account
for the dependent variable movement.
Additionally, with regards to the F-test for the joint significance of the regression model,
after the introduction of the dummy variables, there has been a drop in the F value
derived which indicates a lowering the regression model significance.
Question 6
Linear regression model
By taking the natural
log (Price)=β0+ β1 log ¿
Here,
β0=intercept =2.1750
8
adjusted R2 which represents a lowering ability of the independent variables to account
for the dependent variable movement.
Additionally, with regards to the F-test for the joint significance of the regression model,
after the introduction of the dummy variables, there has been a drop in the F value
derived which indicates a lowering the regression model significance.
Question 6
Linear regression model
By taking the natural
log (Price)=β0+ β1 log ¿
Here,
β0=intercept =2.1750
8
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

β1=¿ coe fficient =0.8472
β2=age slope coefficient=−0.0009
β3= proximity slope coefficient =0.2475
β4 =pool slope coefficient =0.0186
β5=fireplace slope coefficient=0.0070
Log(Price ¿=2.1750+0.8472∗log ¿+ 0.0649
Interpretation of coefficients
β1 – It implies that if the natural log of the size of the house would increase by one unit, then the
corresponding change in natural log of the price would be 0.8472.
β4 – It implies that the natural log of the price of house tends to increase by 0.0186 when there is
presence of pool in a house. Thus, a higher price is paid for a house with a swimming pool in
comparison to one which does not have a swimming pool.
Question 7
Hypothesis testing
Null hypothesis H0 : β5=0 i.e. the slope coefficient can be assumed to be zero.
Alternative hypothesis H1 : β5 ≠ 0 i.e. the slope coefficient cannot be assumed to be zero.
From the above highlighted regression output obtained using Excel, it can be said that t statistics
for fireplace comes out to be 1.6975.
9
β2=age slope coefficient=−0.0009
β3= proximity slope coefficient =0.2475
β4 =pool slope coefficient =0.0186
β5=fireplace slope coefficient=0.0070
Log(Price ¿=2.1750+0.8472∗log ¿+ 0.0649
Interpretation of coefficients
β1 – It implies that if the natural log of the size of the house would increase by one unit, then the
corresponding change in natural log of the price would be 0.8472.
β4 – It implies that the natural log of the price of house tends to increase by 0.0186 when there is
presence of pool in a house. Thus, a higher price is paid for a house with a swimming pool in
comparison to one which does not have a swimming pool.
Question 7
Hypothesis testing
Null hypothesis H0 : β5=0 i.e. the slope coefficient can be assumed to be zero.
Alternative hypothesis H1 : β5 ≠ 0 i.e. the slope coefficient cannot be assumed to be zero.
From the above highlighted regression output obtained using Excel, it can be said that t statistics
for fireplace comes out to be 1.6975.
9
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

The corresponding p value is 0.0899.
Decision Rule: When p value is lower than level of significance, then null hypothesis would be
rejected and as a result alternative hypothesis would be accepted.
Level of significance = 1%
In this case, p value is higher than level of significance (0.089>0.01) and thus, insufficient
evidence is present to reject null hypothesis. Hence, alternative hypothesis cannot be accepted.
Therefore, it can be concluded that fireplace does not have any statistically significant influence
on the house sale prices.
Level of significance = 10%
Here, p value is lower than level of significance (0.089<1) and hence, null hypothesis would be
rejected and alternative hypothesis would be accepted. Hence, it can be concluded that fireplace
does a have statistically significant influence on the house sale prices.
Question 8
Hypothesis testing
Null hypothesis H0 : β1=β2=β3=β4= β5 =0
Alternative hypothesis H1 : at least one of the slope coefficient ≠ 0
The value of F statistics from above highlighted ANOVA table obtained as part of the regression
output from Excel is 1235.83.
The corresponding p value (Significance F) comes out to be zero (0.00).
10
Decision Rule: When p value is lower than level of significance, then null hypothesis would be
rejected and as a result alternative hypothesis would be accepted.
Level of significance = 1%
In this case, p value is higher than level of significance (0.089>0.01) and thus, insufficient
evidence is present to reject null hypothesis. Hence, alternative hypothesis cannot be accepted.
Therefore, it can be concluded that fireplace does not have any statistically significant influence
on the house sale prices.
Level of significance = 10%
Here, p value is lower than level of significance (0.089<1) and hence, null hypothesis would be
rejected and alternative hypothesis would be accepted. Hence, it can be concluded that fireplace
does a have statistically significant influence on the house sale prices.
Question 8
Hypothesis testing
Null hypothesis H0 : β1=β2=β3=β4= β5 =0
Alternative hypothesis H1 : at least one of the slope coefficient ≠ 0
The value of F statistics from above highlighted ANOVA table obtained as part of the regression
output from Excel is 1235.83.
The corresponding p value (Significance F) comes out to be zero (0.00).
10

Decision Rule: When p value is lower than level of significance. then null hypothesis would be
rejected and as a result alternative hypothesis would be accepted.
Level of significance = 5%
It is apparent that p value is lower than level of significance and thus, sufficient evidence present
to reject null hypothesis and to accept alternative hypothesis. Therefore, it would be fair to
conclude that at least one slope coefficient is significant i.e. would not be equal to zero. This
clearly highlights the joint significance of the regression model under consideration.
11
rejected and as a result alternative hypothesis would be accepted.
Level of significance = 5%
It is apparent that p value is lower than level of significance and thus, sufficient evidence present
to reject null hypothesis and to accept alternative hypothesis. Therefore, it would be fair to
conclude that at least one slope coefficient is significant i.e. would not be equal to zero. This
clearly highlights the joint significance of the regression model under consideration.
11
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 12
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





