Calculus Assignment: Differentiating Functions and Applications

This document presents a comprehensive solution to a differential calculus assignment, covering a range of topics and problem types. The assignment begins with differentiation techniques, including algebraic functions, the quotient rule, logarithmic functions, and the product rule. It then moves on to applications of calculus, such as calculating the area enclosed by curves and determining the temperature of a cooling object. The assignment also includes optimization problems, such as finding the least area of a lidless box and determining the height and radius of a cylinder with the least surface area. Each problem is solved step-by-step, demonstrating the application of calculus principles to real-world scenarios. This solution is designed to help students understand and master differential calculus concepts.

Differential Calculus

TABLE OF CONTENT
TASK 1 ...........................................................................................................................................1
A. Differentiate the algebraic function .......................................................................................1
B. Differentiating using quotient rule .........................................................................................1
C. Differentiating logarithmic function ......................................................................................2
D. Differentiating using product rule ..........................................................................................2
TASK 2 ...........................................................................................................................................3
B. Area enclosed by curves .........................................................................................................3
TASK 3............................................................................................................................................4
A. Calculating Ɵ1 .......................................................................................................................4
B.) Calculating temperature of cooling object ............................................................................5
TASK 4............................................................................................................................................6
A Least area of lidless box ..........................................................................................................6
B Height and radius of cylinder with least surface area .............................................................7

TASK 1
A. Differentiate the algebraic function
Equation linking distance and time is given by:
x = 3t + 0.5 at²
a = acceleration t = time v = velocity
a = 1.6 m/s² t = 5 seconds
Solution
Velocity (v) = Rate of change of distance = dx/dt
v = d (3t + 0.5 at² ) / dt
v = 3 + 0.5a *2t (a is constant = 1.6, as given)
v = 3 + 1.6t
at t = 5 seconds
velocity = 3 +(1.6*5) = 11 m/second
B. Differentiating using quotient rule
y= [e^(2t) ] / sin 5t
Solution
As per quotient rule:
If u and v are function of t then
du / dv = (du *v ) - (u*dv) / v² where du = du/dt and dv = dv/dt
In the given situation
u = e^(2t)
v = sin 5t
du / dt = 2e^(2t)
dv / dt = 5cos 5t
On substituting these values we get
dy = [2e^(2t) * sin 5t ] - [e^(2t) * 5cos 5t ] / (sin 5t)²
dy = e^(2t) [2sin 5t - 5cos 5t] / (sin 5t)²
1

C. Differentiating logarithmic function
y = ln [(x-2) (x+1) / (x-1) (x+3) ]
Solution
Using the formula: d (ln x) / dx = 1/x
Using the property of logarithmic functions we have:
ln (a/b) ln a – ln b
ln (ab) = ln a * ln b
Similarly for function y:
ln (x-2) (x+1) / (x-1) (x+3) = ln [(x-2) (x+1) ] - ln [(x-1) (x+3)]
It can be further simplified as = ln (x-2) + ln (x+1) - [ln (x-1) + ln (x+3)]
y = ln (x-2) + ln (x+1) - ln (x-1) - ln (x+3)
Using differentiation property we have:
dy /dx = [1 / (x-2)] + [1 / (x+1)] - [1 / (x-1)] - [1 / (x+3) ]
D. Differentiating using product rule
v = 4t sin 2t when t = 0.5 seconds
Solution
According to product rule if a and b are two functions of x then
d (ab) /dx = a'b + ab' where
a' = da /dx and b = db /dx
v = 4t sin 2t
In the given function of voltage a = t and b = sin 2t
On applying differentiation property of products we can write:
dv / dt = 4 * [ t * d (sin 2t ) + d (t) * sin 2t ] dt
dv / dt = 4 * [ t * 2 * cos 2t ] + [sin 2t ]
dv / dt = 4 * [2t cos 2t + sin 2t ]
dv / dt = 4 * [2t cos 2t + sin 2t ]
At t = 0.5 seconds
Rate of voltage change across capacitor = 4 [sin 2(0.5) + 2(0.5) cost 2(0.5)]
2

dv / dt = 4 [sin 1 + cos 1 ]
TASK 2
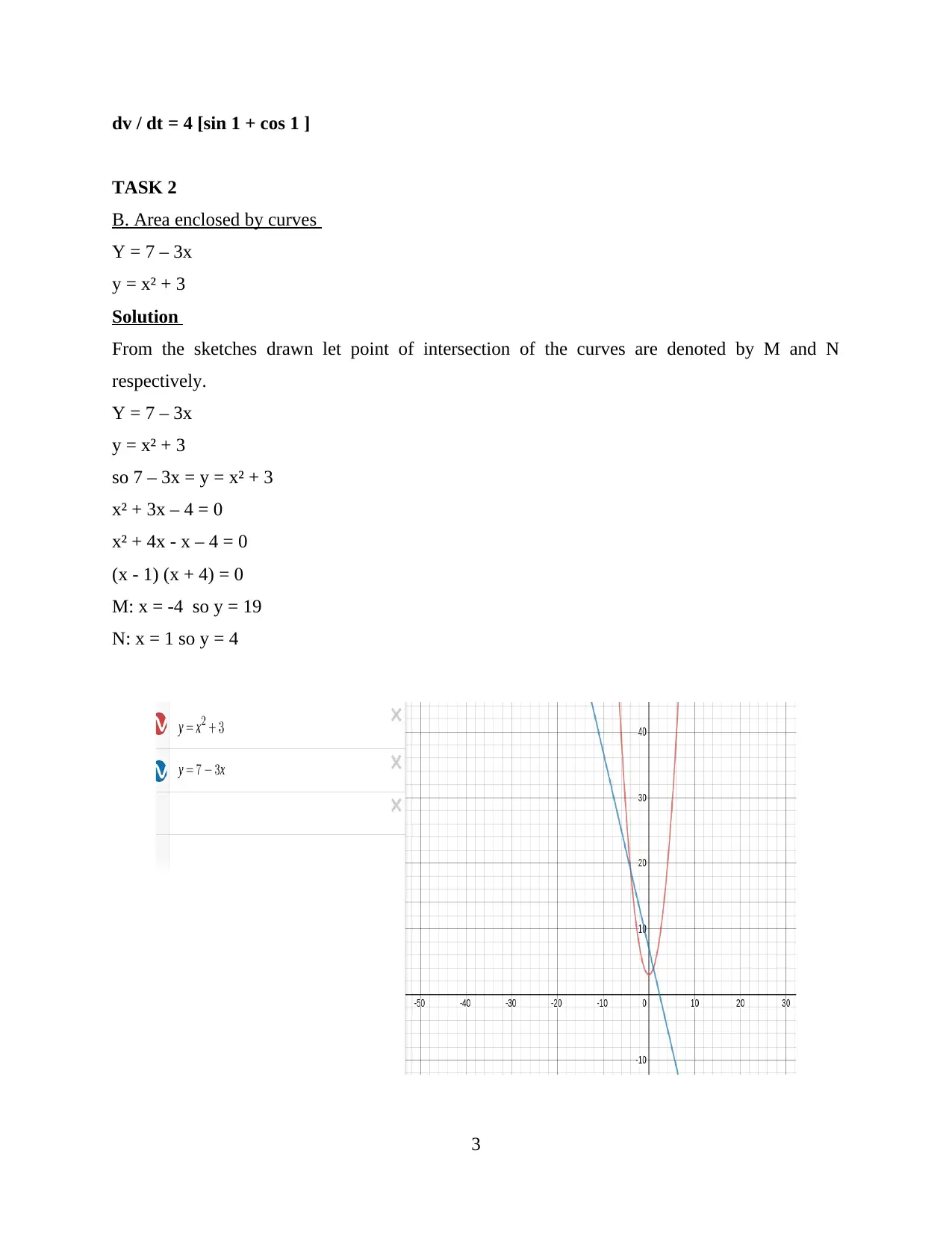
B. Area enclosed by curves
Y = 7 – 3x
y = x² + 3
Solution
From the sketches drawn let point of intersection of the curves are denoted by M and N
respectively.
Y = 7 – 3x
y = x² + 3
so 7 – 3x = y = x² + 3
x² + 3x – 4 = 0
x² + 4x - x – 4 = 0
(x - 1) (x + 4) = 0
M: x = -4 so y = 19
N: x = 1 so y = 4
3

Now we can use method of vertical strips to find the area of enclosed curves. The entire
enclosed area is divided into thin vertical strips. The width and height of strip is dx and (7 - 3x) -
(x² + 3) respectively. For calculating area it is integrated from x = -4 to x = 1.
The area dA of strip = [(7 - 3x) - (x² + 3)] dx
Enclosed area by curve = A = ∫ dA with lower and upper limits as -4 and 1 respectively
= ∫ [(7 - 3x) - (x² + 3)] dx [-4, 1]
= ∫ [4 - 3x - x² ] dx [-4, 1]
= 4x – 1.5 x² – 0.33 x³ [-4, 1]
Area enclosed = [2.17] - [-18.88] = 21.05
Area = 21.05
TASK 3
A. Calculating Ɵ1
Ɵ2 = Ɵ1 [1- e^ (-t / τ)]
Ɵ1 = final temperature (in degree Celsius)
t = time in seconds
τ = time constant
Ɵ2 = winding temperature
Solution
i) Finding Ɵ1 when Ɵ2 = 50˚ C , t = 40 seconds and τ = 34 seconds
Ɵ2 = Ɵ1 [1- e^ (-t / τ)]
On substituting values we have
50 = Ɵ1 [1- e^ (-40 / 34)]
50 = Ɵ1 [1- e^ (-1.176)]
50 = Ɵ1 [1- e^ (-1.176)]
e^ (-1.176) = 0.3085 so
50 = Ɵ1 [1- 0.3085]
50 = Ɵ1 [1- 0.3085]
4

50 = Ɵ1 [0.6915]
Ɵ1 = 72 ˚
ii) Time t when Ɵ2 = 0.5 Ɵ1
Ɵ2 = Ɵ1 [1- e^ (-t / τ)]
Ɵ2 = 0.5 Ɵ1
0.5 Ɵ1 = Ɵ1 [1- e^ (-t / τ)]
0.5 = [1- e^ (-t / τ)]
e^ (-t / τ) = 0.5
Taking logarithmic both the sides
(-t / τ) = (-0.693)
time t = 0.693 τ when Ɵ2 = 0.5 Ɵ1
B.) Calculating temperature of cooling object
Temperature (T) = 170* e ^ (-0.06t) where t = time
Solution
i) Temperature when t = 0
Rate of change of temperature = dT / dt = d [ 170* e ^ (-0.06t) ] / dt
= 170* e ^ (-0.06t) * (-0.06)
at t = 0
dT / dt = 170 * (-0.06) (e^0 = 1)
dT / dt = (at t = 0) = - 10.2
The negative rate of change indicates that the temperature declines with increasing
time period.
ii) Time taken by cooling object to reach temperature of 35 degree Celsius
T = 170* e ^ (-0.06t)
Given T = 35 degree Celsius we have
35 = 170* e ^ (-0.06t)
5

0.20588 = e ^ (-0.06t)
On taking log both the sides we have
ln (0.20588) = (-0.06t)
ln (0.20588) = - 1.580
(- 1.580 )= ( - 0.06 t )
t = 26.33 seconds
Thus it takes 26.33 seconds to reach 35 degree Celsius temperature.
TASK 4
A Least area of lidless box
Volume of box = 3.8 m
Solution
The dimensions of box are :
Length (l) = x
Width (w) = y
Height (h) = x
Volume = lwh = xy
3.8 = xy
y = 3.8 / x
The area of lidless box (A) = 2xy + 2x + 1xy = 2x + 3xy
On substituting y = 3.8 / x
A = 2x + 3x(3.8 / x ) = 2x + (11.4 /x)
On differentiating surface area we get:
dA / dx = 4x – 11.4 / (x)
Equating it to zero :
4x = 11.4 / (x)
x = (2.85 )⅓ = 1.41
so y = 3.8 / x = 1.91
Thus the dimensions of box are 1.41 * 1.91 * 1.41
6

B Height and radius of cylinder with least surface area
Volume of cylinder = 235 cm cube
Solution
Volume of cylinder = π r² h where r is radius and h is height of cylinder
235 = π r² h
h = 235 / π r²
Total surface area of cylinder (A) = 2 (π r²) + 2 π r h
= 2π r² + 2 π r ( 235 / π r² )
= 2π r² + (470 / r )
The minimum surface area with radius r > 0 we can write
dA / dr = 4π r – (470 / r² )
It will satisfy the required conditions when
4π r = (470 / r² )
Thus its only possible solution is when
r = (117.5 / π )⅓ = 3.344
h = 235 / π r² = 6.69
When r is close to zero then dA / dr < 0
When r is larger then dA / dr > 0
Thus least surface area is obtained when r = 3.344 cm and h = 6.69 cm
7

8

9

10